一种毫米波测速雷达系统的工作原理

摘要：介绍了一种毫米波测速雷达系统的工作原理，该系统采用高精度谱分析法测量外弹道弹丸速度曲线，并利用最小二乘法拟合方法推出弹丸的初速。分析了测速误差、精度与测点数、外推步长的关系。该系统将毫米波技术成功应用于火炮或枪支的内、外弹道参数的测试。通过与国外同类产品测试比对，证明该系统具有较高的测试精度。

关键词：毫米波雷达，初速，谱分析

随着武器测试技术的进步、传统的测速技术，如靶圈测试、天幕靶测试等方法因测试过程 繁琐，精度较差，已不能满足实时战地测试的需要。而毫米波测速雷达将毫米波技术成功应用于火炮或枪的内、外弹道参数的测试。毫米波测速雷达较现有各种测速雷达具有体积小、重量轻，在应用于内、外弹道的测试中工作可靠、测试简便、快速、精确、操作使用方便等特点;火炮初速值的测定还可用于对火炮初速的预测，对提高火炮的射击精度具有重要的意义。

1 测速雷达系统结构及工作原理

毫米波测速雷达系统主要由高频头［1］、预处理系统、终端系统和红外启动器等组成，其原理结构如图1所示。

毫米波振荡器产生毫米波（8mm）振荡，设其频率为f0，经隔离器加至环行器，再由天线定向辐射出去，并在空间以电磁波形式传播，当此电磁波在空间遇到目标（弹丸）时反射回来。如果目标是运动的，则反射回来的电磁波频率附加了一个与目标运动速度vr成正比 的多普勒频率fd，使反向回波频率变为f0±fd（目标临近飞行取“+” ，目标远离飞行取“%”），此回波被天线接收下来，经环行器加至混频器，在混频器中与经环行器泄漏的信号（作为本振信号）f0进行混频。混频器为非线性元件，其输出有多种和差频率，如fd，f0±fd，2f0±fd，…，等，经前置放大器选频得多普勒信号（频率为fd），再经长电缆（长50～100m）送至预处理系统的主放大器，主放大器附有自动增益控制与手动增益控制电路。手动增益用来调整放大器的总增益，自动增益控制用来增加放大器的动态范围。

内弹道测试一般不使用自动增益控制。自动增益控制只适于测试外弹道，因为外弹道测试时，为了避开枪口火焰等的干扰，应进行适当延迟才开始测试。

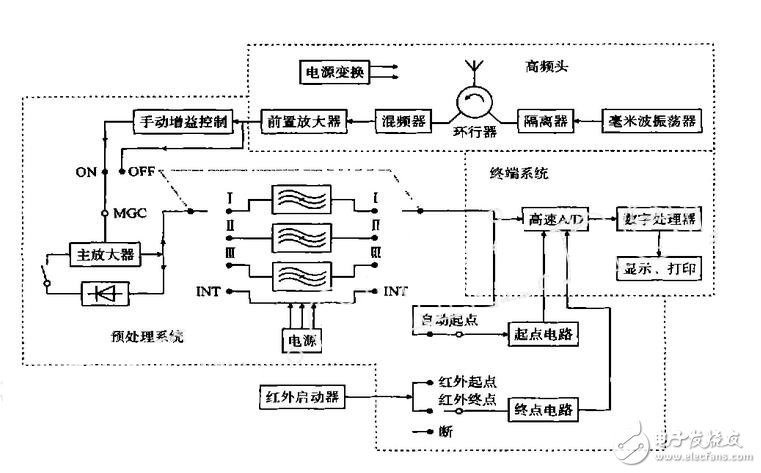
图1 毫米波测速雷达系统原理结构图

多普勒信号经放大器放大，送至带通滤波器，若进行内弹道测试将开关置于全通（INT）位置，此信号再送到终端系统的高速采样ADC，并将结果送入高速缓存区，由数字处理器计算出内弹道l2t、v2t曲线。若进行外弹道测试，则将离散信号进行32次截短，同时求出每次截短的谱，根据主谱所形成的轨迹，即可得到弹丸速度变化曲线，再根据此曲线按最小二乘法拟合，外推出外弹道初速v0，并给出v2t曲线。 起点与终点电路保证测试在正确的时间进行，并给出测试的时间基准。内弹道测试一般使用自动起点，终点信号可由红外启动器给出。在进行外弹道测试时，起点信号可以使用自动起点，也可用红外启动器信号做为起点，外弹道测试一般不设置终点信号。

2 毫米波测速雷达的测速原理

2.1 测速原理

如前所述，毫米波测速雷达的测速原理是利用电磁波在空间传播遇到运动目标时产生多普勒效应来进行的。即雷达发射的电磁波（频率为f0）遇到运动目标时所产生的回波信号，频率为f0±fd，fd为多普勒频率，它与目标径向速度vr的关系为fd=［2vr/（c+vr）］f0.其中，c为光速，一般cµvr.由此得vr=（λ0/2）fd，其中，λ0=c/f0，为发射电磁波的波长。由此可见，只要测得fd（f0和c是已知的），即可由公式求出径向速度vr。

测量fd大致有2种方法：时域法和频域法。因雷达工作环境恶劣（如枪、炮的冲击振动，火焰电离等的影响），会使接收到的多普勒信号的“背景”十分复杂，信噪比大大降低，采用传统的时域处理方法对被淹没在干扰和噪声中的多普勒信号检出或识别往往是困难的，使得测频精度明显下降。而采用频域谱分析方法，选择合适的采样频率及适当的窗口，可以大大提高测频精度和可靠性。

2.2 外推初速的基本原理

毫米波测速雷达外推初速的基本原理，是测量弹丸在外弹道起始某一段（如t1至tm）上若干点的速度，然后按外弹道规律外推出初速v0。

根据外弹道理论，在外弹道起始段，可将速度表示为v（t）=v0+αt+βt2.其中，v0是弹 丸初速，α、 β是符合系数。

将t1，t2，…，tm时刻测得的速度v1，v2，…，vm表示为vi=v0+αti+βt2 i+εi，i=1， 2，…，m，式中，εi是随机测量误差 ［2］ ，它是一个随机变量，v0、α、β是待定参量，而v0正是要求的初速。根据最小二乘法，求出一组参数^v0、^α、^β，使速度测量值的残差平方和Q= ∑ mi=1 ［vi -（^v0+^αti+^βt2i）］2 为最小。为此推导如下：

由5Q/5v0=0，5Q/5α=0，5Q/5β=0，可得：

式中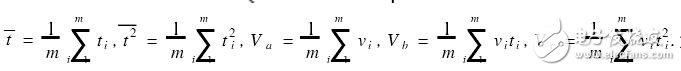，。将（1）式写成矩阵形式则为：

S^θ=B

式中，。

解方程（2），得：^θ=S -1 B。

当随机变量qi相互独立，且服从正态的N（0，σ2 ）分布时，最小二乘估计^θ将有如下优 良统计特性，即（1）^θ是θ的无偏估计;（2）^θ是θ的最小方差估计;（3）VAR（^θ）=（σ2/m）S-1.无偏性说明多次估计的统计平均接近真值。最小方差是指在各种估计中，这种 估计可以使方差达到最小，方差小意味着估计值偏离真值的程度小。因此，VAR（^θ）的大小 可以作为^θ好坏的标准。设C=S-1/m相应的^v0的偏差E（^v0-E^v0）=C11σ2 ，其中C11是矩阵C中对应的元素。为了分析计算方便，设测点间隔为等距，即t2-t1=t3-t2=… =tm-tm-1=Tz，而t1=αpTz=Ty，则矩阵S中的元素成为???? t=Z1Tz，t2 =Z2T2 z，t3 =Z3T3z，t4=Z4T4z.其中，Z1=αp+（m-1）/2，Z2=α2p+αp（m-1）+（m-1）（2m-1）/6，Z3=α3p+3α2p（m-1）/2+αp（m-1）（2m-1）/2+m（m-1）2/4，Z4=α4p+2α3p（m-1）+α2p（m-1）（2m-1）+αpm（m-1）2+（m-1）（2m-1）（3m2-3m-1）/30.根据 线性代数中矩阵求逆的方法可得：

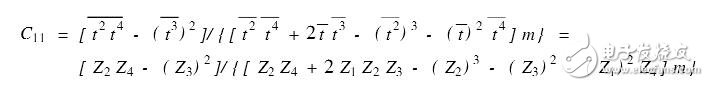
可见估计值^v0的方差E（^v0-E^v0）=C11σ2 与αp及m有关，不同的αp和m有不同的方差。方差越小越好，通常是与测量数据的误差εi的方差进行比较，因此定义η0=E［^ v0-E^v0］2/σ2 =C11为初速v0的方差压缩系数。当η0>1时，说明外推初速的误差大于测量误差;当η0=1时，说明外推初速的误差与测量误差相等;当η0<1时，说明外推初速的误差平均小于测量误差。由前面关系可知η0=C11只与外推步长αp和测量点数m有关，这样可通过选择αp和m来达到所要求的外推精度。表1给出了使η0≈1时，不同步长αp所对应的测点数m，由表可见，外推步长αp越大，则所需测点数越多。毫米波测速雷达通常取m=32.此时要使η0≤1，则可使αp≤6.例如，当测点间隔约为5ms时，则延迟时间要小于30ms才能保证外推初速的精度与测点精度相当。

如果令m=32，则可根据前述公式计算出外推步长αp与外推v0的方差压缩系数η0的关系，如表2所示。

可见，从提高外推精度的观点出发，希望αp取得小一些（m已定），即延迟时间t1取得短一些，但t1也不可取得过短，否则无法避开膛口火焰、冲击振动的影响。根据实际测试需要，测速雷达可以安装在火炮的摇架上，雷达的观测方向与弹丸飞行方向一致，不存在角度修正。若架设在三角架上，此时雷达的观测方向与弹丸飞行方向有一定夹角γ，雷达所测速度，只是弹丸速度在γ方向的分速度，如图2所示。为减小这一测速误差，应尽量减小D，增大 L（即增大延迟时间t1）。

毫米波测速雷达为减小这一测速误差，一般取D=0.2～0.5m，L≥25D，此时有L ≈v0t1，v′0=v0/cosγ，γ=arctan（D/L），测速的相对误差σ=（v0-v′0）/v0=1-v′0/v0= 1-v0cosγ/v0=1-cosγ。例如，测试某式7.62mm步枪，可取D=0.2m，设初速v0=760m/s，则要求t1≥L/v0≥25×0.2/760=6158ms.取t1=7ms，此时测速精度为σ=1-cos［arctan（D/L）］=1-cos{arctan［012/（760×7×10-3）］}=711×10-4。

3 结束语

毫米波测速雷达现已成功应用于国内多家靶场，其测试精度达0.1%.经与国外582雷达及丹麦的伟伯尔雷达进行比对试验，测试结果一致。 在实际应用中，发现数据采集的延迟时间参数（外推步长）对测试的初速值精度的影响与理论分析一致，但外推步长的设定也与其它很多因数有关，如它随不同的弹种、环境温度等而变化。对于延迟时间选定的机理和有关理论还需进一步研究或通过大量实验论证，以进一步提高测试精度。

参考文献：

1 孟庆鼐,陆士良.八毫米微带多普勒雷达收发前端.合肥工业大学学报,1995,18（3）:98-101

2 楼宇希著,雷达精度分析.北京:国防工业出版社,1979