这是一篇关于通信的小故事,握着手机的你请不要太过严肃地把这篇文章当作枯燥的学术文章,这只能算是一个通信出身的孩子对生活的一点新的理解,不需要太高的阅读门槛,只希望屏幕前的你可以通过这个小故事对这个世界有一个新的理解。
在接触通信理论之前,很多问题一度让我困惑不解。我不明白为什么有些掏心掏肺的沟通最后产生了误解,也不明白为什么会有一些稀奇古怪让人想把自己头发拔光的规定或法律,更不懂为什么一些表面合理的计划最后却落得漏洞百出。直到几年前的一天,当我对着黑板抄着笔记,一个原本熟悉得不能再熟悉的词突然在我脑中闪起了光芒,一下子解答了很多曾经的问题——这个词就叫做信噪比。
信噪比(Signal-to-noise ratio),简称SNR,这三个字经常会出现在各种文章、文献、产品说明书中,然而它并不是简单的一个通信专业名词,而是一个无处不在的衡量天枰。它可以衡量一个人的生活状态、工作状态,可以衡量爱人间、朋友间的情感交流效率,同样也可以衡量一个社区或是一个系统的运行状态。
先不谈公式和法则,我们来看一个综艺栏目里的小游戏。游戏的规则很简单,几个人排着队,最后一个人根据得到的单词画出一幅图,然后前一个人看这幅图再画出新的图,这个过程一直向前传递。最终,最前面的人根据最后一张图猜出最开始的单词,整个过程不能交谈。那么这样的游戏最后会闹出什么样的笑话呢?
第一个人拿到的问题是:老虎。虽然画工不佳,但是他也基本画出了一个野兽的造型
然而之后的三个人脑洞大开,分别画出了如下三幅图:
最后一个人看到第四幅画一脸茫然,只能胡乱猜了一个自己都不大相信的答案——兔子。
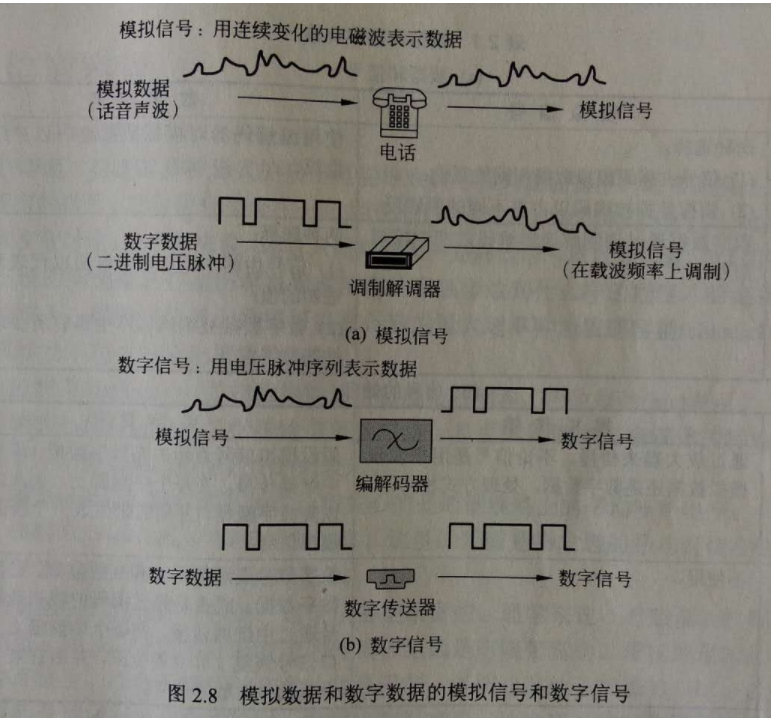
这个游戏里实际包含了一个通信过程的大部分内容,老虎是信息,图画是编码,识图是解码。而最后信息错误的传达则是因为编码中混入了人为的噪声。
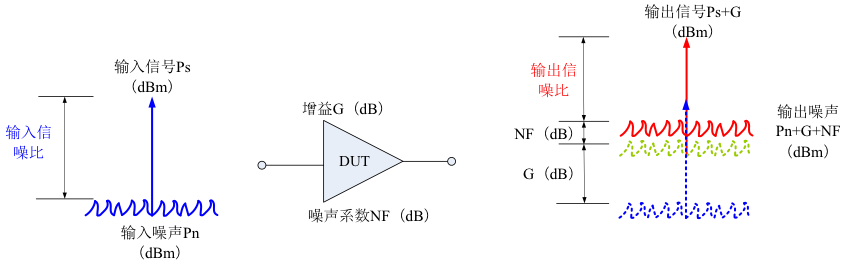
信息与噪声这两个重要的概念,无时不刻不出现在我们的生活中。我们说的每一句话,每一个动作和表情都是信息,而干扰真实信息的就是噪声。信噪比,就是我们需要的信号能量与噪声能量的比值。(实际应该是功率的比值)而这个游戏实际还验证了一个噪声系数的级联公式:一个通信系统中,越靠近前级的部分,对最终传输质量的影响越大,具体我们后面再谈。
所有的通信技术,实际上都只有一个目的——提高信噪比。对于通信人,最大的敌人,就是噪声。通信工程师们的首要任务,就是找到一个空间,并保证这个空间尽可能小的被噪声影响。这个空间可以是一个实际的物理空间,也可以是一个频率空间,或者一个概率空间,又或者是其他的数学空间。但是首先,我们来看一下到底噪声是如何影响信号传输的。
在一个没有噪声的空间里,理论上我可以把全宇宙所有的信息瞬间传送。打个比方,我有一部电影,电影大小3Gb,我们把这30亿个二进制字节变成十进制,再把这个数字前面加上小数点变成小数,比如0.12345……,然后我传送给你一个直流电信号,强度就是0.12345……伏,那么你接到信号,再把这个时间长度转化为二进制,那么你就获得了这部电影的全部信息。但是实际中,有可能存在一个随机的噪声,使得电信号强度随机增加0.001-0.002伏。这使得小数点后第三位的数字完全变得随机且不可用,能保证正确的数字只有前两位,别说一部电影,连一个汉字都发送不了。
记得中学时讲到牛一律时,老师总会举例:如果一个小车在一个没有阻力的木板上滑行,那么它的速度就永远不会改变。之余通信,噪声就是阻力。如果存在一个没有噪声的世界,我们便再也不需要抱怨手机的信号不好,家里的网速太慢,空间科学家们也可以毫无困难的控制任何一个航天器。然而现实是残酷的,噪声无处不在,我们只好尽可能提高发送信号的能量,来保证更高的通信质量。简单来说提升通信的信噪比。比如刚才的例子,如果我们将信号强度增加10倍,变为1.2345……伏,那么我们就多了一位数字可以用来传输。
噪声让人无奈的地方来自它的随机性,如果是一个确定的附加干扰,那么我们只要测量并在原信号中减去就好了,然而噪声并不是确定的,并且随机性同时体现在了空间性和时间性上,因此在衡量噪声功率时我们使用的只能是一个概率分布的方差。幸而在实际中,这个随机性并不均匀,比如在这个空间强一点,其他空间弱一点,在这个频率强一点,在其他频率弱一点。明朝那些事里有一句话:你可以骗一部分人一辈子,也可以骗所有人一段时间,但你无法骗所有人所有的时间。因为随机的不能均匀,让我们有了挑战噪声的机会。一定存在一个空间它对于我们需要的通信条件会有更弱的干扰,那就是我们要找的。
现在来看看前文提到的空间。究竟哪些空间可以用来尽可能减少噪声的干扰呢? 先说最普通的物理空间,通过铺设光纤或者电缆,我们可以让电信号在一个受到保护的环境中传输,但是成本太高且无法做到移动传输。
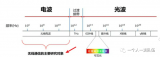
然后是频率空间,通信在频率信道的选择中更倾向选择干扰较低的信道,下图是大气层对于电磁波吸收程度的频率图:
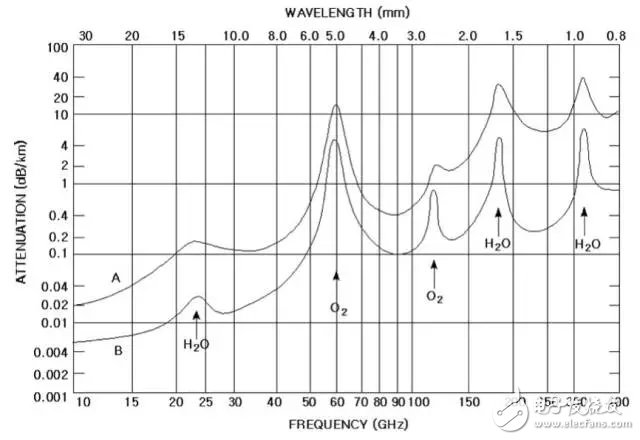
可以看到在左侧低频区,大气对电磁波的干扰要远远低于高频,所以我们将左侧的频率空间更多地留给远距离无线通信。而在中间60GHz有一个明显的峰值,我们就留给室内的短距离通信,也正是Wifi通信802.11ad协议所使用的频段。
再然后是概率空间,如果我们对噪声的随机分布足够了解,那么我们就可以通过长时间多次传输使得噪声在时间上的累加趋近于零。或是选择那些噪声概率分布更低的数值区域进行传输。在某种程度上,码分复用技术也算是其中之一。
至于其他更多的数学空间很难用笼统的语言来概括,总归一句话,通信工程师们总是在不断去寻找一个更加纯净、信噪比可以更高的空间进行信号的传输。最后得到的通信技术手段是资金、通信环境、项目要求等等多种因素妥协的结果。
现在我们把思维扩展的广一点,看看除了通信方向,现实生活中我们有哪些与信噪比息息相关。
回过头看看最初的那个游戏,信息在一次次传递中不断被模糊、扭曲,甚至造成错误的解读。噪声系数级联公式告诉我们,在一个信息逐级传输的过程中,每次信噪比都会降低,每一级的信噪比都与前几级有关。对于一个企业的管理,实际就是一个信息逐级传递的过程。假设你是一个企业的管理者,你会经常发现管理中的力不从心,你下达的任务和指标最后往往无法被准确准时的执行,并且在执行的过程中部门间的协调也总是不尽如人意。这里面最核心的原因就是你向下传达的信息被每一次传递的时候都会出现一定的理解误差,而且企业的规模越大,部门等级越多,你的管理意图就会被更多的错误解读。因此越是庞大的企业,他的管理规定就越是繁琐与严格,因为规章制度是纠正信息传递偏差的有效手段。
在通信中,有一种纠错方法叫做校验,简单来说就是用额外的信息去验证原始信息的准确性。比如最简单的奇偶校验方法:额外发送一个数字,这个数字表示原始信息中有奇数个零还是偶数个零。额外发送的信息越多,对原始信息的校验就更加准确,但是也使得需要发送的数据更长,数据传输效率更低。校验信息占全部信息的比例称为冗余度,当然在其他领域,冗余度同时可以表示系统在部分出错时继续完成任务的能力。
因此,并不是更多校验就会达到更好的执行能力,过多的冗余将为系统增加额外的成本,这就比如上班打卡制度,将行政成本分摊到了所有员工身上。
一个小企业尚且如此,对于国家来说,法律的制定则更加复杂。它必须保证一个百万级数量的读者在面对法律时可以得到同样的解读,因此我们看到的法律条款往往晦涩难懂,正是因为它必须尽可能的保证信息传递的精确性以及相互间的自洽性。
在人际交往中,很多误会、猜疑乃至纠纷的诞生恰恰是源于信息表达的不准确性。人类的语言是一个效率很低且容错率很低的传播方式,传播速度大约每秒1-10比特。眼前闪过一秒的画面,用语言可能要几分钟才能描述出来一个大概。想来让人有些遗憾,即使一个人从学会说话开始就一刻不停地把内心的感受说出来,到他死亡,也只能最多说出25Gb的信息,这甚至还不如一块优盘大。人的孤独可能在一开始就写进了基因里。
但是不是说一个信息越精确越好呢?是不是信噪比越高越好呢?
有时不然,有时在人与人之间的沟通中,一个模糊的信息比准确的信息往往能得到更好的效果。比如含糊其辞的外交辞令,给人的第一感觉是废话连篇,但其中却包含着大的哲学。
比如一个经典的笑话:“我国承诺不首先使用核武器”也可以诙谐地理解为我国承诺一定先使用常规武器之后再使用核武器。
又或者对一个人的劝谏,直截了当的指出对方的问题可能会伤到对方的自尊,并起到适得其反的作用。而模糊的无心之谈反而能点明一个人去反省自己。
究其原因,是因为在某种情况下,“不表态”这一行为本身也可以传达很大的信息量,而我们希望通过一种模糊的表态来尽可能减少传达给对方的信息进而保护自己。试想一下,当有人质问你:“你是不是撒谎了?”如果选择沉默,那对方会如何理解呢?
林林总总说了很多,这篇文章是我几年来整理的一些细碎观点的整合,有时想想会觉得庆幸,如果没有接触到通信理论,我可能不会用这样的眼睛去审视自己生活的世界。人活着终究会想要一个解释,这个解释未必是正确的,但是至少需要是自洽的。
 电子发烧友App
电子发烧友App




















































评论