详解随机射频干扰的抑制算法

1、引言

冲激信号（Impulse signa1）是一种脉宽极窄的脉冲信号，它同时具有低频谱分量和极大相对带宽（相对带宽77常接近100%）的优点。冲激雷达是一种超宽带（UWB）雷达，在UWB-SAR，表层穿透雷达（SPR），探测隐蔽目标的雷达中有着广泛的应用。由于其低频特性，采用这一信号的雷达系统有利于进行穿透探测，同时大的信号带宽可获得高距离分辨力（厘米级的距离分辨率）、合成孔径原理又可获得高的方位分辨率，从而能够进行高分辨成像。另外，冲激信号可以激励出丰富的目标谐波响应分量，故在探测隐身目标以及目标识别方面也有着重要的应用价值。但是冲激雷达常工作于100~1500MHz频段，存在着与这一波段密布的广播、电视和各类通信系统频谱共用的电磁兼容性（EMC）问题。这些系统的信号混合在冲激回波信号中，对冲激雷达系统形成严重的射频干扰（Radio Frequency Interference，RFI）。

通常，RFI的功率很高，它的存在降低了系统的性能，甚至造成接收机的饱和而无法正常工作。目前，RFI的抑制已经是超宽带雷达系统在诸多应用中的关键技术之一。现在已有的RFI抑制算法包括两大类，即参数法和非参数法，主要有正弦信号对消法、频域陷波法等。它们都是针对频点和带宽都有严格限定和确知的广播电台、电视干扰的，RFI的窄带性和稳定性是这两种算法的前提。正弦信号对消法抑制精度较高但模型和运算复杂，稳健性差；频域陷波算法结构简单、运算量小但没有自适应性。而移动通信设备所产生的RFI具有频点的随机性，不满足上述算法中RFI稳定性的前提。

本文针对脉冲体制的超宽带地表穿透雷达（UWB-SPR） 提出两种在时域中抑制随机射频干扰的滤波方法：波形平均法和中值滤波法，它们属于非参数法。本文第1节对特定频段的随机性RFI进行分析；第2节提出两种算法；第3节对实测的数据进行处理，并根据处理结果对两种算法的性能进行了比较和评估；最后给出了结论。

2、随机射频干扰问题的分析

UWB-SPR一般工作于100~1500MHz频段，常用来获取地下未知目标的信息，目前广泛应用于地质勘探、考古，城市建设、交通、军事等部门。在对机场、高速公路和建筑等城市中物体进行探测时，SPR常处于很复杂的电融干扰环境中容易受到多种射频的干扰，所在雷达信号或数据处理之前，需要对回波数据进行射频干扰抑制的预处理。

目前，UWB-SPR所利用的电磁波，其中心频率多在1GHz左右，3dB处带宽约为1GHz。显然，此频带范围覆盖了GSM 移动通信、电视、GPS、专用的行业通讯等的频段，其中GSM设备的发射和接收信号构成了UWB-SPR冲激回波的主要RFI。这种RFI的功率较高，比如，近距离的手机信号源对UWB-SPR，接收机的干扰功率可达7dBmW ，甚至更高，见图1（a）；该图显示了RFI在10-2500MHz范围的分布，其中，最高谱峰（902MHz，7.17dBm）为GSM 移动通信干扰、第2谱峰（91MHz-18.67dBm）和第3谱峰都为调频广播干扰、其它各谱峰为电视干扰。图1所采用的接收天线是TEM 加脊天线，带宽为2.5GHz左右。另外，RFI在回波信号频谱中表现为带宽很窄的尖峰，在时域SAR图像中则为无规则的亮线或亮斑；这些干扰将对系统的后续信号与数据处理，如分层和成像、目标分类带来很大的影响。

（a）10-2500MHz频谱 （b）GSM信号频谱

图1、RFI的频谱图

RFI的基本性质如下：

（1）由于无线电管理委员会对广播和电视信号的频点和带宽都有严格的限定。所以广播电台和电视所产生RFI在时间和频率上是稳定、确知的。

（2）无线电管理委员会对于GSM 的频段也有严格限定，但GSM 在限定的频段内采用动态信道分配方法（DCA），即系统根据当前的业务负载和干扰情况，动态地将频段内的随机信道（频率和时隙）分配给所需用户。因此，就单个GSM手机而言，其发射和接收信号在时间上是随机的，见图2（a）和图3（a）；频率上，在某一频段内也呈现随机性，见图1（b），该图显示了GSM 手机发射信号的频点在875~925MHz频段范围内的随机分布，峰值带宽随机出现；这种在时间和频率上的随机性和广播电台、电视的射频干扰在时间和频率上的相对稳定性是截然不同的。若对GSM的随机射频干扰采用上述的正弦信号对消法、频域陷波方法。就需要复杂的建模和大量的运算以自适应于GSM 射频干扰在时间和频率上的随机性。显然。对实时性很强的UWB-SPR，上述方法都不适用。

本文研究的重点是随机性RFI抑制。下面提出两种在时域中抑制GSM 随机射频干扰的滤波方法：波形平均法和中值滤波法。

3、随机射频干扰的抑制算法

3.1、波形平均算法

考虑到RFI的存在，UWB-SPR接受信号经采样后可写为如下形式：

x（n）=s（n）+r（n）+ θ（n），n=0，…，N-1 （1）

式中 x（n）为UWB-SPR的接收信号，s（n）为目标回波信号，包括探测介质的直接反射波和介质中目标的散射回波；r（n）为RFI信号，由于考虑到波段的选择与干扰功率，在本文以下的算法中不再考虑广播电台和电视等确定性的RFI，r（n）仅被看作是GSM 的随机射频干扰；θ（n）为其它类的噪声，包括系统热噪声等，它们都具有白噪声特性；N 表示一个时窗的总采样点数。由于r（n）和θ（n）都具有随机性，将这两个随机噪声合写为r0（n），可将UWB-SPR接收信号的模型简化为

x（n）=s（n）+ r0（n），n=0，…，N-1 （2）

　　式（2）中s（n）是确定性信号回波，而r0（n）是随机信号。在上述模型中随机信号r0（n）的均值为零，从而可以利用波形平均的方法对x（n）进行滤波。该方法满足MSE准则，即先对x（n）进行相干叠加，再对叠加的结果求平均，来消除x（n）中的随机性信号r0（n），而保留目标的回波信号s（n），表达式如下：

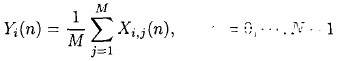　　 （3）

　　式中Xi，j（n）为在每一测量位置重复测量M 次的SPR二维剖面数据，i是测量位置的序号，通常称为道数，j是重复测量的序号；Yi（n）是经波形平均输出的UWB-SPR二维剖面数据。式（3）处理结果的误差e（n）满足MSE准则，即

　　 （4）

　　式（3）适用于系统重复频率较高时，在每道测量中做平均处理，而不是对道间数据的平均处理，这是因为SPR的回波信号随着道而变化，道间数据的平均运算将降低回波信号的能量。

　　3.2、中值滤波算法

　　中值滤波算法是对一窗口内所有数据按幅值大小进行排序，取排序后序列的中间值作为原窗口中心数据的幅值；只要选取一个有效的窗口宽度，就可以对UWB-SPR二维的剖面数据序列组，进行平滑处理，消除序列中的异常部分，抑制掉峰值噪声。中值滤波尤其适用于脉冲噪声的抑制；而GSM 的随机射频干扰信号具有窄脉冲的特性，可用中值滤波的方法有效去除回波信号中的异常部分，且能较好地保护原始回波信号。中值滤波器具有低通滤波的特性，窗口的选取有较大的影响，要保证完全去除窄带脉冲干扰，中值滤波器数据窗的宽度必须大于脉冲干扰时宽τ的2倍。窗口宽度太小，噪声抑制不彻底；窗口宽度太大，运算量较大，影响处理速度。

　　中值滤波算法的表达式为

　　Y（i，n）=med（X（i+k，n），k∈［-M，M］），n=0，…，N-1 （5）

　　式中X（i，n）为UWB-SPR二维剖面数据，n是表示深度的采样时间变量，N是一道测量的最大采样点数，i是道数，imax=D，i+k是中值滤波窗内所含道数的序号，Y（i，n）是经中值滤波输出的UWB-SPR二维剖面数据，2M +1是中值滤波数据窗的宽度，med表示对窗内的数据排序且取中值。D道数据的完整处理算法

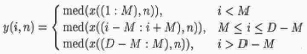　　 （6）

　　4、实测处理结果和算法性能评估

　　本实验采用一实验性SPR系统，系统发射机的中心频率为1GHz，3dB处带宽约为1GHz，信号的时宽在0.4ns左右，所选用采样时窗2Ons，每道采样512点；探测媒质为分层的混凝土路面（有沥青层和混凝土层），探测深度为0.6m左右；射频干扰信号是离天线10cm距离内两个GSM手机呼叫时的发射、接收信号，由于GSM 手机离天线距离较近，天线接收的手机信号功率远大于广播和电视信号的功率。所以可以忽略空间中所存在的其它随机性RFI。在此处手机天线处于SPR天线的近场区，由于手机天线尺寸较小且功率远小于SPR天线的功率，而且SPR在手机干扰下所接受的信号基本稳定，故本实验忽略两个天线的近场效应，此忽略不影响本文算法处理的结果。

　　4.1、两种算法的处理结果

　　为完成波形平均，需要在每一道进行重复测量和采样。该系统重复额率为100kHz。天线在每道有效停留时间内，由触发脉冲为系统产生一个M次重复测量的时隙。根据算法性能和波形平均次数的关系（见图4），以及系统的存储空间和运算速度等的要求，设定重复测量100O次，即M =1000，N=512，则波形平均的结果为

　　 （7）

　　算法的计算结果见图2。图2（a）显示了每一道数据中都随机出现射频干扰的尖峰；图2（b）是平均后的结果。各道的尖峰干扰已被消除。

　　

　　（a）波形平均前的数据图 （b）波形平均后的数据图

　　图2、波形平均前后的数据图

　　中值滤波不需要重复测量，它的关键在于中值滤波器长度的选择，这将直接影响着数据处理的效果和处理的速度。本实测处理中采用的中值滤波器长度2M +l=51，相当于1.1ns，满足M 》τ；总测量道数为D=166。每道采样点数N=512。具体计算过程如下：

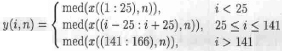　　 （8）

　　算法的计算结果见图3，图3（a）中的尖峰是GSM所产生的随机性射频干扰，显然，干扰的分布是随机的，图3（b）是中值滤波的结果，图中这种随机的RFI已经被消除。

　　

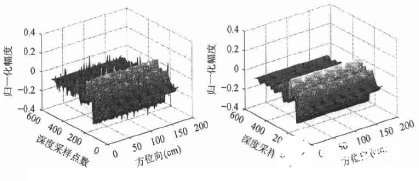
　　（a）中值滤波前的数据图 （b）中值滤波后的数据图

　　图3、中值滤波前后的数据图

　　4.2、算法的性能评估

　　4.2.1、干扰能量抑制比（IESR）

　　在抑制过程中，将RFI被对消的能量与SPR接收信号中RFI能量的比值，定义为IESR。它表示算法对RFI抑制的整体效果。由式（2）的模型，设接收信号为x（n）（n =0，…，N-1），s（n）为目标回波信号，随机噪声为r（n）；抑制RFI后的输出信号为y（n），残余随机噪声为 r’（n），则干扰能量抑制比为

　　 （9）

　　波形平均的干扰能量抑制比为IESR：97.496% 中值滤波的干扰能量抑制比IESR=99.672% 。图4给出了波形平均算法的IESR与算法平均次数M的相对应关系，可见随M 的增大，IESR逐渐提高，但在M 》10O时，IESR基本上保持不变，所以再增加波形平均的次数，算法的IESR没有明显提高。

　　

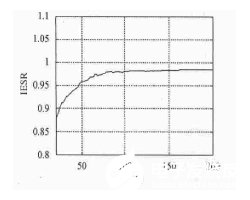
　　图4、波形平均的IESR与平均次数M 的关系

　　4.2.2、且标回波信号归一化的均方误差（NMSE）

　　IESR反映了随机RFI抑制过程中，RFI被抑制的程度，但没有考虑算法对SPR 目标回波信号所造成的失真。现定义目标回波信号的NMSE来量化RFI的抑制对目标回波产生的影响，归一化的均方误差为

　　 （10）

　　式中s（n），s’（n）分别是RFI抑制前后目标的回波信号，s（n）通常很难得到完整的解析式，所以式（10）是NMSE的理论计算式。在实际的计算过程，用屏蔽掉随机RFI的接收回波，来作为s（n）代入计算。显然，NMSE越小，RFI的抑制对目标回波信号的影响越小，即信号的保真度越高。

　　4.2.3 、RFI抑制前后的SCR

　　RFI抑制之前的SCR1

　　 （11）

　　RFI抑制之后的SCR2

　　 （12）

　　综合上述3项性能指标，对波形平均算法、中值滤波算法和频域陷波算法进行评定，见表1，其中处理增益△SCR=SCR2-SCR1，表明在RFI抑制的同时，算法对其它随机噪声抑制也有较好的效果。

　　表1、3种RFI抑制算法性能评估表

　　

　　从表1中可以看出中值滤波算法的性能最优良，它具有较高的RFI抑制能力，且能很好地保留目标的回波信号，信号扭曲度最小，NMSE仅为-38.241dB；而且在RFI抑制的同时，能大幅度地提高目标信号的信杂比，处理增益达到31.8414dB。波形平均算法的性能比中值滤波算法稍差一些；而频域陷波算法的性能最差，对于随机性的RFI，其性能远不及前两种算法，基本上不能有效去除。

　　5、结束语

　　本文在时域用波形平均和中值滤波的方法，对UWB-SPR回波信号中由GSM 移动通信设备所产生的随机射频干扰进行了抑制，给出了波形平均和中值滤波的具体算法，用实测数据进行了验证，结果表明波形平均和中值滤波都能有效快速地抑制随机性的射频干扰，其中中值滤波算法性能最优良。

　　作者：李禹、粟毅、黄春琳、高守传