射频接口和电路的特性 - 全文

射频电路（RF circuit）的许多特殊特性，很难用简短的几句话来说明，也无法使用传统的模拟仿真软件来分析，譬如SPICE。不过，目前市面上有一些EDA软件具有谐波平衡（harmonic balance）、投射法（shooting method）….等复杂的算法，可以快速和准确地仿真射频电路。但在学习这些EDA软件之前，必须先了解射频电路的特性，尤其要了解一些专有名词和物理现象的意义，因为这是射频工程的基础知识。

射频的界面

无线发射器和接收器在概念上，可分为基频与射频两个部份。基频包含发射器的输入讯号之频率范围，也包含接收器的输出讯号之频率范围。基频的频宽决定了数据在系统中可流动的基本速率。基频是用来改善资料流的可靠度，并在特定的数据传输率之下，减少发射器施加在传输媒体（transmission medium）的负荷。因此，设计基频电路时，需要大量的讯号处理工程知识。发射器的射频电路能将已处理过的基频讯号转换、升频至指定的频道中，并将此讯号注入至传输媒体中。相反的，接收器的射频电路能自传输媒体中取得讯号，并转换、降频成基频。

发射器有两个主要的设计目标：第一是它们必须尽可能在消耗最少功率的情况下，发射特定的功率。第二是它们不能干扰相邻频道内的收发机之正常运作。就接收器而言，有三个主要的设计目标：首先，它们必须准确地还原小讯号；第二，它们必须能去除期望频道以外的干扰讯号；最后一点与发射器一样，它们消耗的功率必须很小。

小的期望讯号

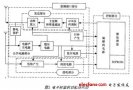
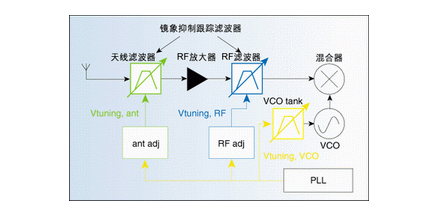
接收器必须很灵敏地侦测到小的输入讯号。一般而言，接收器的输入功率可以小到1 μV。接收器的灵敏度被它的输入电路所产生的噪声所限制。因此，噪声是设计接收器时的一个重要考虑因素。而且，具备以仿真工具来预测噪声的能力是不可或缺的。附图一是一个典型的超外差（superheterodyne）接收器。接收到的讯号先经过滤波，再以低噪声放大器（LNA）将输入讯号放大。然后利用第一个本地振荡器（LO）与此讯号混合，以使此讯号转换成中频（IF）。前端（front-end）电路的噪声效能主要取决于LNA、混合器（mixer）和LO。虽然使用传统的SPICE噪声分析，可以寻找到LNA的噪声，但对于混合器和LO而言，它却是无用的，因为在这些区块中的噪声，会被很大的LO讯号严重地影响。

小的输入讯号要求接收器必须具有极大的放大功能，通常需要120 dB这么高的增益。在这么高的增益下，任何自输出端耦合（couple）回到输入端的讯号都可能产生问题。使用超外差接收器架构的重要原因是，它可以将增益分布在数个频率里，以减少耦合的机率。这也使得第一个LO的频率与输入讯号的频率不同，可以防止大的干扰讯号“污染”到小的输入讯号。

因为不同的理由，在一些无线通讯系统中，直接转换（direct conversion）或内差（homodyne）架构可以取代超外差架构。在此架构中，射频输入讯号是在单一步骤下直接转换成基频，因此，大部份的增益都在基频中，而且LO与输入讯号的频率相同。在这种情况下，必须了解少量耦合的影响力，并且必须建立起“杂散讯号路径（stray signal path）”的详细模型，譬如：穿过基板（substrate）的耦合、封装脚位与焊线（bondwire）之间的耦合、和穿过电源线的耦合。

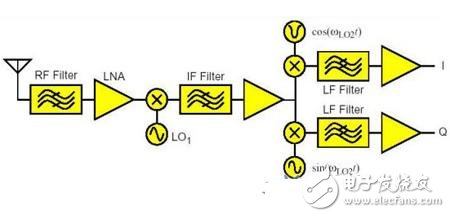
图一：典型的超外差接收器

大的干扰讯号

接收器必须对小的讯号很灵敏，即使有大的干扰讯号（阻挡物）存在时。这种情况出现在尝试接收一个微弱或远距的发射讯号，而其附近有强大的发射器在相邻频道中广播。干扰讯号可能比期待讯号大60~70 dB，且可以在接收器的输入阶段以大量覆盖的方式，或使接收器在输入阶段产生过多的噪声量，来阻断正常讯号的接收。如果接收器在输入阶段，被干扰源驱使进入非线性的区域，上述的那两个问题就会发生。为避免这些问题，接收器的前端必须是非常线性的。

因此，“线性”也是设计接收器时的一个重要考虑因素。由于接收器是窄频电路，所以非线性是以测量“交互调变失真（intermodulation distortion）”来统计的。这牵涉到利用两个频率相近，并位于中心频带内（in band）的正弦波或余弦波来驱动输入讯号，然后再测量其交互调变的乘积。大体而言，SPICE是一种耗时耗成本的仿真软件，因为它必须执行许多次的循环运算以后，才能得到所需要的频率分辨率，以了解失真的情形。

相邻频道的干扰

失真也在发射器中扮演着重要的角色。发射器在输出电路所产生的非线性，可能使传送讯号的频宽散布于相邻的频道中。这种现象称为“频谱的再成长（spectral regrowth）”。如附图二与三所示，在讯号到达发射器的功率放大器（PA）之前，其频宽被限制着；但在PA内的“交互调变失真”会导致频宽再次增加。如果频宽增加的太多，发射器将无法符合其相邻频道的功率要求。当传送数字调变讯号时，实际上，是无法用SPICE来预测频谱的再成长。因为大约有1000个数字符号（symbol）的传送作业必须被仿真，以求得代表性的频谱，并且还需要结合高频率的载波，这些将使SPICE的瞬态分析变得不切实际。

图二：数字式直接转换发射器

图三：谐波失真和交互调变失真

射频电路的特征

射频电路有几个独特的特征，是无法应用传统的电路仿真技术来仿真的。但是，在过去十年来，射频研究专家已经开发出许多种具特别功能的算法，可以用来克服这些障碍，为射频电路提供实用的仿真方法。通常这是利用射频电路的特有特征来实现的；而这些特征对传统的仿真方法而言，正是障碍之所在。底下就分别说明射频电路特有的几个特征：

* 窄频讯号

射频电路是以调变载波（modulated carrier）的形式来处理窄频讯号。调变过的载波具有周期性的高频载波讯号和低频调变讯号的双重特征，它以载波的振幅或相位或频率来调变。以典型的手机为例，它的调变频宽是10~30 KHz，“乘坐”在1~2GHz的载波上。虽然，我们常用一个正弦波或一组正弦波的简单集合，来构成调变测试讯号，但是通常，调变（输入）讯号是任意的（arbitrary）波形。

存在于调变中的最低频率与载波频率之间的比率，是相对频率分辨率的测量值，此测量值是在仿真射频电路时所必需的。一般用途的电路仿真器，譬如SPICE，是使用瞬态分析来预测电路的非线性行为。若使用瞬态分析，要在高载波频率中辨识出低频率的调变讯号，其成本是昂贵的。因为高频载波具有短的时间间隔（timestep），然而低频调变讯号需要长的时间间距。

如附图三所示，在非线性电路中传送窄频讯号时，会产生一个频谱相当稀疏的宽带讯号。一般来说，此频谱是由靠近载波附近的谐波频率丛集（cluster）而成的。如果调变是周期性或准周期性（quasiperiodic）的，则这些丛集是频率的离散形式；不然，它将是频率的连续分布。

射频仿真软件可以利用此频谱的稀疏特性，在不同状态下，得到真实的模拟效果。当频谱是离散时，“稳定状态（steady-state）法”会被使用；当频谱是连续时，瞬间分析法会被使用。

* 射频讯号路径随时间变化的线性特性

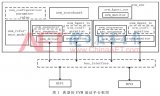
射频电路另一个重要但较少被查觉的特性是：从输入端到输出端，它们一般都会被设计成线性的电路，以避免调变或信息讯号的失真。一些射频电路，譬如混合器，是用来将讯号从一个频率转换至另一个频率。其实，它们是被一个额外的讯号LO驱动着，LO是一个大的周期性讯号，其频率是进行频率转换时所需要的。为了能得到最佳的效能，混合器被设计成可以用很强的非线性方式来响应LO。因此，混合器同时具有近似线性（至输入）和强大的非线性（至LO）特征。

产生时序（timing）或频率（clock）的电路，例如：LO，是和信息讯号无关的，因此，它可以被视为混合器的一部份，而不是混合器的外部（输入）电路，如附图四所示。这种观念上的简单改变，可使混合器具有单一输入讯号和一个近似线性、随时间变化的周期性转换函数（transfer function）。例如：有一个混波器是以一个理想的乘法器制成的，它后面跟着一个低通滤波器。乘法器是非线性的，并具有两个输入讯号。当一个LO讯号cos（ ）取得一个输入讯号之后，会产生一个转换函数值：
= LPF{ cos（ ） }
从上式清楚可知， 是随着时间变化的，并且与 成正比例的关系。如果输入讯号是： = ，那么： = LPF{ }=
上式表示一个线性周期变化的转换函数实现频率转换的功能。

图四：将LO视为混合器的一部份

通常我们会假设信息讯号很小，因此，可以将输入端到输出端之间的电路功能当成近似于线性。只要小讯号分析可以解释讯号路径的周期性变化特性，就可以进行小讯号分析。这是在接近周期发生的工作点上，进行线性仿真达成的。传统的仿真软件，譬如SPICE，支持许多小讯号分析工具，例如：交流和噪声分析，这些工具在分析放大器和滤波器时，是很有效用的。然而，它们是在接近固定的工作点上，对非线性时间不变的电路，开始进行线性仿真。因此，会产生线性时间不变的函数，但是无法代表频率转换的效果。

在一个周期变化的工作点附近，对一个非线性电路进行线性仿真，致使小讯号分析能够延伸应用到频率电路上，或者需要周期性频率讯号的电路上（此周期性的频率讯号可以让电路正常地工作），例如：混波器、交换式滤波器、取样器、和振荡器（由于振荡器是自行计时运转，所以频率讯号是振荡器的输出。信息讯号通常是不需要的讯号，譬如噪声）。若是如此，就会产生周期性变化的线性函数，而且，它的确能代表频率转换的效果。

所有传统的小讯号分析，都可以像这样被延伸应用。尤其，当噪声分析能够解释噪声折迭（noise folding）和“循环平稳噪声（cyclostationary noise）”的来源时，将可使射频电路的设计工作变得容易许多。若应用到振荡器，它也可以解释振荡器的“相位噪声（phase noise）”现象。下面简单解释一下“循环平稳”的意义：

循环平稳（cyclostationary；CS）讯号（或噪声）是非平稳讯号中的一个重要成员，或者说，它是一种特殊的非平稳讯号。其特性会随着时间呈现周期性或多周期性的变化（各周期并不相关，所以无法化约）。例如：在机械设备中，广泛存在着循环平稳讯号，特别是在滚动轴承…等复杂的旋转机械中，组件由于故障而产生周期性的脉冲力，使观测到的振动讯号明显地包含了周期性的成份。同理，在射频电路中，也会出现类似的现象，所以称呼这种讯号为“循环平稳噪声”。

* 线性的被动组件

在射频电路中，被动组件（例如：传输线、螺旋型电感、焊线封装）和基板，通常在电路特性中扮演着重要的角色。但是，由于这些组件的“天性”，常常很难将它们包含在仿真软件中。

一般而言，被动组件是线性的，可以利用分析式或S参数表，在频域以“相量（phasor）”建立模型。这可以大幅简化分布式组件（例如：传输线）模型之建立工作。大型的分布式结构，譬如：封装、螺旋型电感和基板，通常藉由一些通讯端口与电路的其它部份连接，因此，它们的行为可以轻易地用一个具有N端口的巨型模型（macromodel）来表示，此模型具有N2个转换函数。这些转换函数取代了许多个描述大系统的方程式，它们以高斯消去法来描述这些结构，仅留下与通讯端口讯号有关的方程式。在前处理阶段，就对每一个频率进行相当耗时耗成本的消去步骤。若N很小，这样得到的模型在频域仿真软件中被执行和评估，其结果是很有效率的。不过，通常这只对传输线和螺旋型电感有效，对封装和基板比较无效。

时域仿真软件可以用来对一阶常微分方程式（first-order ordinary differential equation）求解。但分布式组件（例如：传输线）是用偏微分方程式来表示的，所以，分布式组件很难使用时域仿真软件来评估。通常，我们会利用离散的数学方法将偏微分方程式转换成一组一阶常微分方程式。不过，这种方法会受限于频宽的大小。

另一种替代方案是对在频域中得到的分散组件，求出它的脉冲响应（impulse response），并使用回旋（convolution）法，求出此组件在电路中的响应。使用这种方法来评估损失性（lossy）或分散性（dispersive）的传输线模型或S参数表，其成本通常会比较高，而且容易出错。封装、基板和螺旋型电感可以使用大型的“集总网络（lumped network）”来建立模型。不过，这些系统可能会因为太过庞大，而无法有效地结合到时域仿真软件里面，因此必须采取某种消去的措施。

* 半导体模型

射频仿真软件所使用的半导体模型，必须能准确地将组件的高频和小讯号特性建立在模型里面，如此才可以准确地预测射频电路的行为。过去，双载子接面晶体管（BJT）常被应用在高频模拟电路中，它们的模型也适合射频电路。不过，从微米制程盛行开始，制造射频电路就改以标准的CMOS制程为主。但是，现有的MOS模型并不适合射频应用电路。尤其，在逻辑闸和基板中的分布式电阻并没有纳入模型中，这会影响到驱动点的阻抗和转换函数，甚至造成噪声。

此外，闪烁噪声（flicker noise）也没有纳入模型中；它是振荡器相位杂音的主要来源；对CMOS振荡器尤其重要，因为MOS组件会产生大量的闪烁噪声。

结语

EDA工具逐渐使射频电路的设计工作制式化和简单化，但是，射频工程师仍然需要了解基本的射频工程知识。这就好像现代的画家或摄影师最好仍然懂得素描的技巧一样，当遇到问题或情景时，能够从基本原理中找到灵感和答案，而不是只会操作计算机，根本就忘记了要如何“心算”。

本文不只介绍一般的射频模拟电路，还提到射频芯片的特性。因为目前国内大多数的硬件工程师和芯片设计业者，仍只重视传统的射频模拟电路，缺乏射频全芯片设计的完整认识，所以，常遇到许多技术问题而无法立即克服。这也是本文最后要强调的。