说在前面
1.写作目的
文章《萌新笔记-天线(原理篇)》介绍了天线分析的基础理论、常用工程参数以及常见天线的辐射特性分析,但是没有针对阵列天线进行深入介绍。最近在开展相控阵+载体的一体化仿真研究,其中相控阵的仿真实现需要依托Matlab-FEKO-API,会涉及到相控阵单元间距、馈电幅度/相位分布计算、波束扫描的实现等相关设计问题,籍此对阵列天线的分析和综合基础进行了系统学习。
2.内容涉及
本文的行文逻辑将从以下四个方面展开:
底层认知:将通过最通俗易懂的语言对于天线的辐射机理进行描述,帮助读者建立起对阵列天线辐射机理最直观的认识;
理论基础:分为直线阵列和平面阵列两大类,详细阐述阵列天线分析理论基础以及主要的综合方法。理论基础的学习主要基于阵列天线的学习主要依托王建的《阵列天线分析和综合讲义》、薛正辉的《阵列天线分析和综合》以及诺斯罗普-格鲁曼天线工程师布朗的《电扫阵列——MATLAB建模与仿真》三本教材展开:
学术前沿:针对一些最新的硕、博论文,进行系统学习,就阵列天线的两个主要研究方向(阵列综合算法和阵列天线工程设计)进行开展,基于前面设计的阵元幅、相分布,完成一个阵列天线的设计;
仿真实践:针对阵列天线的相关应用场景,基于仿真软件HFSS、FEKO,介绍阵列天线几种实现方法,仿真实践的学习主要基于ANSYS和Altair官网培训视频、帮助文档以及李明阳、徐兴福、谢拥军所著的HFSS培训教材展开。
底层认知
”干涉“和”衍射“是区别”波“和”粒子“的两个基本特征,电磁波作为”波“的一种,自然也具备”干涉“和”衍射“现象。其中,所谓”波的干涉“,即具有相同工作频率的两个或多个波源所产生的波在空间传输的过程中,会发生叠加的现象,从而形成”波峰“和”波谷“交替出现的现象(图片来自网络)。
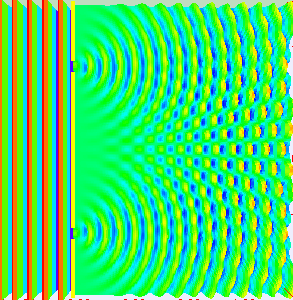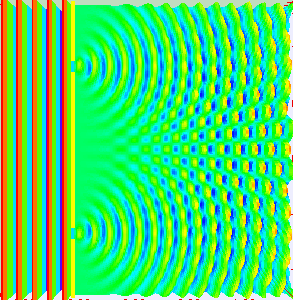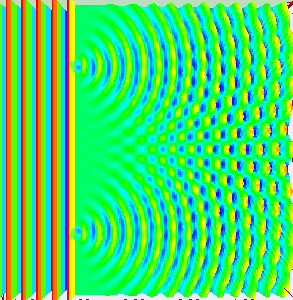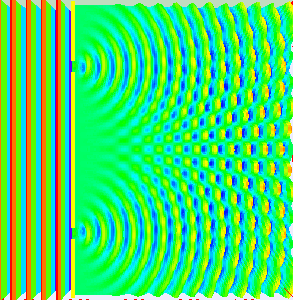
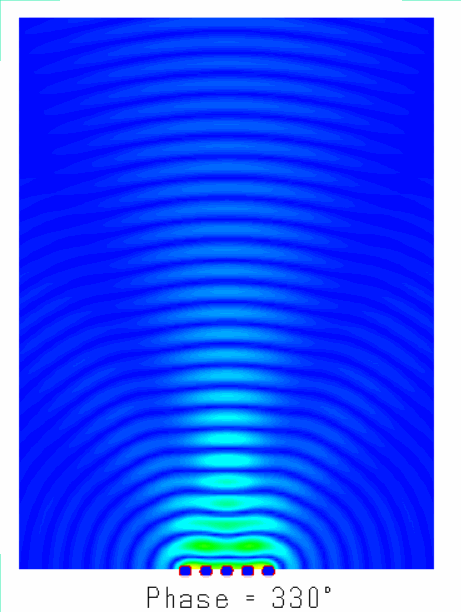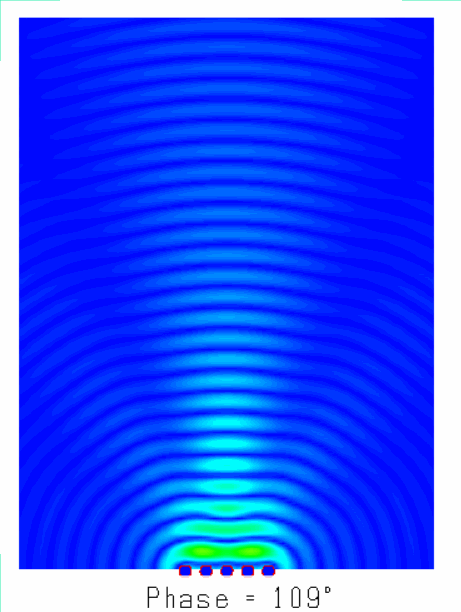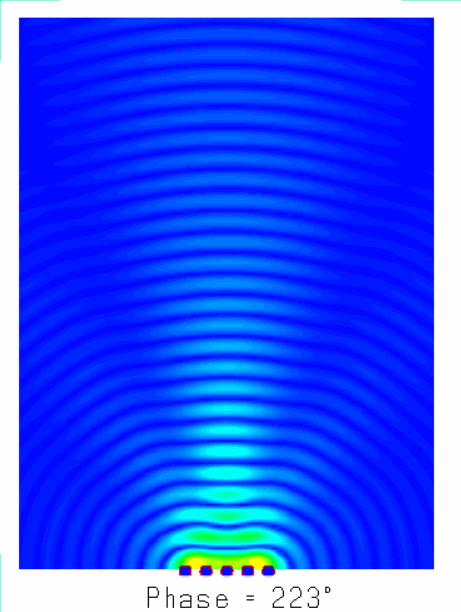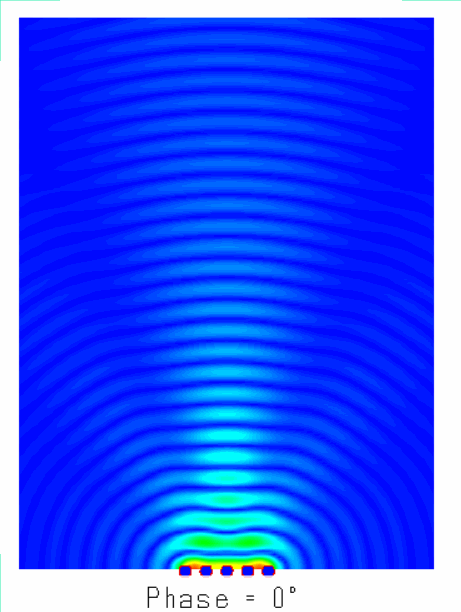
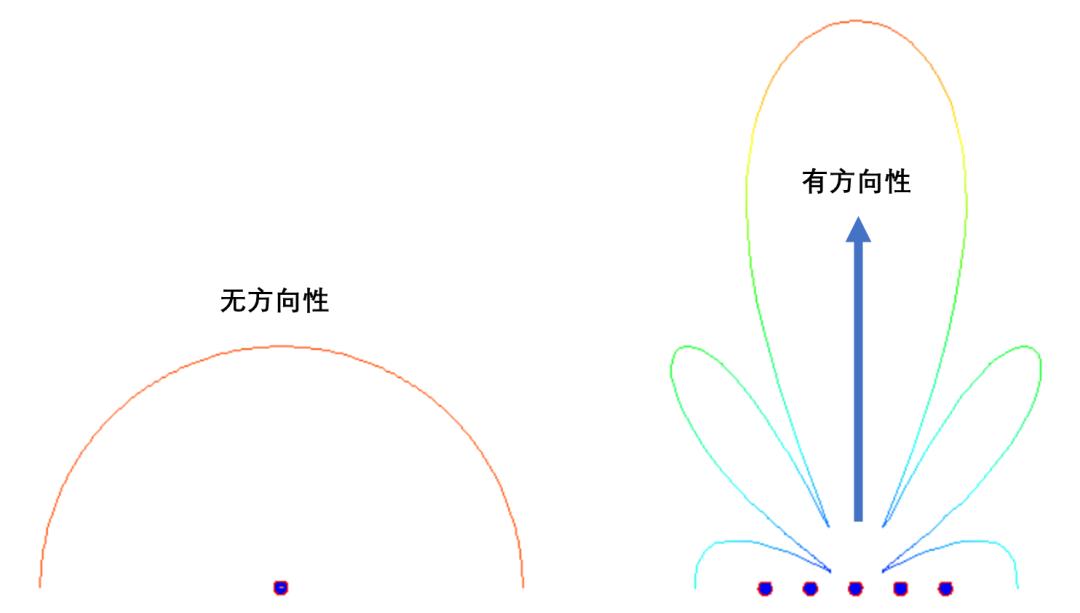
阵列天线的辐射机理就是大量天线单元辐射的电磁波产生了”干涉“现象,不同天线阵元辐射的电磁波,同相叠加时,产生波瓣,在反相相消的地方,形成零点。如图所示为含有5个单元的阵列天线的近场和远场分布图像,由由图可知:一方面电场如同波浪起伏一般由近及远的向前传播,另一方面,不同于单天线的近场分布,阵列天线的电场分布沿周向的分布并不均匀,可以发现在某些扇区较亮(场分布同相叠加),而在某些扇区则较暗(场分布反相相消),从而导致天线阵列的远场方向图表现出明显的方向性。

理论基础
1.直线阵列分析与综合
1.1 直线阵列分析
阵列天线性能主要取决于四个参数:
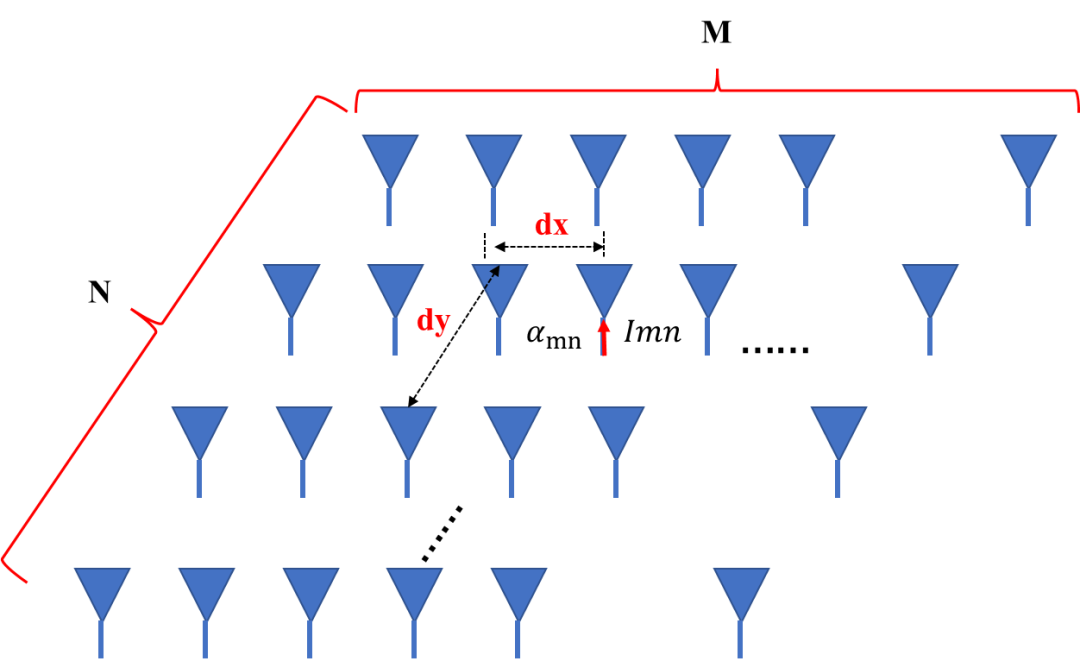
单元总数:如直线阵的N,平面阵的M*N;
单元空间分布(周期):如直线阵的d,平面阵的dx和dy;
单元激励幅度分布:如直线阵的,平面阵的 ;
单元激励相位分布:如直线阵的 ,平面阵的。
电流源的辐射场
正如《萌新笔记—天线(原理篇)》一文中所介绍的,空间中的电/磁场可经由辐射体上面的电流分布求得,一般有两种方法:1)直接法:直接利用格林函数机进行计算,2)间接法:使用“位函数”进行过渡,先通过辐射体表面电流分布建立“位函数”的表达式,再利用“位函数”计算电磁场分布。
电场分布与磁失位和电标位之间的关系为:
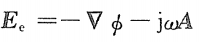
带入maxwell方程组,即可建立“A”和“”满足的波动方程:
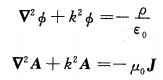
可知,中间变量满足的波动方程的形式要比“E”和“H”满足的波动方程的形式简单很多,由《电磁CAE设计师的你,有必要了解计算电磁学吗?》文章可知,该方程的解可以借助“格林函数”快速求出:
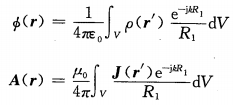
求出中间变量的空间分布后,利用“E”、“H”与中间变量的关系,即可求解出空间中电磁场的分布。远场区:,为小量,近似省略,因此有:
矢量位与“Z轴”平行,远场区电场只有“”方向分量(电场远区封闭,“r”方向分量趋于0):
则有:
其中表示源点的坐标,R表示源点与场地之间的间距:,带入电场表达式,可得:
下面以等幅激励的均匀直线阵列为例,介绍阵列天线的阵因子、波束指向、增益、波束宽度、副瓣电平等主要参数。
阵因子方向图
任意形式单元天线的远区辐射场可以统一表示为一下形式:
其中表示每个天线单元的馈电(幅度和相位),表示由于天线电流的分布导致远场分布的方向性,即单元方向图,而则是“格林函数”项,表示理想点源的远场分布形式。三部分共同框定了天线单元对远场辐射总场的贡献。
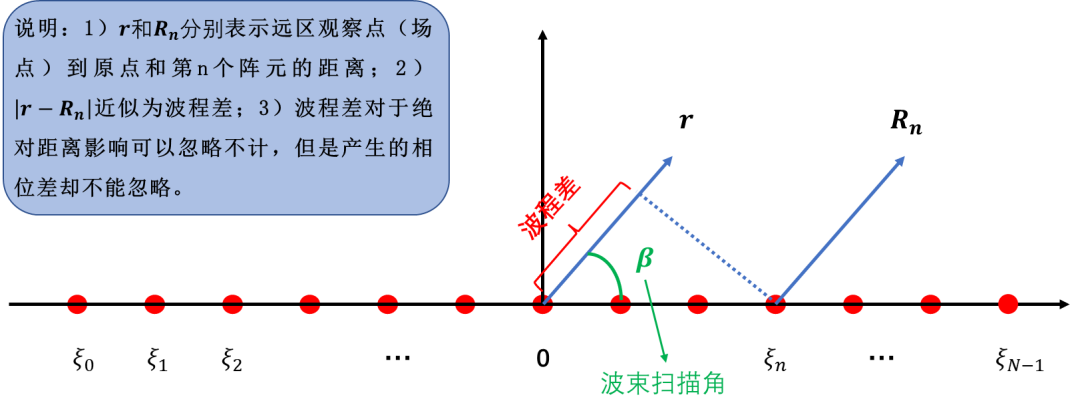
阵列的辐射总场可以简单的表示为各天线单元辐射场的叠加,即为:
其中为第n个单元源点与场点的距离:为波程差,即第n个单元源-场距离与原点-场点距离之差,带入化简可得:
天线单元的馈电部分可以表示为“复数”形式,即为:,则总场可以化简为:
其中,为阵因子,表示天线单元的组阵给远场方向图带来的二次赋形。至此,直线阵列天线的远场方向图就算完成了求解,其结构组成也非常清晰,由三部分组成:
第一项为“格林函数”项,表示理想点源在空间的场分布,其为各向同性的;
因为天线单元表面电流的连续分布,使得远场方向图被“一次赋形”,“赋形因子 ”即为单元方向图;
因为单元组阵,使得远场方向图被“二次赋形”,“赋形因子”即为阵列天线的阵因子。
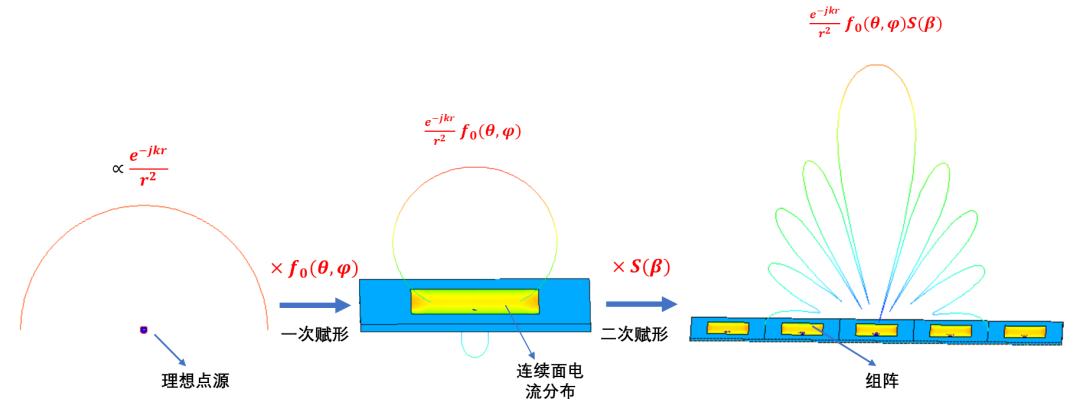
单元相位递变,因此,馈电幅度,则阵因子可简化为:
接下来将重点研究因为单元组阵而引起的“二次赋形”,即阵因子。对于均匀直线阵,,利用欧拉公式(详细推演见参考教材),阵因子可以化简为:
其中。
波束指向
当时,利用无穷小理论,取最大值,为方向图的主瓣方向,主瓣指向可以利用进行确定:
当所有单元相位一致时,即,则,波束未扫描;当各单元相位均匀递变时,则波束指向则随着的变化而进行变化,即为相控扫描,这就引出了相扫阵列的一个基本逻辑:
波程差=相位差
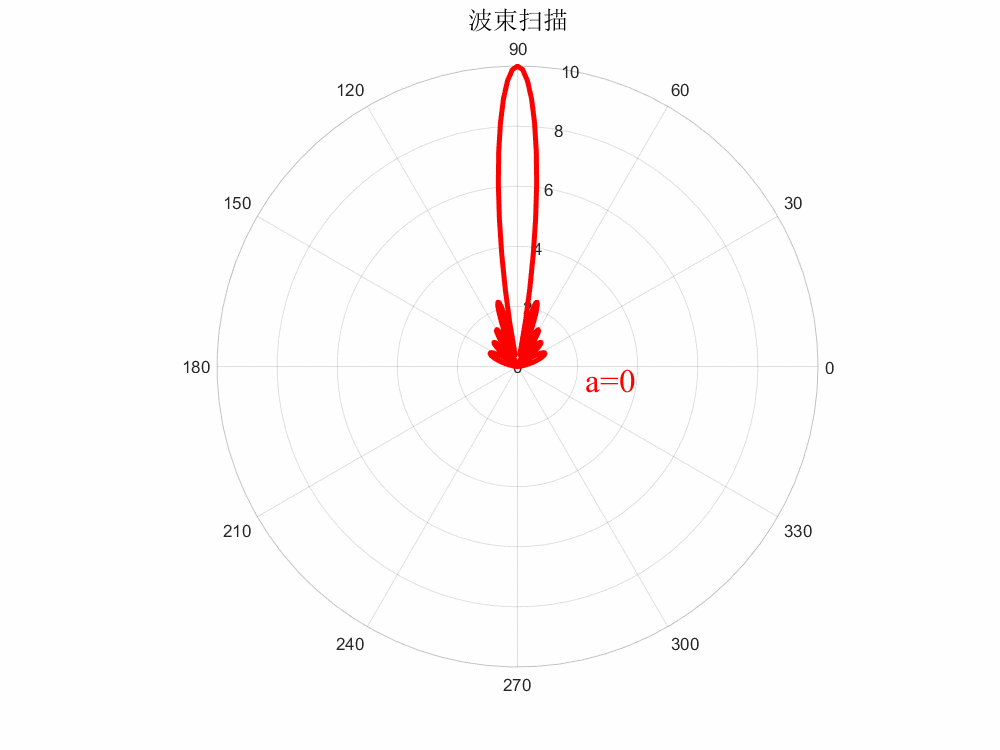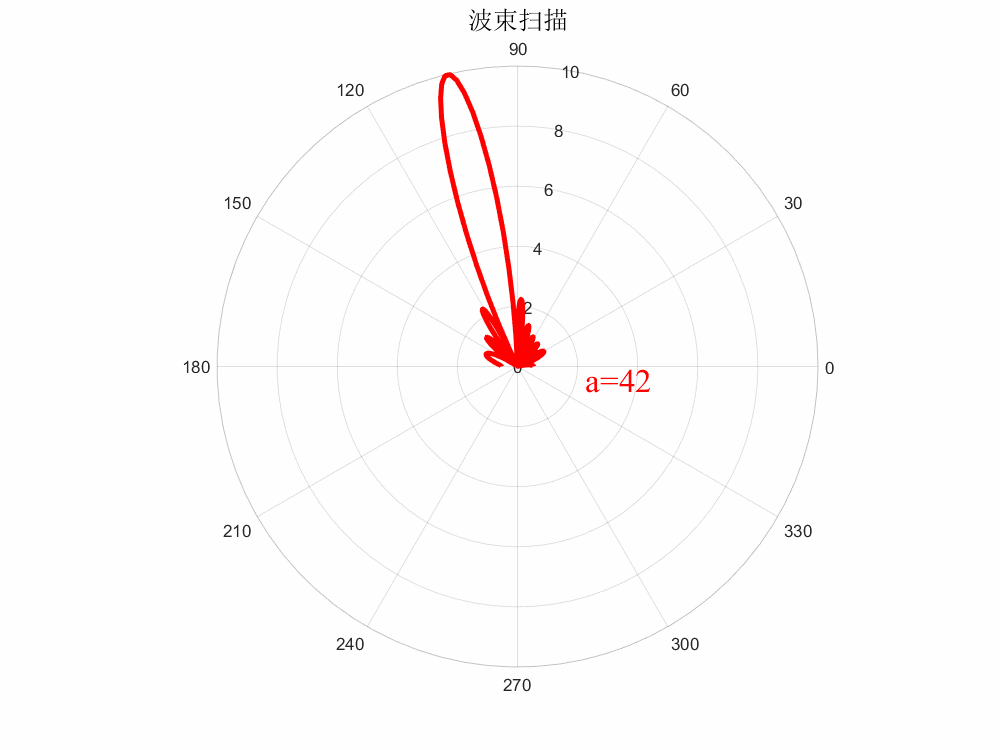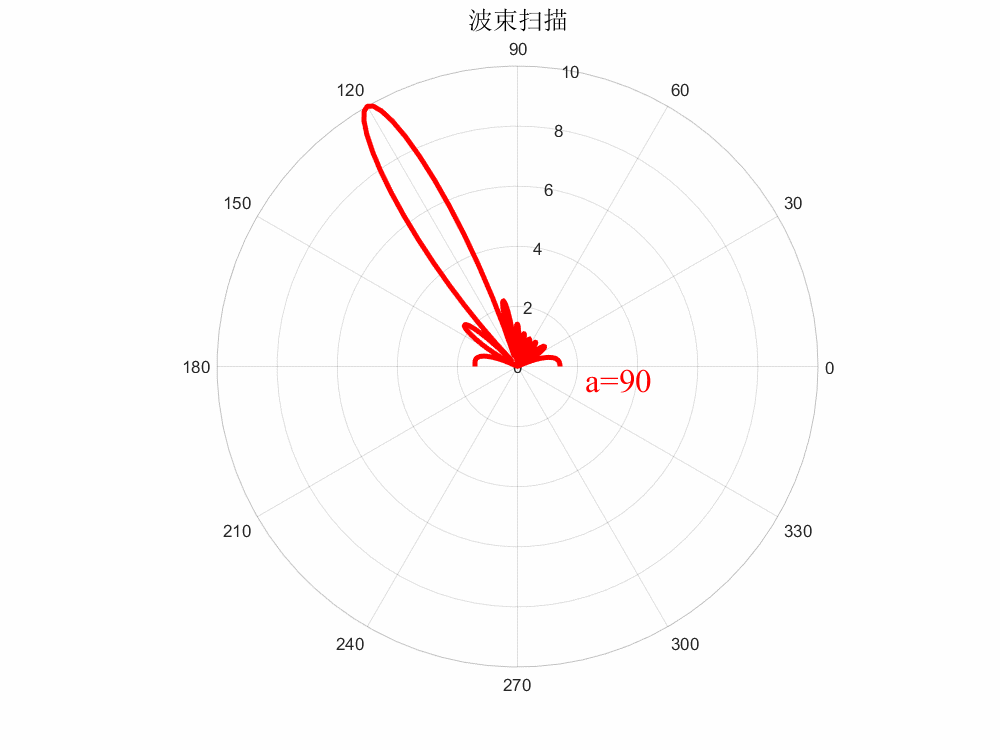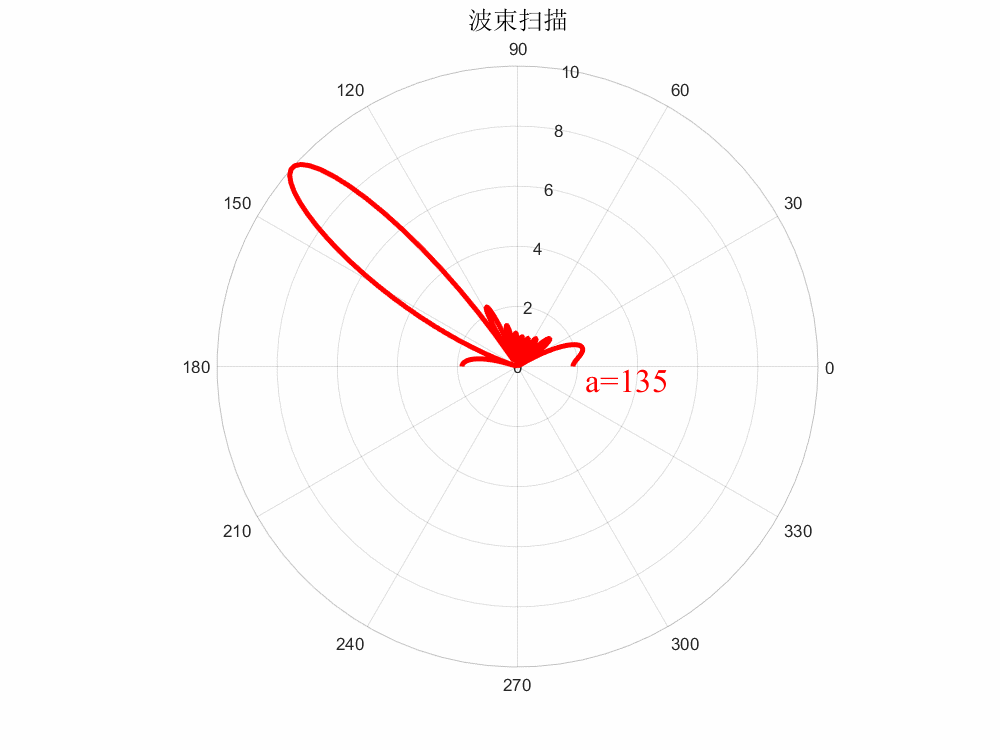
% matlab绘制动态波束扫描(保存GIF格式) clc;clear all; %%参数列表 a=0; %相位差 N=10; %阵元数目 c=3e9; %光速 freq=10e9; %工作频率 lambda=c/freq; %波长 d=0.5*lambda; %阵元间距 k=2*pi/lambda; %波矢 %% x=0180; figure(1); set(gcf,'position',[0,0,800,600],'color','w'); for i=1:47 str_title = strcat('color{red}a=',num2str(a)); y=abs((sin(N.*(k.*d.*cos(x.*pi./180)+a.*pi./180)/2))./sin((k.*d.*cos(x.*pi./180)+a.*pi./180)/2));%方向图函数 a=(i-1)*360/120; %相位差扫描范围 figure(i); set(gcf,'position',[0,0,800,600],'color','w'); p1 = polarplot(x.*pi./180,y,'r','LineWidth',3); hold on; title('波束扫描','fontsize',15); text(-0.2,2.3,str_title,'FontName','Times New Roman','FontSize',20); %%保存为gif格式 frame = getframe(gcf); im = frame2im(frame); [I,map] = rgb2ind(im,256); if i==1 imwrite(I,map,'波束扫描.gif','gif','Loopcount',Inf,'DelayTime',0.05); else imwrite(I,map,'波束扫描.gif','gif','WriteMode','append','DelayTime',0.05); end close(figure(i)); end
主瓣宽度
天线的主瓣宽度通常指方向图主瓣增益下降3dB(半功率)时所对应的波束宽度,功率下降为原来的0.5倍,则电场幅值下降为原来的0.707倍(),即有归一化阵因子:
=0.707
其中,对于侧射阵(端射状态详见教材),主瓣指向,经过化简计算,可得波束宽度:
为波束扫描角。可见:1)阵列单元数目N越大,波束越窄;2)扫描角度(相对侧射状态)越大,波束越宽,利用该公式可以在阵列设计之初,对天线阵列的波束宽度进行估计。
方向性系数D
均匀直线阵的方向性系数D定义为主瓣最大方向的功率密度与平均功率密度之比,可以由如下公式进行计算:
其中为归一化阵因子,,对进行计算,可得:
则方向性系数D为:
其中为阵列长度(口径)。
副瓣电平
副瓣电平为天线的重要技术指标,乃至于后续天线综合的主要工作就是围绕着副瓣电平SLL的优化而开展的。其定义为最大副瓣与主瓣之比,即:
对于均匀直线阵,第一副瓣即为最大副瓣,此时,其中,带入公式,可以算的:
=-13.5dB
即均匀直线阵的副瓣电平并不是特别优秀,想要获得更低的副瓣电平,还需要进一步对阵列单元的馈电幅度进行一定的设计,这就是“阵列综合”的知识了。
栅瓣抑制
由上文可知,均匀阵线阵列的阵因子为:
为周期函数(周期为,取绝对值后周期为周期为),即与主瓣等高的波瓣会每隔出现一次。
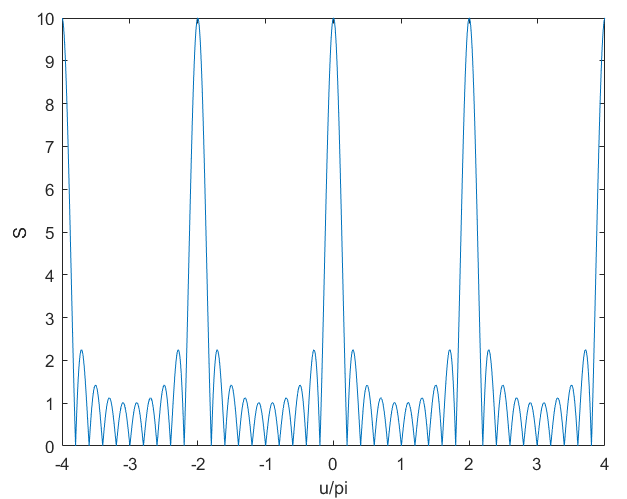
因此要抑制栅瓣的出现,就需要对u的取值范围,即,化简可得:
此即为均匀直线阵的栅瓣抑制条件。
1)对于侧射阵:,则有;
2)当波束扫描时,按扫角计算,则取,
,一般取
1.2 直线阵列综合
等幅激励直线阵的副瓣电平太高,无法满足工程上的使用要求,因此提出两种阵列综合的方法,目标是降低天线的副瓣电平。阵列综合方式:已知方向图参数(副瓣电平等),求解阵元的电流分布(幅度+相位),最主要的的是求电流的幅度分布,相位分布依据波束指向,根据“相位差=波程差”的原则进行计算,与综合方法无关。
其中之一为切比雪夫综合法,该综合法是一种等副瓣的综合方法,其特点为:
等副瓣电平;
在相同副瓣电平和相同阵列长度下主瓣最窄,在主瓣宽度一定的情况下旁瓣最低,为最佳阵列;
单元数多(N>13)时,阵列两端单元激励幅度跳变大,使馈电困难。
为了防止读者陷入浩瀚 的公式推演而迷失方向,先介绍一下“切比雪夫综合“的实现思路:1)第一步就是基于切比雪夫多项式建立一个目标方向图表达式;2)第二步就是计算N元阵的方向图表达式,并令其与目标方向图相等,从而计算出阵元幅度分布。
切比雪夫多项式
切比雪夫多项式为如下二阶微分方程的解:
令
则上式可化简为:
方程的一个解为: 同时,基于三角恒式: 可得切比雪夫多项式的递推关系式: 利用递推关系式可计算得到任意阶切比雪夫函数的“多项式”表达形式:
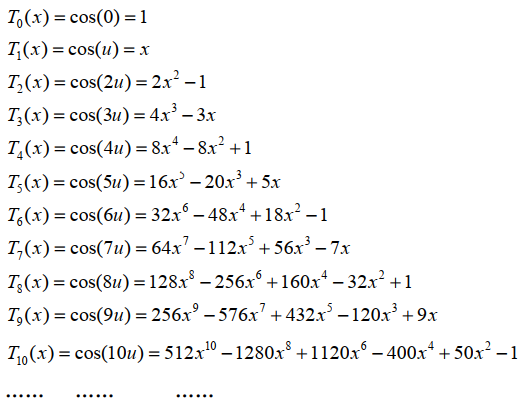
上面为的函数形式,当时,则变成双曲余弦的形式,整合下来,切比雪夫函数的“三角函数”表达形式为:
利用matlab作图可以画出任意阶切比雪夫函数曲线如下图所示,由图可知当时,切比雪夫多项式为振幅为1的振荡曲线,当时,曲线快速上升,若将作为方向图主瓣位置,将区域作为方向图的副瓣区域,则可以实现方向图的副瓣电平SLL的调节。
clc;clear all;close all; x=-1.11.1; y=zeros(1,length(x)); for m=15 for i=1:length(x) if abs(x(i))<1 y(i)=cos(m*acos(x(i))); elseif abs(x(i))>=1 y(i)=cosh(m*acosh(x(i))); end end plot(x,y); hold on; end
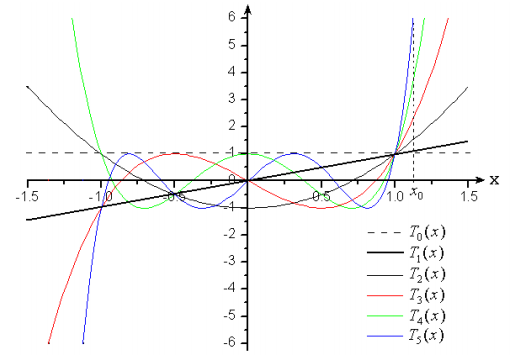
乍一看,曲线很乱,很难将其与阵因子方向图联系起来,现在我们尝试通过一系列变换建立其与方向图的联系(取n=8,函数曲线取坐标系的正半边进行考察),变换过程如下:
取的切比雪夫多项式进行研究,由图可知时,曲线在内振荡,的位置决定了的高度,曲线如图1所示;
令,将曲线定义域收缩至[0,1];
对表达式取绝对值,即忽略电场方向带来的“正负”,统一考察电场幅值大小;
令,会发现原本的函数曲线竟然神奇变成了我们熟悉的方向图。由图可知:1)该方向图所有副瓣均相等(等副瓣);2)副瓣电平始终为1,主瓣电平为,主副瓣比SLL的大小取决于最初选择的的大小,即主副瓣比可调。
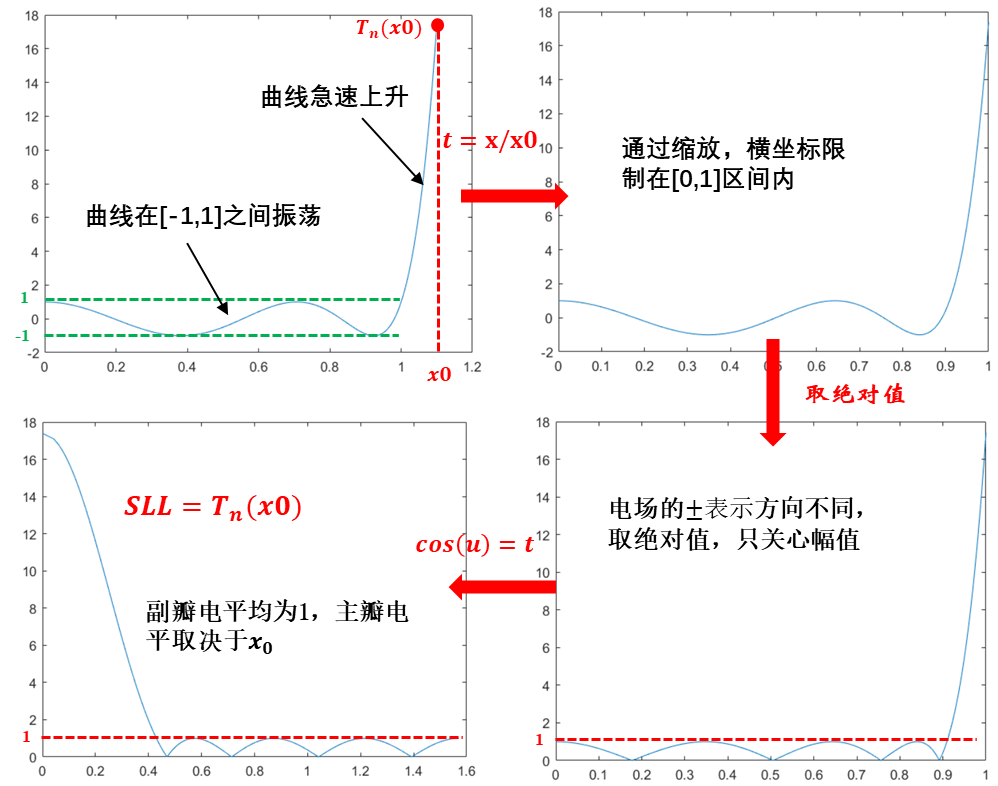
切比雪夫综合
由上面可知,经由切比雪夫多项式,通过适当的变换,就可以得到主副瓣比可调的等副瓣方向图,下面就需要建立目标阵因子和切比雪夫函数的关系,以期实现相同的方向图分布特性。非等幅的直线阵列的的阵因子为:
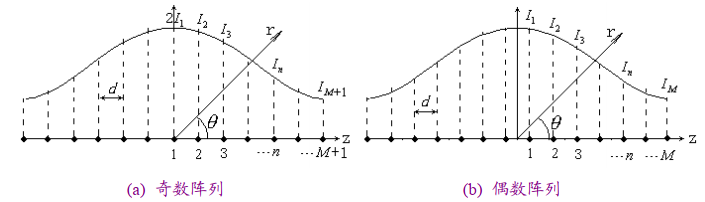
设馈电幅度为对称分布,按照阵元数目的奇偶,依据欧拉公式,对称位置两两相消,阵因子可以化简为:
当均取1时(即为等幅),计算可得其SLL明显小于切比雪夫阵:
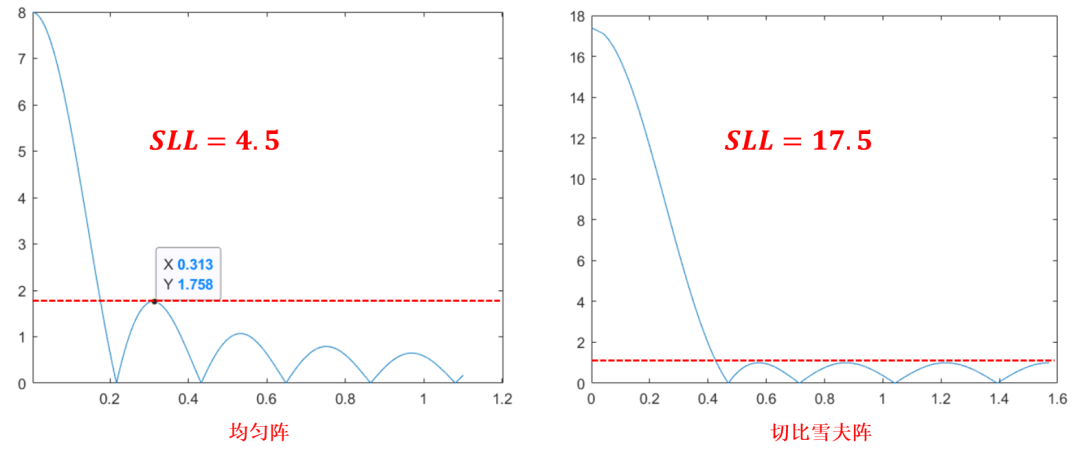
如果令:
我们就会发现阵因子中的每一项都是一个切比雪夫多项式,其中:
因此阵因子表达式即为一系列切比雪夫多项式的和:
总结下来,切比雪夫阵的设计思路为:如果希望待优化阵因子变成理想方向图,那么就需要令其等价的切比雪夫多项式之和与相应最高阶切比雪夫多项函数相等,从而求出阵列馈电幅度分布{......}。同时,通过的调节,即可实现方向图副瓣电频SLL的调节。
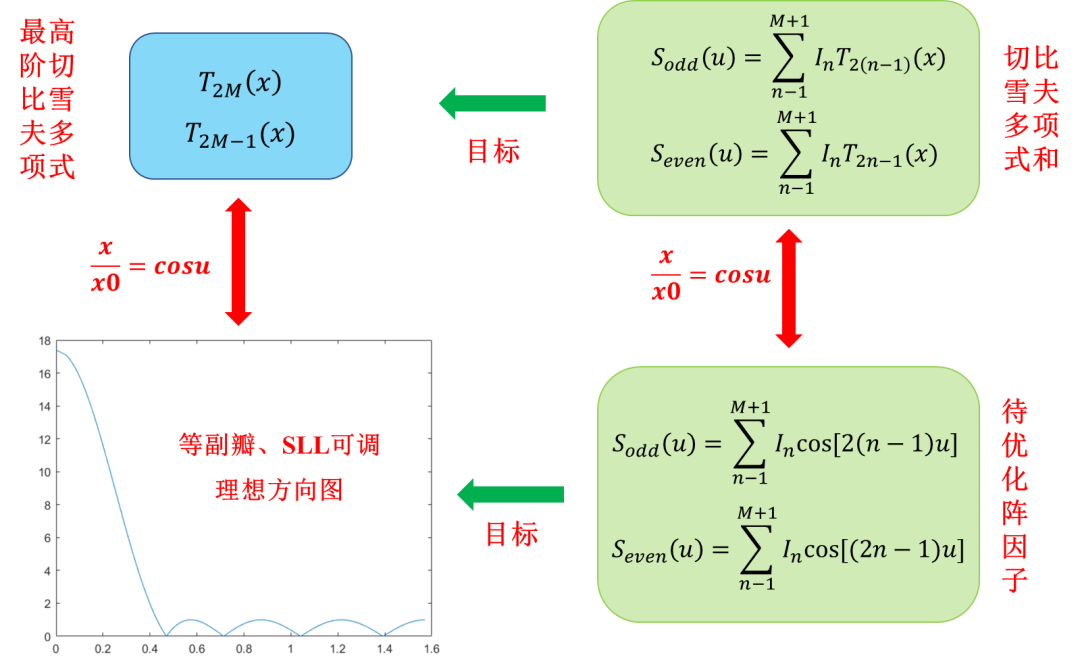
实际工程中,无需手动计算出切比雪夫综合的阵元分布,利用MATLAB自带的函数即可轻松完成计算。
N=16;%阵元数目 SLL=20;%副瓣电平 w = chebwin(N,SLL);%输出阵元幅度分布 wvtool(w);%查看阵元幅度分布及方向图预览
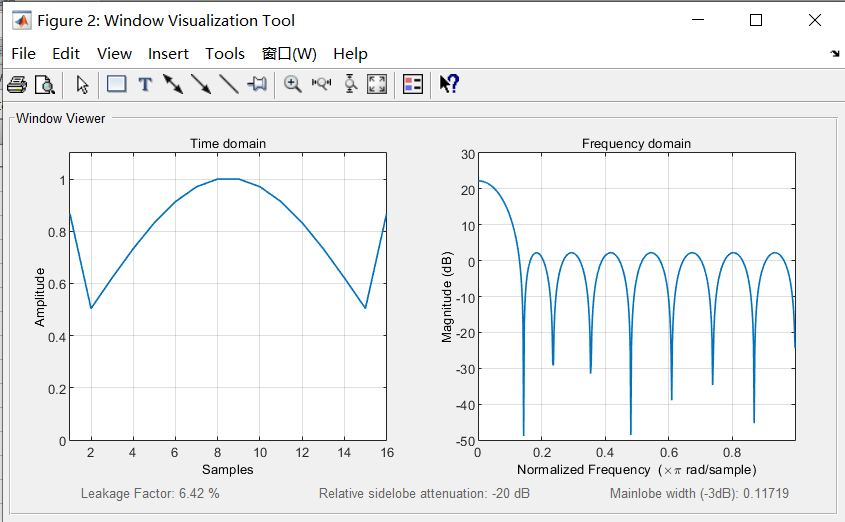
泰勒综合法
当阵列单元数目较多(),切比雪夫阵列两端单元的激励幅度将发生跳变,即最末单元比其相邻单元的激励幅度大许多,不利于馈电并对方向图副瓣电平影响很大,此时需要引入泰勒综合法。
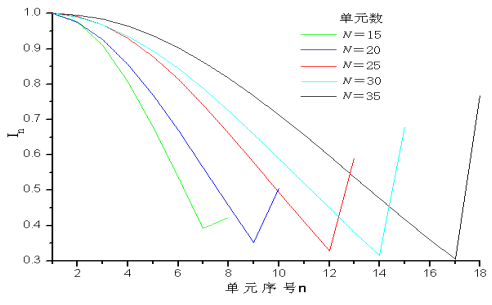
采用泰勒综合方法设计的泰勒阵列,其方向图只是靠近主瓣某个区域内的副瓣电平接近相等,随后单调减小,有利于提高天线的方向性,且激励的幅度分布的变化在阵列两端是单调减小的,不会出现两端单元激励幅度跳变的情况。
与”切比雪夫综合“类似,”泰勒综合“的思路也大致分为两步:1)依据切比雪夫多项式,结合理想线源函数,通过变换,构建目标方向图(泰勒函数);2)计算连续线源的方向图表达式,并令其等于目标方向图,从而计算出”连续线源“的分布,在对其离散,即得到N元阵列的幅度分布。
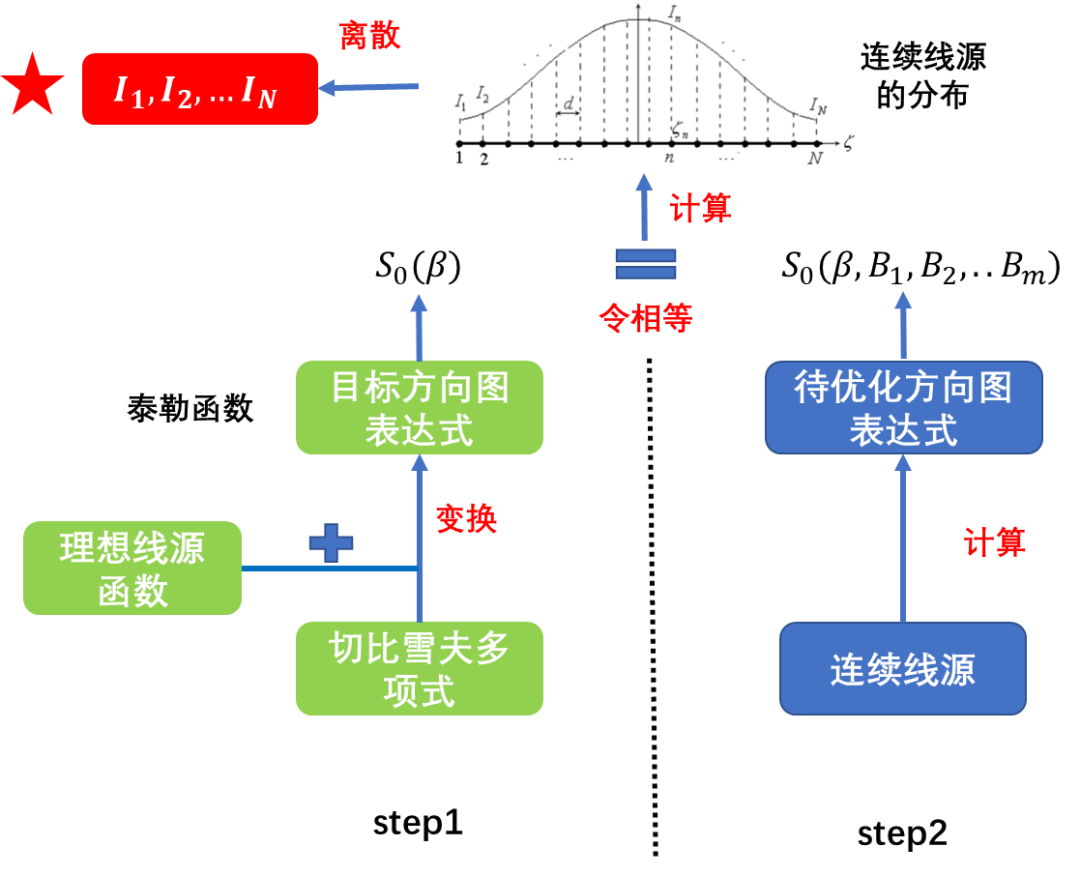
泰勒综合的参考函数起源于切比雪夫函数,令,即有:
利用MATLAB绘制其曲线如图所示,其与阵因子方向图十分相似:
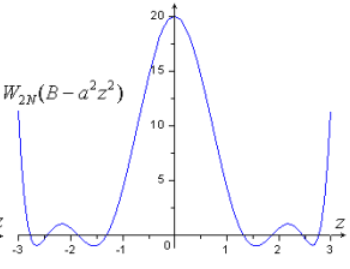
当变量N趋于时,参考函数就转化为理想线源的空间阵因子:
其方向图形式为:
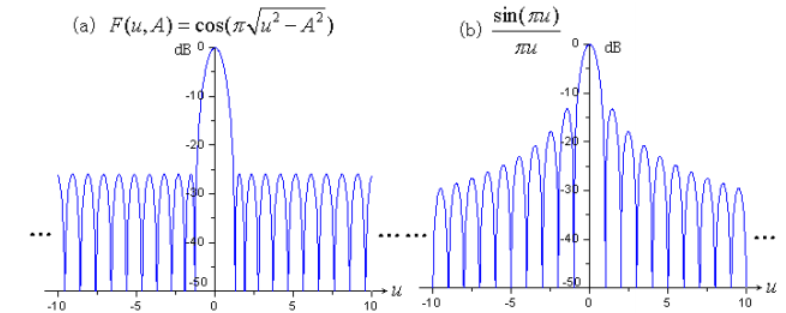
为等副瓣形式,通过引入基本函数波瓣展宽因子,改造基本函数,构建泰勒方向图函数:
该方向图函数的含义是:把基本函数前个零点用于改造的理想空间因子的零点取代,而第个以后的零点保持为基本函数的零点。
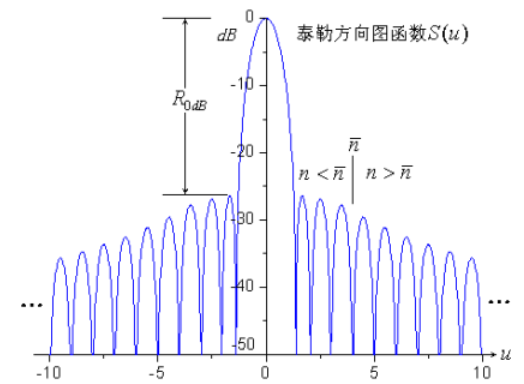
所构造的泰勒方向图函数既保持了理想空间因子可调副瓣电平和前个副瓣近似相等的性质,又在远副瓣(第个及以后)保持了基本函数的副瓣峰值以衰减的性质。总结下来,泰勒函数的构造过程如下图所示:
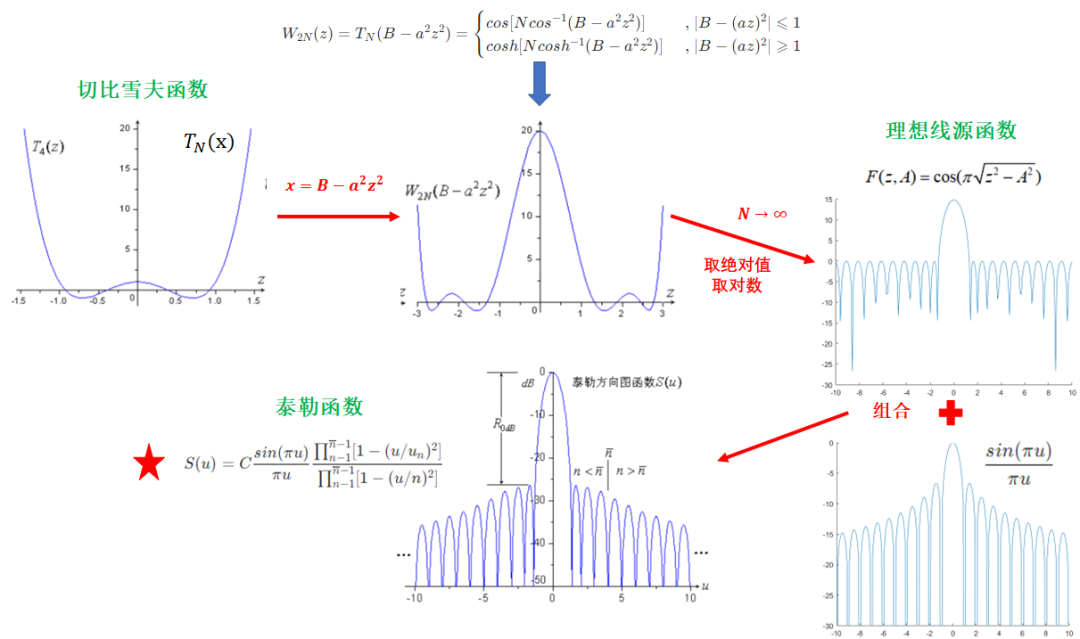
第一步,我们已经构造了一个完美的方向图函数,其有着可调的副瓣电平以及递减的旁瓣,现在所要做的就是朝着这个完美的方向图函数努力前进,让待优化阵因子与其相等,从而求出阵元幅度分布即可。
连续线源的方向图
从连续线源的方向图分布聊起,假设其电流分布为:
其中展开系数为未知项,该电流分布所对应的空间阵因子的表达式为:
这就是待优化阵因子的表达式,令其等于泰勒方向图阵因子,即可求解出展开系数从而完成了连续线源电流分布的综合。
上式即为综合得到的连续线源的电流分布。对于直线阵列的各单元的馈电分布,只需要对连续电流进行抽样离散即可。
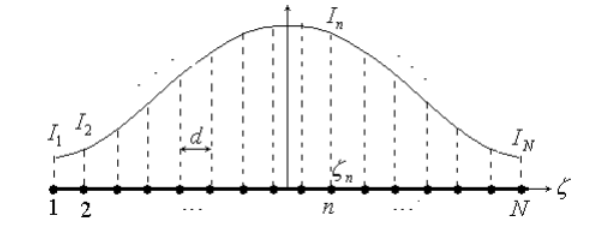
即为每个阵元的馈电幅度,其中,,
实际设计过程中,以上的综合过程无需设计师手动计算,MATLAB中内置Taylor函数,可以按照阵元数目、主副瓣比SLL和值,直接综合出相应的馈电分布。
N=64;%阵元数目 n=4;%远副瓣位置 SLL=-35;%副瓣电平 w = taylorwin(N,n,SLL); %输出阵元幅度分布 wvtool(w);%查看阵元幅度分布及方向图预览
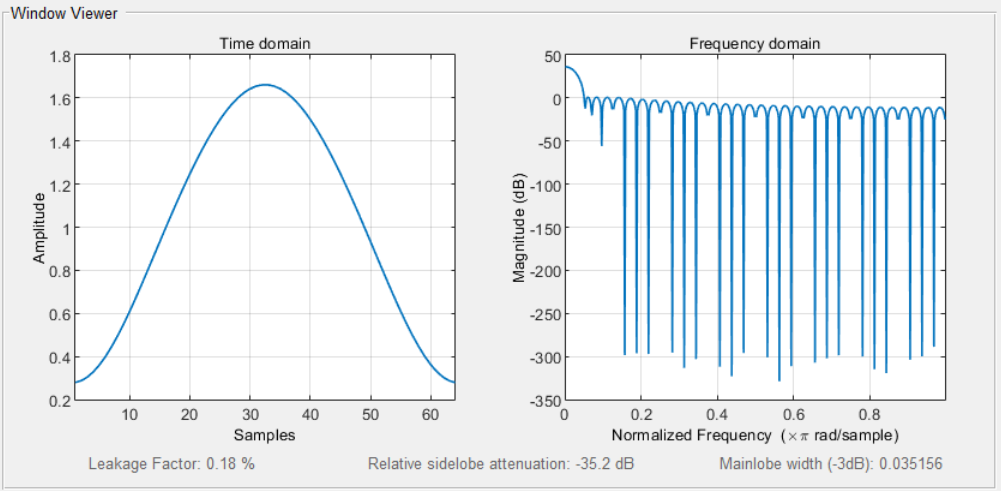
泰勒综合设计准则
依据主副瓣比选择合适的,的含义是泰勒方向图的前个副瓣近似相等,其应该根据主副瓣比来选择,一般可取,其中,为主副瓣比。
泰勒综合的单元数目不能太少,否则按主副瓣电平比的阵列方向图副瓣电平,不能达到设计目的。
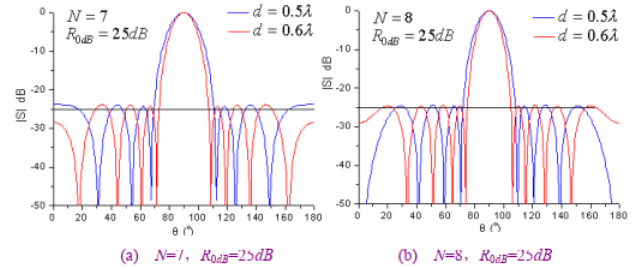
在阵列天线设计中,各单元的激励分布都是理想分布。然而实际加工出来的馈电网络总是存在误差,加之单元间的互耦误差等,阵列天线的副瓣电平实测值会有所恶化,因此副瓣电平设计值需留有余量,一般取7~10dB。
2.平面阵列分析与综合
2.1 平面阵列分析
基于直线阵列的基本原理,依托可分离原理,重点介绍“矩形栅格”形式的平面阵列。
阵因子方向图
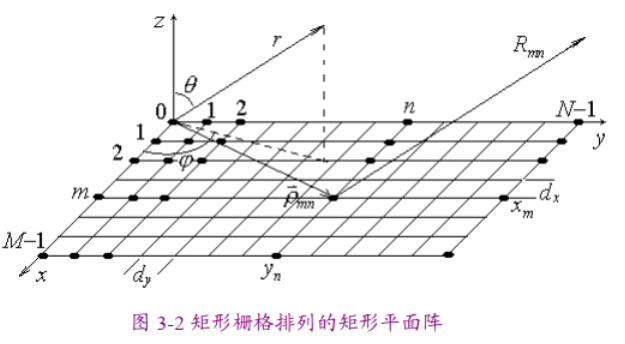
直线阵中方向图表达通式也可以被应用于平面阵列,任意形式单元天线的远区辐射场可以统一表示为一下形式:
其中表示每个天线单元的馈电(幅度和相位),表示由于天线电流的分布导致远场分布的方向性,即单元方向图,而则是“格林函数”项,表示理想点源的远场分布形式。三部分共同框定了天线单元对远场辐射总场的贡献。
其中:
则第mn个单元的远区辐射场为:
整个平面阵的远区辐射场为:
如果平面阵按列分布为;按行的分布为,则总的馈电幅相为:
为可分离型。可分离型阵列的阵因子也是可分离型的,阵因子为:
其中:
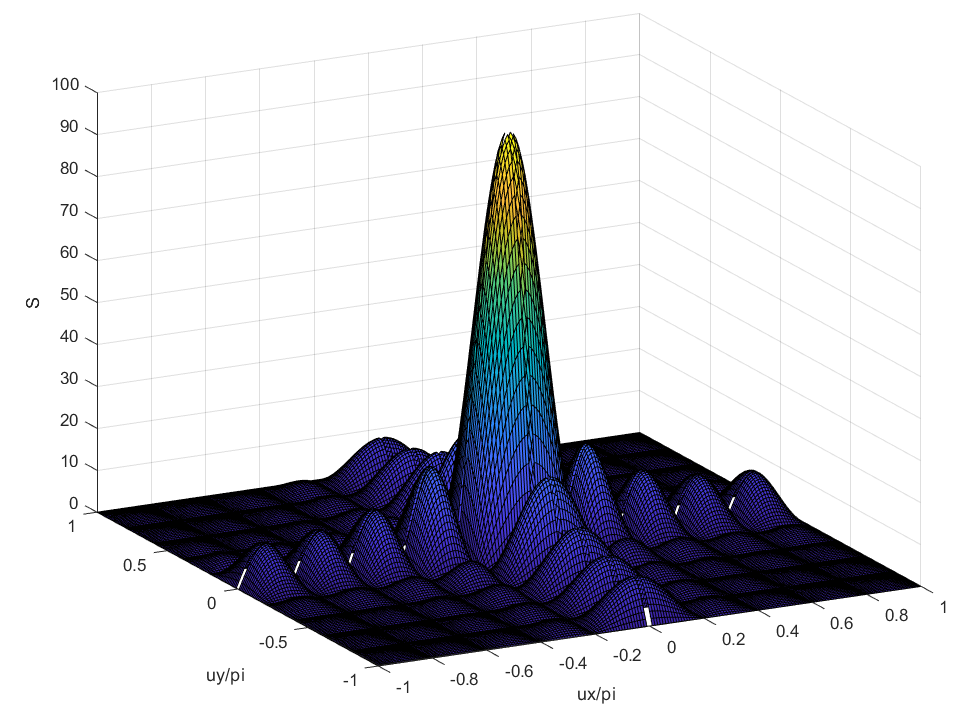
可知,矩形栅格的矩形平面阵列,如果其馈电分布是可分离,则该平面阵列的阵因子方向图就是沿x和y方向排列的直线阵列阵因子方向图的乘积,者也是方向图相乘原理的一种体现。同理,参照均匀直线阵,对于等幅分布的均匀平面阵,其方向图阵因子可以利用欧拉公式简化为:
即为均匀直线阵因子的乘积。
平面波束指向
波束扫描的核心就是:馈电相位差等于波程差
1)当时,出现最大值,此时,为波束指向,得:
同理,当时,出现最大值,得:
联立可以解的波束指向 ,相反得,可以按照期望波束指向可以求得馈电相位差。
波束宽度
经线所在平面内的半功率波瓣宽度
当(最大指向在xz平面内):
当(最大指向在xz平面内):
纬线切线所在平面的半功率波瓣宽度
当(最大指向在xz平面内):
当(最大指向在xz平面内):
即波束沿俯仰向进行扫描时,经向所在平面的波瓣宽度会逐渐展宽,而纬线切线所在平面额波瓣宽度不变。
方向性系数D
方向性系数的定义为最大增益与平均增益之比,即:
此处假设阵列数目非常多,单元方向图近似单元阵因子。
对于均匀直线阵:
2.2 平面阵列综合
切比雪夫综合法
矩形栅格矩形边界的切比雪夫平面阵有两种形式,一种是可分离型分布的切比雪夫平面阵;另一种是不可分离分布的切比雪夫平面阵。 此处介绍简单且更为常用的可分离型切比雪夫平面,其设计较为简单,即沿两个主平面方向图指标(主瓣宽度、副瓣电平),分别设计沿x轴和y轴两个方向排列的直线阵即可。
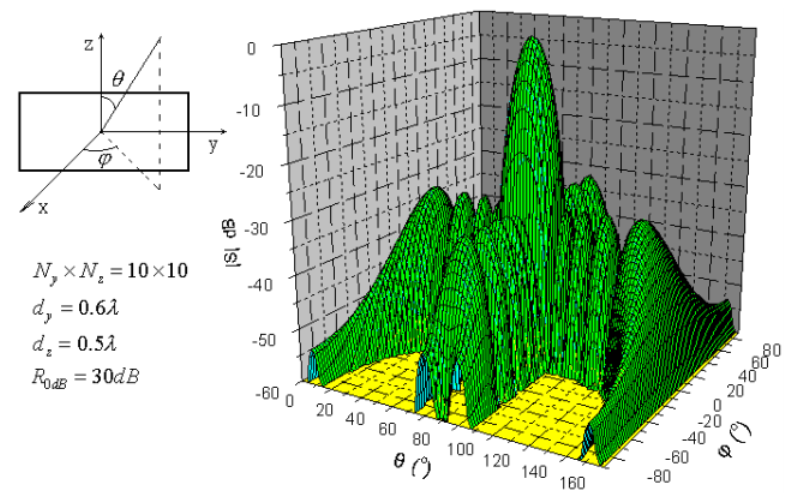
平面各阵元的馈电幅度可以通过直线阵列直接相乘得到。
clc;clear all; [x,y]=meshgrid(-7.57.5,-7.57.5); Nx=16;%x方向阵元数目 Ny=16;%y方向阵元数目 SLL=20;%副瓣电平 wx = chebwin(Nx,SLL);%输出x方向阵元幅度分布 wy=chebwin(Nx,SLL);%输出y方向阵元幅度分布 Wxy=wx.*wy'; %直线阵列的馈电幅度分布相乘得到平面阵 surf(x,y,Wxy); %阵元馈电幅度分布
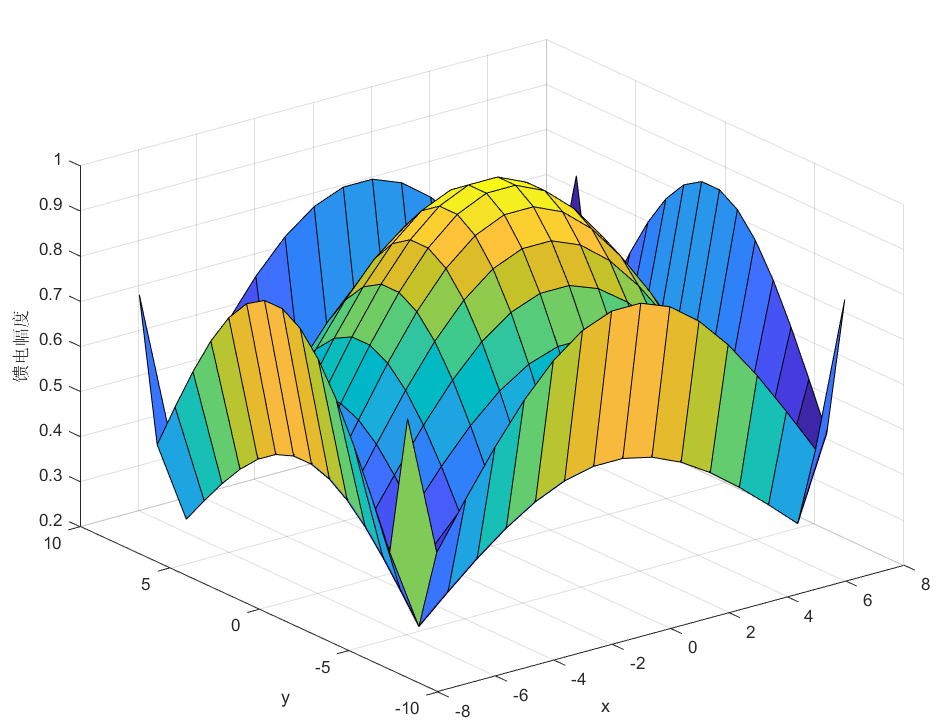
泰勒综合法
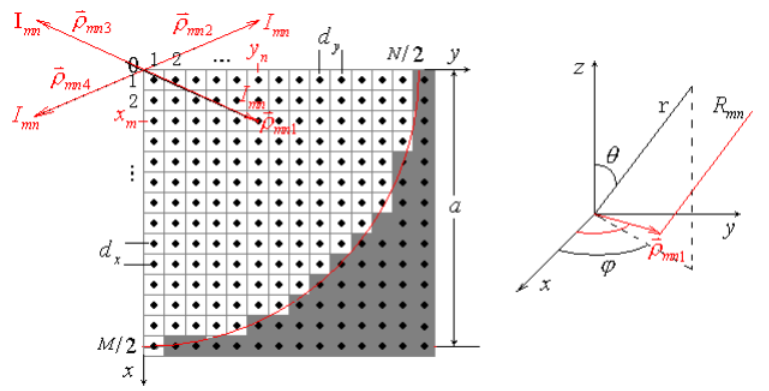
阵因子
其中:
类比于泰勒分布的“直线阵列”,圆口径泰勒分布的“目标空间阵因子”为:同样的,使用连续面源分布去拟合:计算出待定系数,即可得到圆口径泰勒面源分布,再经过离散就是圆口径泰勒阵列分布。虽然理论上,圆口径泰勒分布为不可分离型,但是在实际工程中,通常也是使用线阵泰勒分布相乘得到面阵的方式来设计泰勒分布阵列天线。
clc;clear all; [x,y]=meshgrid(-7.57.5,-7.57.5); Nx=16;%x方向阵元数目 Ny=16;%y方向阵元数目 SLL=20;%副瓣电平 wx=taylorwin(Nx,SLL);%输出x方向阵元幅度分布 wy=taylorwin(Nx,SLL);%输出y方向阵元幅度分布 Wxy=wx.*wy'; surf(x,y,Wxy);
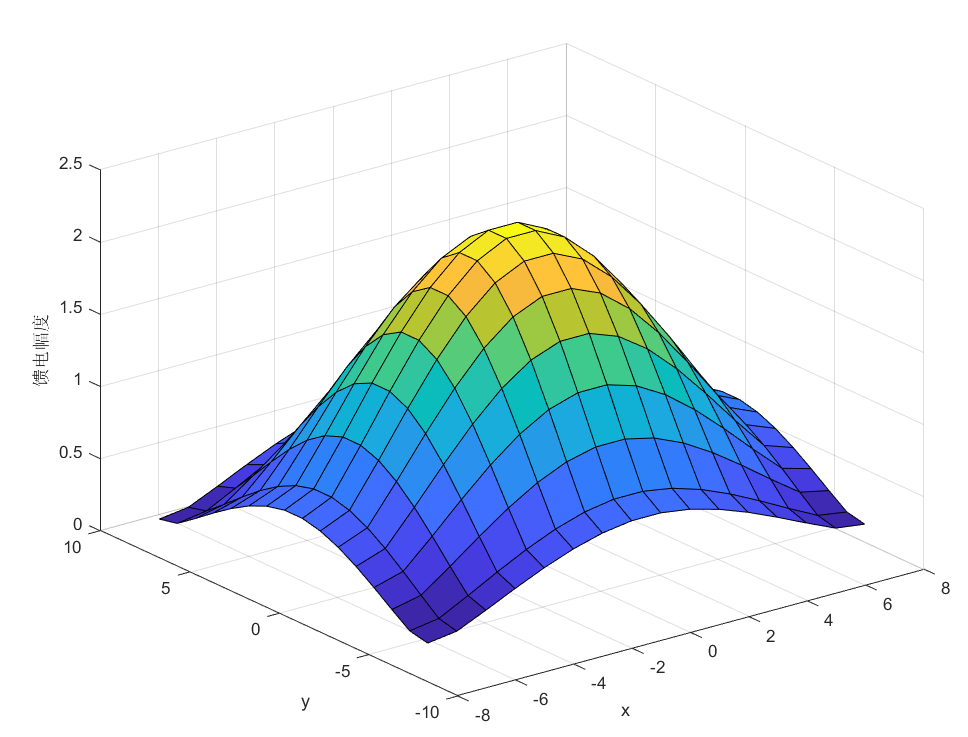
3. 单脉冲体制
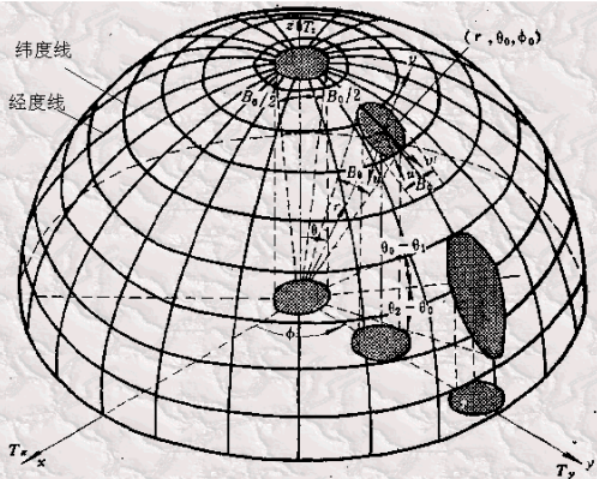
阵列天线的方向图中的和波束和差波束被广泛关注,其背景即为雷达搜索中的”单脉冲体制“。通过窄波束扫描获得目标的位置和距离信息是现代雷达的主要功能,其中“单脉冲技术”为应用最普遍的技术体制。(图片来自网络)

单脉冲雷达天线要求产生一个主瓣的和波束以及具有两个(或四个)主瓣的差波束。差波束的两个峰值之间的最小值称为“零值”。和波束的作用是探测目标的距离(r)和进行距离跟踪;差波束的作用是探测目标的方位角和俯仰角信息(,)和进行角跟踪。
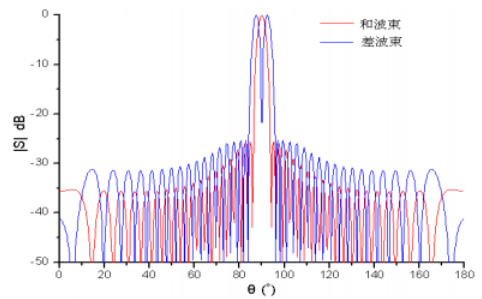
一个目标的距离信息 r 和角信息, 已知, 则目标的空间位置就确定了。如果目标正好在和波束最大值方向, 则差波束接收到的信号很弱(为零值);当目标移动时, 则差波束接收到的信号由弱变强, 则可利用差信号来驱动伺服机构, 使天线在俯仰或方位上转动,始终使差波束的零值方向对准目标,从而实现跟踪 ,同时利用和波束接收到的回波信号时间差确定目标距离。
结语
本文为”阵列天线的分析和综合基础“的理论篇,分为直线阵列和平面阵列两大类进行展开,介绍了”分析“和”综合“两部分,其中”分析“为依据阵列天线确定的幅、相分布来计算其辐射特性;”综合“则根据总体提供的方向图要求(主瓣增益、副瓣电平等参数)来反向确定天线的幅、相分布。全文在于解决”阵列天线设计“的前两步:1)由浅入深的理解阵列天线的辐射机理;2)按照阵列天线设计指标,完成阵列天线单元数目、幅相分布的计算。下一篇为”实践篇“,将在理论篇确定的阵列结构、幅相分布的基础上,介绍”阵列天线设计“的工程实现以及相关使用相关仿真软件进行”阵列天线设计“的方法。
编辑:黄飞
 电子发烧友App
电子发烧友App
























评论