射频脉冲信号典型的六个知识点总结

Test Card

脉冲信号是雷达系统最基础、最常见的信号形式，从业人员应该对这类信号有着更加深入的理解和认识。本文针对射频脉冲信号总结了比较典型的六个知识点，希望对大家有所帮助。

包络谱与线状谱

首先聊聊脉冲信号的频谱，对于接收机或频谱仪而言，当所设置的分辨率带宽RBW不同时，所“看到”的频谱也是不同的。但就信号本身而言，周期脉冲信号的频谱确实是离散的一根根谱线，如图1实线所示。

离散谱线的特点：相邻两根谱线之间的频间距为脉冲周期的倒数；以中心载波为轴，左右谱线相互对称；每一个位置的频谱线的强度都遵循Sa(x)函数分布；存在零点，距离载波最近的零点称为第一零点，与载波的频间距为脉宽的倒数。

值得一提的是，上述特点是基于理想脉冲而言的，实际测试时，由于偏离了理想脉冲，故测得的数值也会有些许的差异。

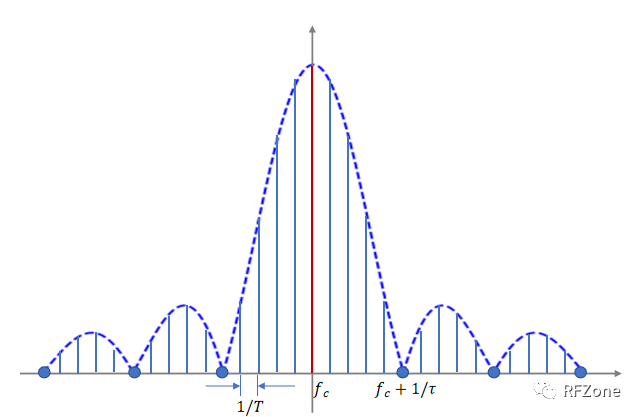
图1. 射频脉冲信号频谱示意图

虽然周期信号的频谱是离散的，但是当接收机或频谱仪的RBW设置得比较大时，将得到另一种频谱显示——包络谱，类似于图1虚线所示，将不再显示离散的谱线。这种结果并不是错误的，而是一种正常的频谱显示，这是因为RBW太大而无法分辨出相邻的离线谱线，相当于RBW内包含多根谱线，从而得到包络谱。

第一零点带宽

理想周期脉冲信号的频谱服从Sa(x)分布，Sa(x)函数有无数个旁瓣和零点，观察图1所示的频谱示意图，零点的位置很有特点，只有关于载波对称的两个零点频间距较宽，其余所有的相邻零点频间距都是恒定的，根据下面的理论计算，这个频间距为脉宽的倒数，而载波左右两个零点的频间距为2倍的脉宽的倒数。

从射频脉冲的整个频谱看，载波左右两侧第一个零点之间的频间距即为第一零点带宽。

下面采用简单的推导，对上述结论加以验证。

Sa(x) = sinx/x

当x=+/-nπ (n为非零整数)时，Sa(x)=0。

根据周期脉冲信号的傅里叶级数展开，此处的x实际对应ωτ/2，其中ω为脉冲信号的角频率，τ为脉宽。

经过推导，零点的位置为

ω = 2nπ/τ (n为非零整数)

可见，脉宽决定了脉冲频谱的第一零点带宽，射频脉冲频谱的大部分功率都集中在这个带宽内。周期一定时，脉宽越窄则第一零点带宽越大，带宽内的各个谱线的强度差异越小，整个频谱看起来“矮胖”；脉宽越宽则第一零点带宽越小，带宽内的各个谱线的强度差异越大，整个频谱看起来“高瘦”。

实测时，您可能会发现零点处的幅度并不为0，这是因为实际的脉冲并不是理想的矩形脉冲，而以上公式推导都是基于理想脉冲信号这一前提的。

峰值与平均功率

峰值功率肯定是指脉内峰值功率，实际射频脉冲的脉宽部分的幅度并不是平坦的，会有过冲(overshoot)、顶降(droop)以及纹波(ripple)，势必会存在一个幅度峰值，这就是峰值功率。峰值功率需要使用宽带功率探头或者宽带信号分析仪进行测试，前者采用二极管包络检波+高速ADC实现脉冲包络的测试，后者采用宽带采集+IQ数据后处理的方式进行测试，二者均可以实现测试功能，但功率探头可以保证更准确的功率测试。

图2. 射频脉冲信号的功率定义示意图

平均功率有两种定义，可指脉内的平均功率，也可指整个周期内的平均功率，即总平均功率，如图2所示。如前所述，脉内往往存在过冲、顶降和纹波，对脉内幅度进行统计，必然存在一个平均值，这就是脉内平均功率。测试方法与峰值功率类似，不再赘述。

总平均功率要比脉内平均功率低，尤其是占空比较小时，这种差异更加明显。如何测试总平均功率呢？其中一个方法就是根据已测得的脉内平均功率，再结合占空比即可计算出总平均功率。

还有一个大家所熟知的方法——积分带宽法，无论频谱显示为包络谱还是线状谱，使用积分带宽法均可以测出总平均功率，为了保证测试精度，积分带宽要设置得足够大，尽量包住更多的旁瓣。

脉冲退敏效应

简单讲，当显示射频脉冲信号的线状谱时，中心载波的幅度要比脉内平均功率低，具体低多少，取决于占空比。

脉内平均功率与中心载波功率的关系为

Pc = PAVG + 20lg(τ/T)

通常将 20lg(τ/T) 称为脉冲退敏因子。

需要提醒的是，线状谱时的载波功率并不是总平均功率，验证如下：

从能量守恒的角度讲，脉内平均功率与总平均功率的关系为

PAVG,T = PAVG + 10lg(τ/T)

很显然，总平均功率并不等于线状谱时的载波功率！

时间/幅度/频率/相位参数

射频脉冲信号的参数包括四大类：时间参数，幅度参数，频率参数和相位参数，以及由此衍生出的参数，比如脉冲间的幅度差异、频率差异及相位差异等。

对于上升/下降时间、脉宽、周期、平均功率、顶降等时间和幅度参数，只要得到脉冲包络波形便可以加以确定，可以通过宽带功率探头直接进行测试。

如果要测试频率和相位，则需要借助于宽带信号分析仪，采集一定宽带的信号并进行IQ分析。

为了同时兼顾雷达探测距离和距离分辨率，通常采用脉冲压缩技术，脉内采用了一定的频率和相位调制，常见的调制方式包括chirp pulse、barker code pulse等。对于这类信号的分析，则需要评估其频率和相位参数。

当然，信号分析仪可以自动完成频率和相位参数的分析，下面关于IQ数据处理的一些基础知识仅供参考。

根据IQ数据，并按照如下公式，便可以计算出信号的幅度、频率和相位信息。

I(k)和Q(k)分别为第k个样点的I值和Q值，Ts为采样时间间隔。

当计算出每一组IQ样点对应的幅度、频率和相位时，便可以得到它们随时间的变化趋势，从而完成信号瞬态过程的分析。

射频脉冲信号的相位噪声

最简单的射频脉冲可以采用图3所示的方式产生，基带脉冲控制开关的通断，输出的信号时有时无，变形成了射频脉冲。这本身也是一个调制的过程，从时域看，是基带脉冲与CW信号相乘的效果，在频域相当于发生了卷积。

频域卷积的过程，也是频谱搬移的过程，基带脉冲的每一根谱线都被搬移至射频频段。与此同时，CW信号的相位噪声也会调制到每一根谱线上。

图3. CW与基带脉冲相乘得到射频脉冲信号

观测射频脉冲的线状谱，中心载波的相噪将是所有谱线的相噪叠加的结果，因此，其相位噪声要比CW信号的相噪差。

射频脉冲的相噪测试，最大频偏通常限定在PRF/2，PRF为脉重频。为什么有这个限定呢？

PRF/2刚好是中心载波与右侧第一根谱线之间的中心距离，两根谱线之间的相噪主要由这两根谱线的相噪决定，在[0, PRF/2]范围内的相噪以中心载波为主，在[PRF/2, PRF]范围内的相噪以另一根谱线为主，因此，为了准确评估中心载波自身的相噪，故对最大频偏有此限定。

另外，脉冲时间参数不同时，比如不同的脉宽和占空比，测得的中心载波的相噪也将不同，并不是测试有问题，而是脉冲调制的固有特性，本质上还是各个谱线的相噪叠加的效果。