电子发烧友App
说到射频PA（Power Amplifier，功率放大器）的设计和应用，有两个名词经常被大家提及：Load-line与Load-pull。在使用中，这两个名词太过常用了，以至于对这两个名词后面的理论依据反而讨论不多。接下来我们就对Load-line和Load-pull背后的知识做一个讨论。
Load-line：负载线，PA的生命线
Load-line中文名称为负载线，是PA设计中最为重要的设计参考。
对于PA来说，最重要的目的是进行功率有效的放大与输出，一切的设计理念均是为此服务。此时，以最大功率“传输”为首要目标的共轭传输无法完成最大功率“输出”的目的：PA需要实现的是将射频功率最大程度的从直流功率中榨取出来，而不是将已经产生的信号传输出去。 实现射频功率最大化输出用到的就是“最佳负载匹配”，而不是用来最大化传输已有功率的“共轭匹配” 。
为了直观分析PA在不同负载下的功率输出，在PA设计中就引入了“负载线（Load-line）”的概念，用以观测PA在不同负载下的射频电压与电流摆幅，从而得出不同负载下的功率输出，找到最佳负载。
1.晶体管的DC-IV曲线
PA工作是基于晶体管的特性工作的，所以在讨论PA的Load-line之前，首先对晶体管特性做一个分析。
PA可以采用HBT、MOSFET、pHEMT等多种半导体工艺进行设计，不同工艺设计在PA的Load-line理论中分析方法基本相同。以下将以射频PA中最为常用的HBT（Hetero-Junction Bipolar Transistor, 异质结双极型晶体管）器件为例进行分析。
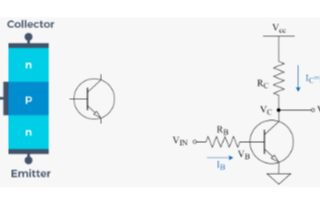
HBT是一种特殊的BJT（Bipolar Junction Transistor，双极型晶体管），由两个背靠背连接的PN结构成。下图为HBT器件与其所设计的放大器的基本结构。
图：HBT器件及共发射极放大器基本结构
对于HBT器件来说，由于Base的小电压（或电流）可以对Collector的大电流进行控制，所以一个小的Base输出信号，就可以经由HBT器件在Collector产生大的输出信号，这就是HBT作为放大器的基本原理。
理想情况下，HBT器件在工作中有以下几个特点：
- V
CE要足够的大，才能建立起CE之间的电流 - V
CE足够大之后，ICE不受VCE控制，只受Base电流IB控制 - I
CE与IB呈β倍关系
简单起见，为了理解这种控制关系，可以把HBT器件理解为一个水龙头，Collector是水龙头的输入，Emitter是水龙头的输出，而Base是水龙头的控制：
- 水压要足够大，水龙头才可以有水流出（V
CE要足够大） - 一旦水压足够大，水龙头的出水量就不再由水压控制，而是由控制龙头Base控制（I
CE不受VCE控制，只受Base电流IB控制） - 出水量与龙头控制间有一个比例关系（β倍）
将HBT器件在不同的VCE电压及不同的IB控制下的ICE在直角坐标系中描绘出来，就得到HBT器件的DC-IV曲线（直流DC状态下的电流电压曲线），DC-IV 曲线是半导体器件中的重要特性曲线 。
图：将HBT器件理解为“水龙头”；HBT器件的DC-IV曲线
2.放大器的Load-line
实际放大器在工作中，需要驱动负载阻抗。放大器对负载阻抗的驱动作用以及其小信号电路等效如下图所示。在小信号等效电路中，HBT可以等效为电流控制电流源。
图：带有负载的放大器基本电路及其小信号等效模型
考虑负载
后，在满足欧姆定律的条件下，
点电压与电流的相互转换以电阻为斜率进行相互转换。将这种转换关系对应到前节所述DC-IV曲线上，就得到一根斜率为
的直线，这根线****就 称之为此时放大器的Load-line 。Load-line的斜率与负载呈反比，中文称为负载线。
图：输出电压与电流摆幅关系及Load-line
3.Load-line与输出功率间的关系
Load-line之所以重要，是因为其直接决定了放大器最大输出功率。
为了分析Load-line与输出功率的定性关系，在手算直观分析中，一般以A类放大器进行简化分析。B类、AB类等放大器结论相同，不过分析过程更为复杂，若考虑到谐波阻抗、负载阻抗虚部影响，就需要借助仿真软件仔细分析。
对于匹配到最佳负载的功率放大器来说，最大输出功率时其电压与电流摆幅均达到最大，交流峰值分别等于为
，此时放大器的输出功率
可以有多种表达方式，如：
此时：
并有关系：
由于在此负载线下，放大器有最大的输出功率，所以此负载线又叫放大器的最佳负载线:
。对于某5G PA，以
电压为例，若目标输出功率为34.5dBm (2.82W)，则此时的最佳值Load-line在：
当
远离时，需要分两种情况进行讨论，分别为＞（高Load-line）及＜（低Load-line）。
**当 **
＞时，将此时负载线记为
。当电压达到满摆幅时，电流并没有达到满摆幅。此时输出功率受限在电压摆幅上，所以输出功率只能以电压摆幅计算，即：
图：＞时的负载线
当 
＜时，将此时负载线记为
。当电流达到满摆幅时，电压并没有达到满摆幅。此时输出功率受限在电流摆幅上，所以输出功率只能以电流摆幅计算，即：
图：＜时的负载线
4.Load-line的阻抗与匹配
通过以上分析，可以得到某5G射频PA的最佳负载阻抗约在3.1Ω左右，在设计中，需要设计匹配网络将50Ω负载匹配至该目标负载阻抗。输出匹配网络在放大器中的位置与基本结构如下图所示：
图：5G PA的输出匹配网络
输出匹配网络将较高的50Ω阻抗匹配至较低的负载阻抗3.1Ω，可以证明，一个匹配网络的损耗和转换网络的Q值（
）成正比，和器件的Q值（主要为电感Q值
，以25作为估计）成反比，即：
若采用单级L-C匹配网络，则50Ω到3.1Ω的损耗为15.6%，即0.74dB。
在转换比过大时，可采用多级匹配的方式减小损耗。比如采用两级匹配的方式进行匹配，若将50Ω先匹配至12Ω，再匹配至3.1 Ω，则两级匹配网络的损耗分别为7.1%及6.8%，整体损耗为13.4%，约0.63dB。
5. ** “高Load-line”与“低Load-line”PA**
由于输出功率是由
与两个参数共同决定，所以在设计时可以采用高与高的方式（即高Load-line），也可以采用低与低的方式（即低Load-line）进行设计。
采用低压（配合低Load-line）方式设计的PA优势显而易见：更低工作电压使得供电只需要Buck电路， 不用 Boost，这样供电电路会简单并且电源转换效率更好。 虽然对于同样的输出功率来说，电压降低后电流会升高，但二者乘积相同，总功耗相同。
低压PA虽然优势明显，但对设计的挑战增大。低压PA所使用的Load-line较低，匹配网络进行转换时匹配网络的Q值变大，损耗增加。下表列出了采用4.2V设计时Load-line为3.1Ω，以此为标准，输出功率相同时，3.4V低压PA的Load-line为2.0Ω，损耗增加0.08dB，此额外损耗需要在设计中予以克服。对此损耗的克服一般通过优化PA设计可以实现。
随着电压再降低，输出匹配网络损耗快速增加，所以Load-line不能一直降低。另外，低压使用时，器件本身所占用的膝电压（
，Knee Voltage）占的比重开始增加，进一步限制电压摆幅，影响输出功率。
图表：同输出功率，不同电压及Load-line下，
所对应的匹配网络损耗
6. 实际应用中的Load-line
- 以上分析采用简单Class A PA进行简化分析，在实际应用中手机PA通常用Class F，Class AB，ClassE, 和 Doherty等。这些PA需要的最佳负载可能是复数，并且需要考虑谐波负载，负载线的表现与Class A PA会有不同；
- 以上分析中，最佳负载线根据最大功率进行设计，通常PA设计需要综合考虑PAE与ACLR等其他指标；
- 另外，最佳负载匹配网络需要综合考虑阻抗变换比/网络元件Q/频率带宽三个要素。
Load-pull：负载线理论的最佳实践
虽然Load-line理论可以对PA特性进行简单清晰的分析，但在实际使用中，由于阻抗并非只有实部，并且加入导通角、匹配网络以及谐波影响后会变的非常复杂。Load-line理论对于清晰理解PA的设计思路很重要，但在实际设计与应用中显得心余力绌。
于是，Load-pull的概念被引入了进来。
说起Load-pull，射频人都不会陌生：在每本教科书里都会提到；Load-pull在Smith圆图上的等高线（Contour）也是PA设计和应用中的必备材料。下图为典型的Load-pull在Smith圆图上的结果呈现。
图：典型的Load-pull结果在Smith圆图上的呈现
相比于“Load-pull”名字的熟悉，大家对它背后的理论谈论较少。Load-pull的测试过程也像是“暴力破解”，好像没什么理论可依。
不过实际并非如此，Load-pull背后有详细的理论分析，PA届的大神Cripps于1983年发表的IEEE MTT-S的论文“A theory for the prediction of GaAs FET Load-pull Power Contours”[2]就曾用纯理论的方式对PA的Load-pull进行预测。通过测试验证，Cripps的理论预测完美的匹配了测试结果。
图：Cripps在1983年对PA Load-pull进行的理论预测及验证
接下来，就让我们沿着Cripps的思路，仔细理解Load-pull。
1. 什么是Load-pull
Load-pull的中文名翻译为“负载牵引”，是指将被测器件（DUT，Device under Test）的负载阻抗进行遍历，同时测试记录不同负载阻抗时的器件特性，从而得到最优阻抗的方法。
在CAD仿真软件中，Load-pull结果的获取较为容易，只需要将DUT的负载进行扫描，就可以绘制出多种多样的Load-pull图形，通常几秒中，就可以将Load-pull结果扫描出来。下图为使用ADS软件进行Load-pull仿真以及得到的结果 [3]。
图：采用ADS软件仿真得到的Load-pull结果
在实际测试中，想要精准的遍历各个阻抗就不如仿真中容易了，需要借助Tuner（阻抗调谐器）来实现负载阻抗的控制，Tuner也是整个Load-pull系统中最为重要的组成部分。Tuner可以理解为阻抗调谐匹配单元，可以将固定的负载阻抗有控制的匹配至Smith圆图上的其他位置。Load-pull测试系统的原理图及实际测试系统如下图所示[4][5]。
图：Load-pull测试系统原理图 [4]
2. Load-pull理论
通过对PA的仿真或测试，可以得到不同负载下PA不同输出功率的等高线图。为何PA输出功率会呈等高线形状，另外等高线形状是圆形吗？等高线一定是闭合的吗？接下来将进行详细讨论。
2.1 实阻抗在Load-pull中的表示
通过Load-line理论，可以得到PA负载在最佳负载线（
，以下以
表示）时有最大的输出功率。将此时的表示在Smith圆图上，就得到Load-pull的中心点。
同理，对于高Load-line时的负载
及低Load-line时的
，同样可以在Smith圆图上标注出来。及处分别电压及电流受限，功率均小于处功率。
图：Load-line的负载与Load-pull的阻抗标注
2.2 高Load-line区：电压受限；等电导圆上功率不变
在高Load-line区，Load-line阻抗大于最优负载阻抗，Smith圆图表示为在的右侧。此时电压摆幅受限，输出功率以最大电压摆幅计算，为：
由于电压固定，当输出带有虚部时，采用并联等效电路进行功率计算更为方便，将此时负载电路等效如下：
图：用于电压驱动时的负载并联电路等效
此时，
的最大值保持恒定，峰值为
。若电导
也保持一致，则输出功率恒定为：
即在高Load-line区，在等电导圆上输出功率恒定一致 **。**此时电压电流波形及在Smith圆图上的阻抗位置如下图所示。
图：高Load-line区域时，虚部增加对电压电流波形的影响
需要注意的是，当负载阻抗在远离向短路点移动时，虽然电压摆幅保持一致，但电流摆幅会逐步增加。若电流摆幅增加至
，则电流开始受限，不能再使用前述电压与的方式计算功率，即功率无法保持恒定。有关电流达到受限的阻抗点后续将详细讨论。
在此讨论另外一个现象：当负载阻抗沿等
圆移动时，可以看到电流摆幅明显增加。为何电流摆幅增加不会带来功率的增加呢？欢迎大家留言，讨论对此现象的理解。
2.3 低Load-line区：电流受限，等电阻圆上功率不变
在低Load-line区，Load-line阻抗小于最优负载阻抗，Smith圆图表示为在的左侧。此时电流摆幅受限，输出功率以最大电流摆幅计算，为：
当输出带有虚部时，由于电流受限，采用串联等效电路进行功率计算更为方便，将此时负载电路等效如下：
图：用于电流驱动时的负载串联电路等效
此时，
的最大值保持恒定，峰值为
。若电阻
也保持一致，则输出功率恒定为：
即 在低Load-line区，在等电阻圆上输出功率恒定一致 。此时电压电流波形及在Smith圆图上的阻抗位置如下图所示。
图：低Load-line区域时，虚部增加对电压电流波形的影响
与高Load-line区域分析类似，在此时同样要注意，随着负载阻抗远离
向开路点移动时，电压摆幅也会逐步增加，直至电压受限。也同样可以讨论：为何电压摆幅的增加，没有带来功率的增加？
2.4 有关“受限”的讨论
在以上分析中，高Load-line区域电压受限，但当负载沿等
圆移动时，电流摆幅增加，直至受限；低Load-line区域电流受限，但当负载沿等圆移动时，电压摆幅增加，直至受限。这个受限点在哪里呢？
对于高Load-line区域，设
，则在等圆上，输出功率以
表示，为：
此时，输出功率为最大输出功率的1 /A 。
在低Load-line区域，若得到与此相同的输出功率，根据
可得低Load-line区域的阻抗点阻抗 
。
计算高Load-line区域沿等圆变化时电流随阻抗实部的变化。此圆上的电流及阻抗实部分别以
及
表示，以电流及阻抗的方式计算等圆上的输出功率为：
令其与电压、导纳计算方式得到的功率相同，则：
即：
当电流摆幅达到最大，即
时：
即：在当等
圆与等
圆相交时，电流取到最大值，电流与电压同时受限。此时用Smith圆图表示的Load-pull曲线闭合，等功率圆呈现橄榄球形状的闭合曲线 。
当Smith圆图上的阻抗远离
时，输出功率变小。所以，Smith圆图上的等功率圆呈现出一组闭合的等高线。
图：Load-pull曲线的闭合，以及Load-pull的等高线结果
3. 实际中的Load-pull
在实际应用中，观测到的Load-pull曲线和理论分析曲线可能存在差异，有以下几点需要注意：
- 匹配网络可能将Load-pull结果进行转移
- 谐波会影响Load-pull结果
- 以上为等功率圆，实际应用可能是等ACLR圆、等PAE圆，并且信号为带有带宽的调制信号
3.1 匹配网络对Load-pull的转移
以上分析均是以PA晶体管输出平面计算，由于匹配网络及寄生效应的影响，在芯片输出端口观测到的Load-pull可能会有不同。以下为不同平面看到的不同Load-pull示意图。
图：PA电路中不同平面观测到的Load-pull形状不同
3.2 谐波对Load-pull影响
以上分析中均为简化分析，只考虑基波（Fundamental）阻抗的影响，在PA设计中，其他高次谐波，如2f0、3f0等阻抗均会对PA功率、效率以及线性度产生影响。考虑谐波影响，Load-pull形状会有差异。
3.3 其他指标的Load-pull
以上分析针对PA中最为重要的指标：功率的Load-pull进行分析，PA的其他指标如线性度等，采用带有带宽的调制信号进行测试，其Load-pull形状大致相同。一般不会再针对其他指标进行详细分析。
**总 结 **
Load-line与Load-pull是PA设计中最重要的两个基础概念，在过去几十年的射频PA设计中，前人专家也积累了许多经典的分析方法。
虽然5G等高阶通信协议的到来对射频PA提出了新的要求，近年来也涌现出如低压PA、高效率PA、高/低Load-line PA等不同PA产品，但射频PA的一些基础原理仍然是在PA设计中被广泛遵循的，期待和您一起对这些基础原理有更好的理解。
工商网监
评论