使用相控阵进行数字和模拟波束成形的基础知识
AuthorCadence System Analysis
第一台相控阵雷达是由德国物理学家卡尔·布劳恩于1905年发明的,带有三个发射器。从那时起,雷达在各个层面都变得更加先进。在系统尺寸、发射器数量、信号处理、线性调频应用和可用组件方面,相控阵设计人员比以往任何时候都更容易设计先进的波束成形系统。执行波束成形的两种主要方式是数字和模拟,对于需要波束成形的系统,每种方法都有其优势。
当今在毫米波频段和更高频段运行的先进无线和传感器系统使用波束成形。这适用于较新的WiFi标准,LTE和较新的无线迭代,当然还有雷达。在本文中,我们将了解模拟波束成形如何主导RF通信,以及设计如何转向数字波束成形模型以支持实现MIMO的系统。
相控阵波束成形的概念
波束成形遵循一个简单的概念:塑造从天线发射的电磁能量的空间分布,使其沿特定方向定向到目标。相控阵是用于实现模拟波束成形的标准天线结构,这是迄今为止占主导地位的波束成形方法。通过协调阵列的发射,发射电磁辐射的叠加从天线阵列获得的增益比从单个天线获得的增益更大。
引导来自相控阵的广播信号有两种主要方法:模拟波束成形和数字波束成形。前者是众所周知的,早在无线通信开始采用波束成形之前,它就已经用于最好的雷达系统。
模拟波束成形
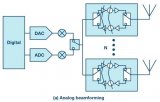
在模拟波束成形中,单个输入数据流(由调制RF信号表示)被提供给一组通向相控阵的馈线。在此过程中,有意对通向每个天线的输入信号施加相移。发送到每个天线的广播信号之间的相移将决定发射波束的方向。
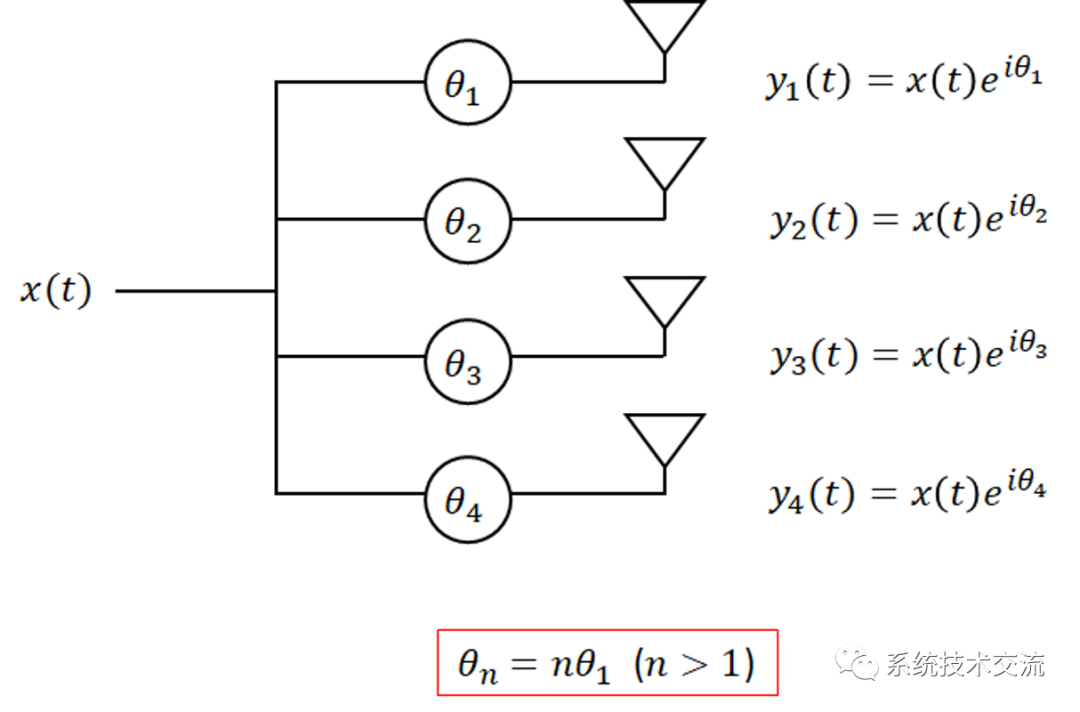
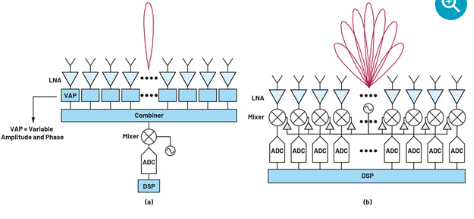
具有 4 个 Tx 天线的模拟波束成形架构示例。
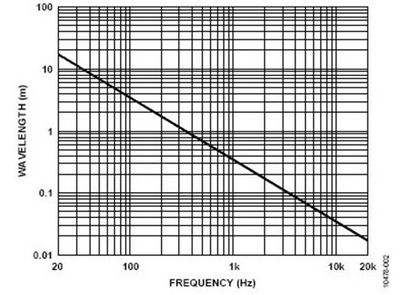
当封装在PCB上时,这些天线通常间隔为广播波长(空气中的值)的几倍。像雷达这样的系统将共同定位Tx和Rx元素,Rx元素将以互惠的方式作为Tx元素运行。为了确保最小的串扰和噪声抑制,通常使用共面波导路由将信号路由到天线元件中。
模拟波束成形通常非常适合波束数低的低成本系统。随着系统物理大小的增长,这带来了可扩展性挑战,这是可取的,原因如下:
更多天线元件提供更高的增益
更多的天线元件可以提供更窄的波束宽度,在成像等应用中提供更高的分辨率
更多的antenne元件允许实现更多的无线信道(例如,MIMO)
在具有高天线数量的RF系统(例如,雷达和5G产品)中,需要以更高的频率工作,因为它允许使用物理上更小的天线。模拟波束成形的可扩展性挑战来自于所有收发器和所有辐射元件的相位同步需求。随着系统尺寸的增长,使用低频振荡器控制相位差和直接光束变得更加困难。这是模拟波束成形中使用的级联收发器面临的一个已知挑战。
数字波束成形
数字波束成形是一个较新的概念,可以克服模拟波束成形系统在高级应用中的可扩展性限制。特别是,具有多用户MIMO(MU-MIMO)的数字波束成形用于LTE传输模式7-9和5G NR。成像雷达是模拟波束成形的另一个领域,由于形成高分辨率图像需要大量发射器,因此模拟波束成形开始变得不可扩展。
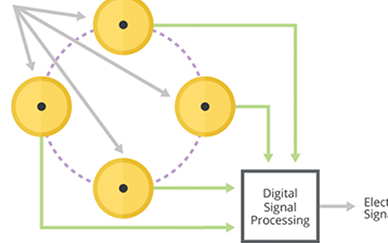
在数字波束成形中,每个天线元件都有一个专用的ADC。结果是可以同时采集和传输多个波束,而无需精确的相位控制来实现波束成形和转向。而不是取决于数据流之间的相位差的光束转向角,使用一种称为预编码的技术来组合光束,以便它们从所有元素叠加发射同时沿多个所需路径产生光束。
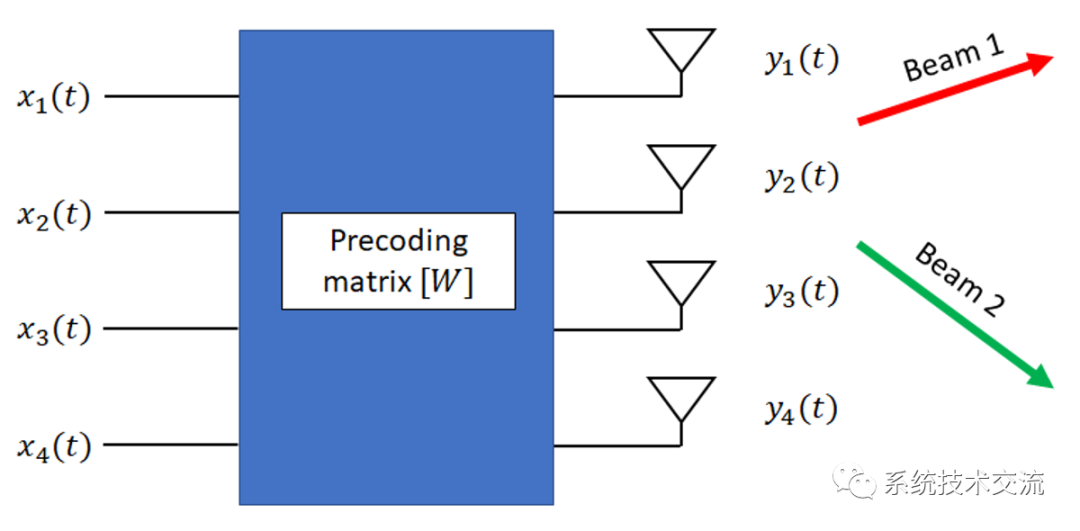
具有 4 个 Tx 天线的数字波束成形架构示例。
这需要根据通道状态信息 (CSI) 计算预编码矩阵 [W]。这还必须在非常短的时间间隔内重复完成,以便能够使用定向波束进行重复无线传输,以提供高吞吐量的数据传输。该矩阵将输入信号与广播信号相关联,如下所示:
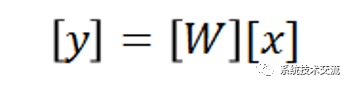
如果所需的输出波束模式已知,则可以反转以确定广播信号,然后反转以确定所需的输入信号。
此选项使用更多的功率,成本更高,并且完成PCB布局可能更加困难。有一种折衷方案可以提供两全其美的方法:混合波束成形。
混合波束成形:更先进的系统
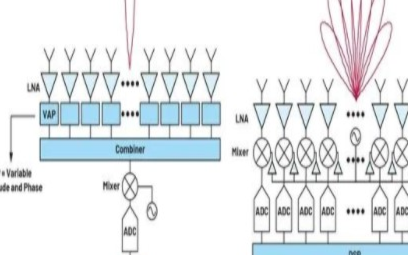
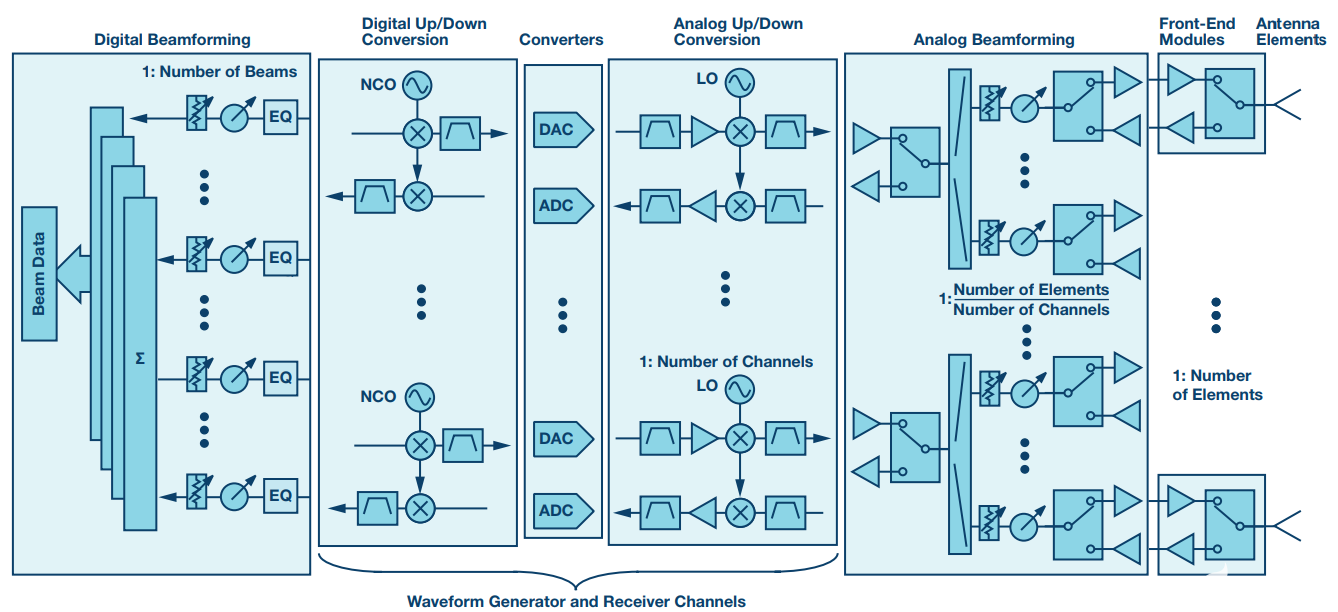
一种涉及模拟和数字波束成形的更高级技术是混合波束成形。在这种方法中,子阵列由非常大的阵列形成,子阵列中形成的波束使用模拟波束形成进行控制。
每个子阵列可以共享一个ADC,即系统在此概念中使用模拟波束成形阵列的数字阵列。混合波束成形在需要数字波束成形的应用中很受欢迎,但由于尺寸限制和功率限制,全数字波束成形可能不可行。示例体系结构如下所示。
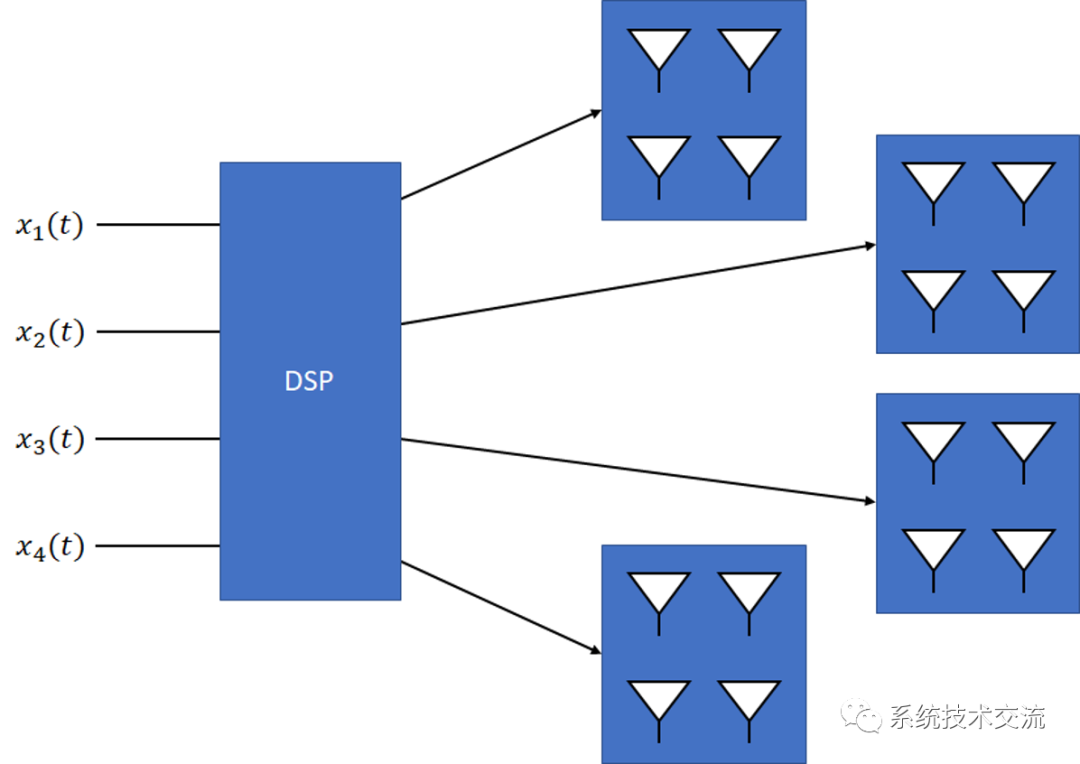
混合波束成形中使用的 4x 子阵列的系统架构示例。
这种架构需要在多个层面进行仔细设计:信号处理、PCB布局、元件选择和数字子系统实现。上面显示的示例只是将系统划分为子阵列的一个例子,但这并不是对数字波束成形有用的唯一方法。其他架构可用于混合波束成形系统。
PCB布局部分可能特别具有挑战性,因为它仍然需要模拟波束成形中使用的相位同步,但这与将数据流发送到子阵列所需的多个高速通道一起工作。其他混合波束成形表现形式也有可能帮助克服模拟和数字波束成形中的可扩展性挑战。
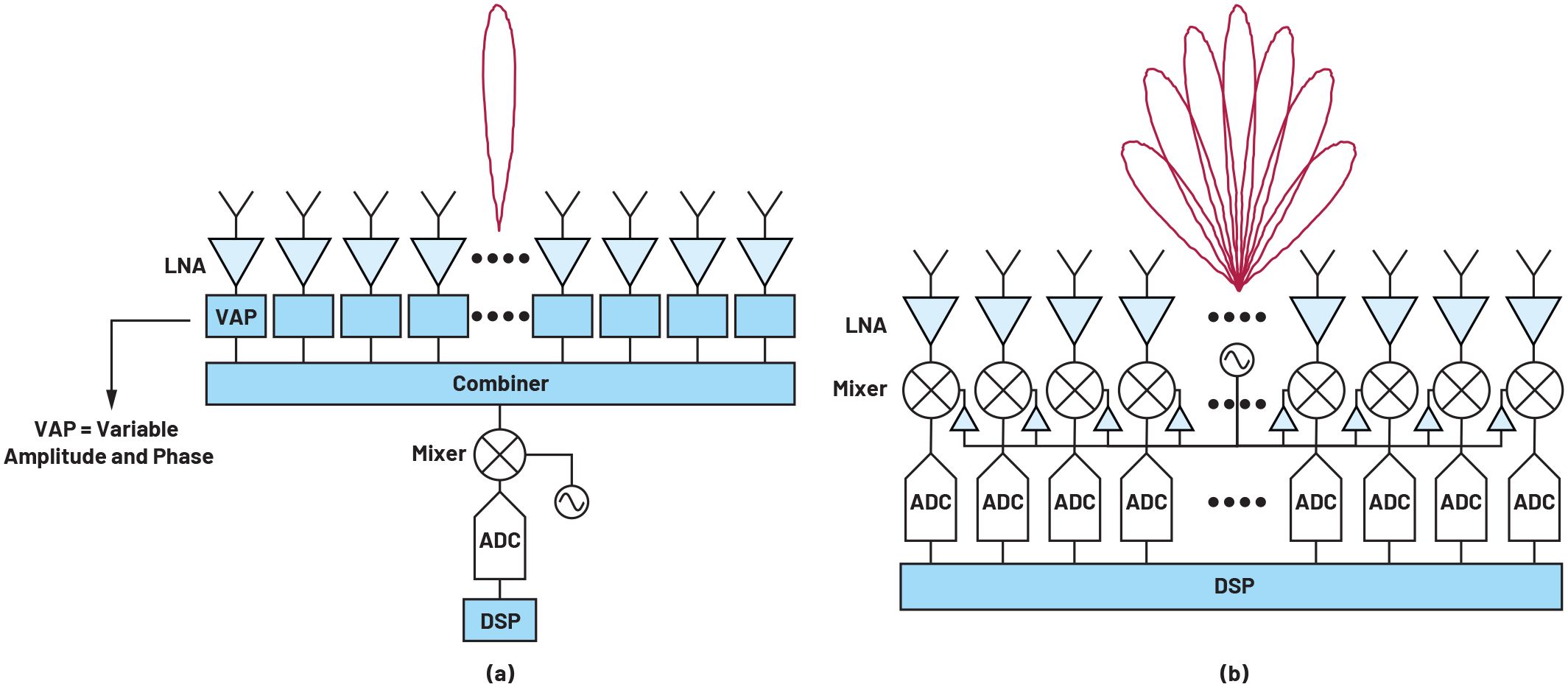
波束成形用于定向信号发送和接收。它具有改变幅度和相位的规定,这有助于 功率变化以及分别在所需方向上的波束转向。单独提供幅度/相位变化的天线阵列是 用于发射和接收的波束成形。
在模拟波束成形中,幅度/相位变化应用于发射端的模拟信号。在ADC转换之前对来自不同天线的信号进行汇总 在接收端的模拟波束成形中。
在数字波束成形中,在发射端进行DAC转换之前,对数字信号施加幅度/相位变化(Wk)。反向过程是在执行ADC和DDC操作后完成的。如图所示,来自天线的接收信号首先从ADC转换器传递,然后 求和操作前的数字下变频器(即DDC)。
模拟波束成形
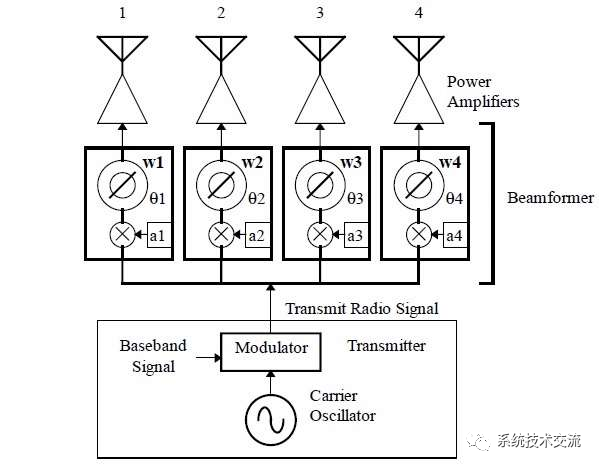
图1描绘了模拟波束成形发射器。如图所示,要传输的基带信号为 先调制。该无线电信号使用功率分配器进行分离,并通过波束成形器,波束成形器具有 规定改变振幅(ak) 和相位 (θk) 的信号 在通往天线堆栈的每条路径中。功率分配器取决于使用的天线数量 例如,在天线阵列中,需要4路功率分配器来满足4天线阵列的需求。
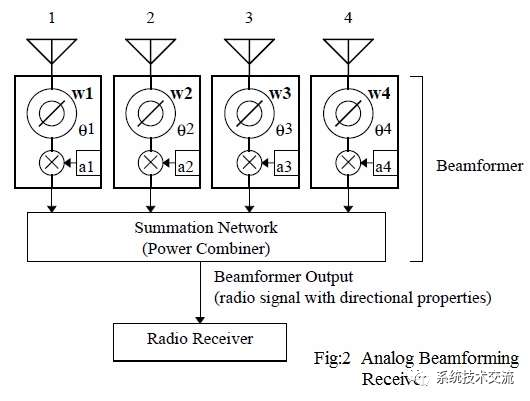
图2描绘了模拟波束成形接收器。如接收器框图所示,复数权重应用于 来自阵列中每个天线的信号。复权重由振幅和相位组成。完成这些操作后,信号将组合成一个输出。这提供了天线阵列所需的方向图。
Wk= ak*ejsin(θk)
Wk= ak*cos(θk) + j* aksin(θk)
其中,
Wk表示阵列中第 k 个天线的复数权重。
一个k是重量的相对振幅。
θk是重量的相移。
数字波束成形
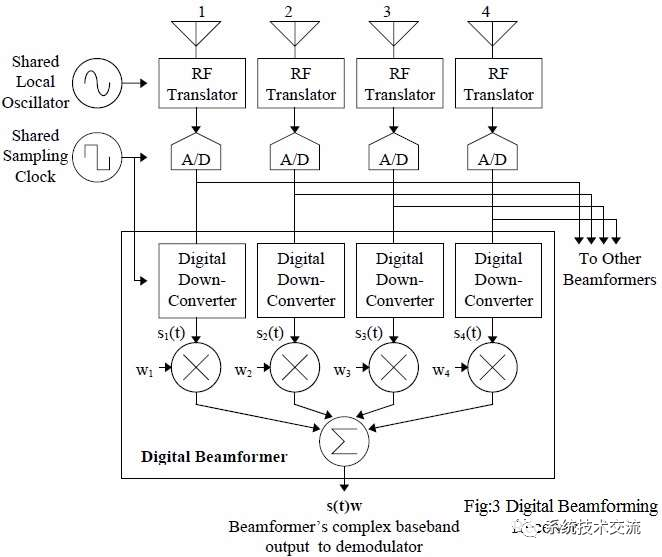
图3描绘了数字波束成形接收器。如图所示,每个天线元件的幅度缩放、相移及其总和 已以数字方式进行。
• 数字波束成形由射频转换器、A/D 转换器、DDC、复权倍增组成 和求和操作。
• 射频转换器将较高的射频信号频率转换为较低的中频 信号频率。这是使用RF混频器完成的。LO信号被馈送到RF混频器 为了执行射频到中频转换。适当的滤波器(带通和低通)是 用于RF混频器的输入和输出。
• 此IF信号使用A / D转换器转换为数字等效值 适当的采样时钟。
• 数字化的IF信号被传递到DDC(数字下变频器)。
• 这些天线元件的结果总结为 产生具有所需方向模式的基带信号。
• 求和后的信号被交给解调器 从无线电信号中检索信息。
下表提到了模拟波束成形和数字波束成形之间的区别。
| 模拟波束成形 | 数字波束成形 |
|---|---|
| 射频处的自适应发射/接收权重以形成波束 | 基带自适应发射/接收权重 |
| 一个收发器单元和一个具有高天线增益的射频波束 | 每个天线元件或天线端口都有一个收发器单元,高数 (>8) 收发器单元。 |
| “频率平坦”波束形成 | “频率选择性”波束形成 |
| 最适合覆盖范围(由于低功耗和成本特性) | 最适合容量和灵活性(受高功 |
模拟波束成形
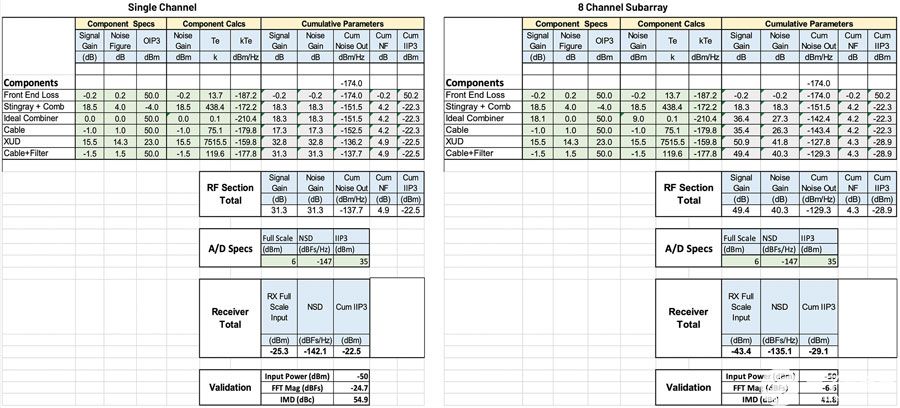
模拟波束成形(ABF)是指从相控阵天线的每个元件接收到的回波信号, 在射频载波频率级别进行组合。这款模拟波束成形器最多可馈电四个 集中式接收通道,将信号下变频至基本频段 (或中频,如果)。以下模数转换器 (ADC) 数字化IF或视频信号。
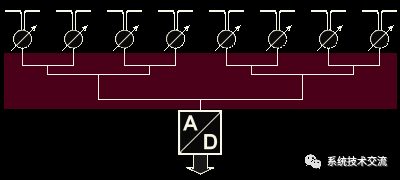
数字波束成形
数字波束成形(DBF)可以在天线元件级别或子阵列级别实现。在DBF架构中,有许多数字接收器, 天线的每个辐射元件上都有一个自己的接收器。下变频至中频并将信号数字化 在每个单独的天线元件(或其中的一小群)上实现。每个接收器中的噪声和信号失真在所有接收器之间是去相关的。
数字波束成形处理器中可以形成多个向各个方向控制的独立波束。数字波束成形的优势包括:
改进的动态范围;
控制多个光束;
更好、更快地控制幅度和相位。
标准化模块化发送/接收模块 (SMTR)
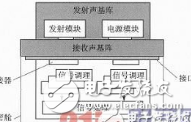
发送/接收模块是基于AESA技术数字波束成形的关键组件。这些模块包含发射器功率放大器的一部分和接收器的一部分 并且可以批量生产,以实现更好的性价比。这些模块可用于各种程序,只需稍作个别调整。通过紧凑的设计,信号处理过程中的线路损耗很低。例如,标准化的模块化发射/接收模块用于中型扩展防空系统的X波段多功能火控雷达 (米兹), 在德国武装部队地面监视雷达BÜR,TerraSAR-X太空雷达以及欧洲战斗机的E-Captor雷达中。
SMTRM是一种密封覆盖的电路板,尺寸 长度为64,5毫米,宽度为13,5毫米,高度为4,5毫米。该板包含一个功率放大器,其形状为两个单片集成电路,馈送不同的相移,一个铁氧体环行器,用于将发射器/接收器连接到发射/接收路径, 单片集成限幅器和低噪声前置放大器。接收到的信号将被下变频为中频。所有电路均采用砷化镓(GaAs)半导体技术进行。
波束成形处理器
这种同时组织各种天线模式的能力只有成为可能 采用数字接收器技术 因为只有数字信号可以复制任意次数而不会丢失。实际上,接收到的信号被转换为中频,然后立即数字化。当IF为75 MHz时,模数转换器需要100 MHz的采样频率。
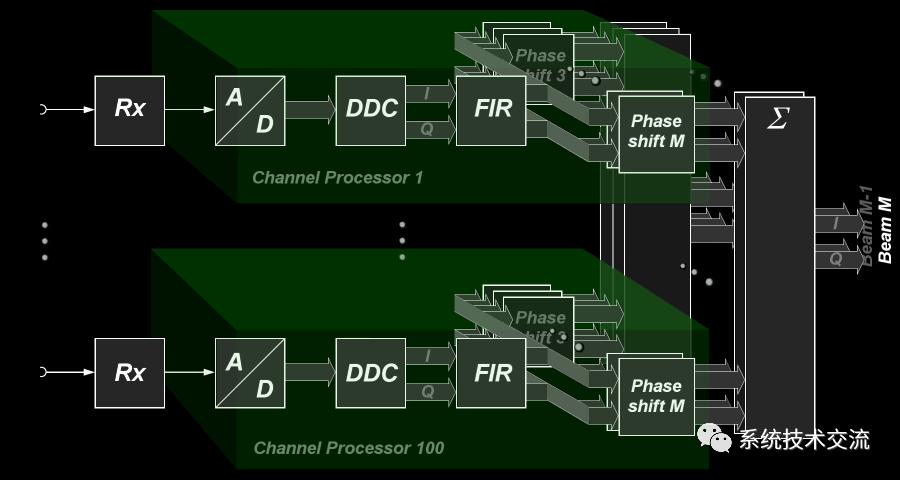
图4显示了典型波束成形处理器的框图。相控阵天线的每个天线都有自己的接收通道 其次是自己的模数转换器和数字下变频器(DDC)。为了正确求和,有一个特殊的横向滤波器 这均衡了频率响应并校正了该接收通道中的单个传播延迟。这种横向滤波器也称为有限脉冲响应滤波器(FIR)。它被调谐到一个特殊的自动校准程序。对于此校准,已知的RF测试信号将被馈入接收器通道, 它要么是在整个带宽上调制的线性频率),要么是具有已知幅度的白噪声。该滤波器中还制作了抑制旁瓣所需的权重。接收通道的所有模数转换器的数据都以复数形式馈送 (I&Q)信号通过任何求和级的移相器级。求和级数决定了可能同时接收的天线波束的数量。在图中,假定求和级数为 100。
提高灵敏度
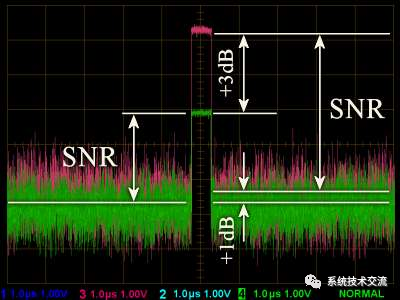
每个单独的接收通道都有一个可比的信噪比(SNR) 使用模拟波束成形到雷达接收器中的接收路径。然而,噪声是一个混沌的过程,必须在两个接收通道中有所不同。因此,两个不同接收器中的单个噪声峰值不太可能相同, 虽然这不能完全排除。
因此,如果两个接收通道在相位上相加,则回波信号总和为更大的脉冲, 但是噪声是去相关的,相位和幅度不匹配。因此,噪声的总和不能与回波信号相同。即使有两个接收通道的总和,这也将信噪比提高了约2 dB, 导致使用数字波束成形的雷达灵敏度更高。在 37 个接收模块的配置中(如雷神公司的可扩展防空和导弹防御雷达 AMDR), 这导致在实践中灵敏度提高约15 dB。
现代雷达以数字方式执行几乎所有所需的信号处理。最常用的数字信号处理技术是快速傅里叶变换(FFT)。在雷达数据路径中,该算法用于波束成形、脉冲压缩和多普勒处理等领域。首先,下面简要介绍FFT。
快速傅里叶变换
FFT技术只是离散傅里叶变换(DFT)的高度优化实现。FFT和DFT产生相同的结果,但与DFT相比,FFT需要的计算工作量很小。
离散傅里叶变换
DFT是对采样数据(信号)的输入序列的转换,产生该采样数据序列的频率内容或频谱表示。这将给出信号在频域中的表示。
逆离散傅里叶变换
还有一个逆离散傅里叶变换(IDFT)和一个逆快速傅里叶变换(IFFT)。同样,IFFT只是IDFT的优化形式。它们都根据频域信息计算信号的时域表示。使用这些变换,可以在时域信号和频域频谱表示之间来回切换。
DFT在长度为N的复输入数据序列“xi”上执行。要使用计算效率更高的FFT,N的长度必须为2 n,其中n是任何正整数。小于此长度的长度可以零扩展到下一个 2n 长度。复数输出序列 “Xk” 的长度也是 2n。DFT将采样时域信号(xi)转换为采样频域(Xk)频谱表示。因此,它不是从 –π 到 π 连续计算采样频率 ω,而是在 2π 的间隔内在 N 个等距点进行计算。索引 i 和 k 都将从 0 运行到 N -1。
DFT 和 IDFT 变换方程
DFT 和 IDFT 方程都是 N 个复指数的总和。如下所示,这些等式似乎非常相似:
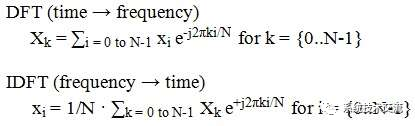
直观地说,DFT的作用是将输入数据样本与N个等间距的频率信号相关联。频域表示 Xk 只是这些相关性中每个在幅度和相位上的权重。如果输入信号不存在任何特定频率,则生成的相关性将为零,并且该频率的Xk值为零。因此,Xk的值给出了信号中每个频率分量的幅度和相位。
DFT vs. IDFT
DFT 和 IDFT 方程中的唯一区别是 DFT 方程指数上的负号和 IDFT 方程的因子 1/N。请注意,DFT方程使用每个时域样本来计算每个频域样本。IDFT方程要求使用每个频域样本来计算每个时域样本。
因此,要计算任一变换的单个样本,需要 N 个复数乘法和加法。要计算整个转换,需要计算 N 个样本,总共 N 个 2 次乘法和加法。FFT的计算效率要高得多,如表1所示。例如,使用 1024 点序列,只需 DFT 所需工作量的 1% 即可计算 FFT。
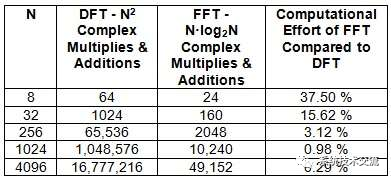
表 1.FFT 和 DFT 计算工作
同样,Xk 的值表示每个频率点的信号能量量,在采样频谱上相等间隔。由于是一个复数,它提供了每个频率分量的幅度和相位。频谱中的这些点通常称为频箱。随着N变大,频谱被分成更多的箱,频率间隔更近,提供更精细的频率区分。
什么是波束成形?波束成形是一种数字技术,可将雷达发射器和接收器聚焦在特定方向上。侧向方向通常称为方位角,上下方向称为仰角。波束成形可用于将雷达聚焦在方位角和高程上。早期的机载雷达以及许多地面和海军雷达使用图1所示的更熟悉的抛物面型天线。抛物线形状将接收和发射能量集中在天线方向上。天线可以旋转以向所有方向搜索或瞄准感兴趣的方位角和仰角。
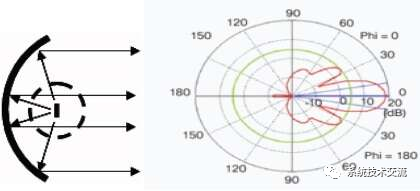
有源电子扫描阵列 (AESA)
为了搜索感兴趣的区域,天线必须机械地瞄准或旋转,以将其波束引导到所需的方向。在许多军事应用中,此功能通常使用有源电子扫描阵列(AESA)以电子方式执行,AESA是一种电子可控天线。这允许非常快速地转向雷达波束,这对于军用机载雷达特别有用。这种技术被称为“波束成形”,它参考了主天线瓣或波束的电子转向。
AESA 由许多小天线或单个元件构建而成。每个天线元件都有一个发射模块和一个接收模块。因此,每个元件可以单独改变接收和发送信号的相位和幅度。这些变化,特别是在相位上,提供了天线波束在方位角和仰角上的可控方向性。只有当接收信号同相到达所有天线元件时,才会接收到最大信号。这提供了将天线的主瓣“瞄准”到所需方向的能力。该过程是相互的,这意味着接收和发射上将存在相同的天线瓣模式(假设接收和发送的频率相同)。
每个天线元件必须具有延迟或相位调整,以便在此调整之后,所有元件都将具有共同的信号相位。如果角度θ = 0,则所有元件将同时接收信号,无需相位调整。在非零角度下,每个元件都有一个延迟,以提供跨天线阵列的波前对齐,如图2所示。一旦每个天线元件输入通过公共时钟和本振器下变频为基带,每个天线输入都会延迟正确的量,以便从给定方向到达的波前对齐。这种延迟可以通过相位旋转或乘以 W i =e jθ i 以数字方式实现。为了更好地控制旁瓣,还可以通过使用 W i = ai ·ejθ i.通过自适应地改变每个天线输入的Wi,可以实现波束成形。
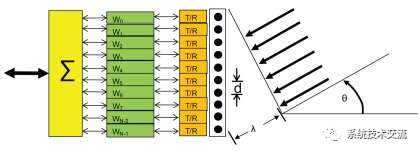
传输方向以相同的方式工作。优点是非常快速的转向,可以快速搜索和跟踪物体。可以消除机械运动和电机。使用一种称为“lobing”的技术;雷达波束可以在目标的两侧快速转向。通过注意更强的回报在哪里,可以更准确地跟踪目标运动。
FFT 波束成形
数字波束成形也可用于其他用途。在某些系统中,需要同时在不同方向上接收和传输单独的信号。这可以通过使用FFT算法来实现。通常,FFT用于获取时域信号并将其分离成不同的频率分量。在这种情况下,FFT会将输入信号分成不同的空间分量或到达角分量。输入信号由FFT分类到对应于不同到达角的箱中,如图3所示。类似地,在发射方向上,馈入每个FFT bin输入的信号将沿特定方向传输,对应于特定的天线瓣。如果FFT箱的输入为零,则不会在该方向上传输能量;发射瓣将“丢失”。
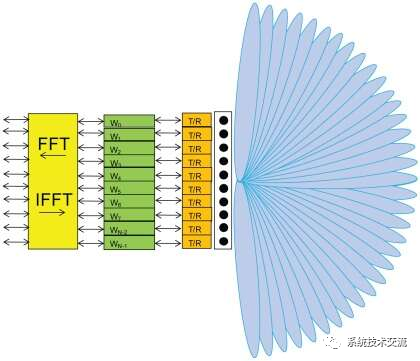
波束成形的FFT方法在计算上非常有效,允许同时接收和发送多个方向信号。这在必须同时跟踪多个目标的多模雷达中可能是一项非常有用的功能。然而,N天线波束的间距和方向是固定的,并且在方向上相等,距离天线阵列超过180度。为了与FFT的特性保持一致,任何给定天线波束的峰值正好位于所有相邻天线波束的旁瓣的零点上。这种特征被称为正交性。
脉冲压缩
接收处理的后续步骤通常是脉冲压缩和多普勒处理。脉冲压缩只是将接收信号与发射的脉冲形状进行匹配的滤波或滤波。当接收信号与发射信号完全匹配时,这种类型的滤波给出最大的响应,表明它确实是发射脉冲的反射和延迟版本(也称为自相关)。脉冲压缩和多普勒处理的顺序可以互换,但这里假设脉冲压缩首先发生,多普勒处理后发生。
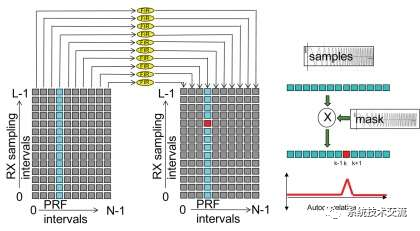
在图4中,脉冲压缩被描述为在每个PRF间隔的接收样本上执行的FIR滤波器。例如,假设雷达以 100 MHz 的频率采样,PRF 为 10 kHz。对于每个PRF,每个垂直箱中接收10,000个复杂样品。然后,每个样品箱通过匹配的过滤器。当接收到发射脉冲的反射时,这些反射将在匹配滤波器的输出中引起响应。
发射脉冲通常采用伪随机序列,可能使用相位或频率变化进行调制。伪随机或 PN 序列被设计为具有很强的自相关特性。这意味着匹配滤波器只有在接收脉冲精确匹配时才会产生输出,从而可以以同样精确的方式确定接收脉冲的到达时间。与PN序列相关或匹配也倾向于为发射脉冲以外的任何其他信号或噪声产生非常低的输出。不同的雷达应用和模式需要不同的发射波形,这本身就是一个相当大的主题。
匹配滤波器FIR功能可以在频域中实现。在这种情况下,通过FFT处理接收数据获得接收信号频谱。然后将发射脉冲的频谱屏蔽到接收信号的频率响应上。当两者匹配时,最大的反应会发生。然后使用IFFT将结果转换回时域,然后进行多普勒处理。这似乎是一个复杂的替代方案,但FFT算法非常高效,因此该方法的计算量可能低于FIR滤波。
多普勒处理
在本系列雷达基础知识的第 2 部分中,讨论了多普勒处理。在图5中,多普勒处理描绘了整个雷达数据阵列。数据列对应于每个PRF接收数据缓冲区的脉冲压缩滤波。
相干处理间隔 (CPI)
N 列数是相干处理间隔 (CPI) 中的传输脉冲数。回想一下,所有雷达数据都很复杂,具有幅度和相位。CPI 与整个阵列中数据之间的相位关系有关。随着时间的推移,RF和数字电路中使用的时钟电路、数据转换器和锁相环中的轻微时钟漂移和抖动会导致样本之间的相对相移。对于机载或车载雷达,雷达的移动也会干扰相位关系。接收数据样本经过的时间越长,相对相位退化的可能性就越大。此外,任何雷达频率模式变化或PRF变化都可能导致相位不连续。CPI是这些相位差携带有用信息或相干的时间间隔的度量,因此可用于频域处理,例如多普勒处理。它通常延伸到多个PRF时间段。
请注意,从脉冲压缩处理接收到的样本输出将加载到每个 PRF 的列中。多普勒处理跨行或跨 N 个 PRF 进行。必须在一段时间内收集数据,在该时间间隔内,数据可以被视为连贯的或在 CPI 范围内。
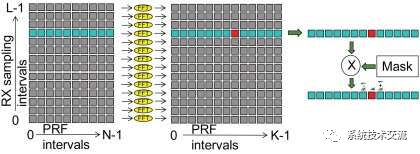
图5.多普勒处理“转角”
这种数据流在雷达方言中被称为“转弯”,因为数据垂直进入,水平出来或转弯。此处理要求在执行任何多普勒处理之前,阵列中存在所有数据。数据量可能非常大,对于高性能雷达处理,需要以非常低的延迟进行访问。这要么需要非常高的片上存储器资源,要么需要非常低的延迟、快速随机存取外部存储器阵列以及高性能存储器访问控制器。由于数据以列为单位,分行读取,读取和写入访问不能都是顺序的,因此很难满足传统缓存和DDR内存芯片的低延迟要求。
雷达处理要求可能相当高。接收器需要连续、实时地处理输入数据。幸运的是,其中大部分都可以使用并行处理结构来实现。波束成形就是一个例子。AESA天线中可能有数百甚至数千个单独的接收/发送单元。天线可以在多个方向上跟踪目标,需要对每个方向进行单独处理。处理必须在两个维度上执行,包括时间(脉冲压缩)和频率(多普勒)。此外,在本雷达基础系列的第#4部分中,如何在空时自适应处理(STAP)中添加额外的处理维度,即空间,这将导致数字信号处理要求的进一步急剧增加。
数值精度问题
雷达系统的设计非常具有挑战性,部分原因是所涉及的信号的动态范围。回到雷达距离方程,接收器处的信号电平与到目标距离的四次方成正比。雷达接收器所需的灵敏度水平远比任何无线通信系统都苛刻。同时,雷达接收机必须应对由于杂波、干扰、干扰、近距离目标甚至发射器本身而可能非常高的接收信号电平。
这需要高数值保真度的数字信号处理技术。为了在潜在的极低信号电平和高干扰水平下实现适当的系统性能,数字处理期间引入的量化噪声电平必须远低于接收器本底噪声。并且,大的不需要的信号必须与非常小的期望接收信号同时表示。这意味着必须保持数据路径的高精度和高动态范围。
定点精度和动态范围由位宽定义。动态范围是位数的 6 倍。例如,16 位宽度提供 96 dB 的动态范围。这听起来可能很多,但信号必须具有保护位以确保没有溢出,并且小信号可能比干扰信号低 100 dB 或更高。为了进行合理的检测,所需信号在到达检测处理时需要高于干扰和噪声30 dB或更高。保持足够的信噪比可能很困难。在处理的每个阶段之后,都需要调整信号电平以保持在定点位宽内。此外,考虑FFT算法。在时域和频域之间转换的过程中,所需的位宽会增加,对于2 n大小的数据长度,通常为n位。
大多数以16位字长工作的处理器和数字信号处理器(DSP)不足以满足雷达处理的许多方面。另一种选择是使用浮点处理器。对于单精度浮点数,24位尾数(包括符号位)可提供144 dB。浮点指数(8 位)允许这个 144 dB 范围在每次操作时自动调整或“浮动”到信号电平,从而提供巨大的动态范围。然而,雷达系统中常见的浮点处理器,如ADI公司的Tigersharc或飞思卡尔的PowerPC,处理能力有限。较新的处理器体系结构提供更高级别的浮点处理能力,主要是通过使用许多内核。权衡是开发环境更加困难,需要复杂的数据流管理,并且消除各种功能之间的数据依赖关系,以便在多个处理器之间进行分区而不会停滞不前。在这些架构中,功耗也可能是一个挑战。
现场可编程门阵列
现场可编程门阵列 (FPGA) 提供了一种替代数字信号处理平台。通常,FPGA用于前端雷达处理,例如波束成形和脉冲压缩。对于高吞吐量,FPGA 的并行结构比处理器具有巨大的优势。十多年前,FPGA 行业对 18 位 DSP 结构进行了标准化。这是对大多数处理器架构提供的 16 位定点精度的改进。
FPGA 供应商赛灵思后来采用 DSP18E 架构(因其 25 位累加器而得名)对 48×48 尺寸乘法器进行了标准化。这是为了更好地支持FFT,如上所述,位增长发生在数据路径中。抖动因子或系数保持在 18 位,而 18 位数据可以再增长 7 位,达到 25 位。FPGA供应商Altera以18×36乘法模式进行反击。最新的创新发生在Altera的28nm Stratix V FPGA上,它提供了一种新的可变精度DSP架构。此体系结构本机支持 18×18、18×36 和 27×27 精密乘法器,均具有 64 位累加器。它支持FIR滤波器、相关器、累加器和FFT的更高精度定点处理,还包括专为定点FFT设计的高效18×25复乘法模式。18×25 复数模式只需三个乘法器,而不是通常需要的四个乘法器,方法是利用内置的前加器和后加器。
FPGA最近的另一项创新是高性能浮点支持,使FPGA并行硬件架构优势能够用于需要浮点动态范围的应用,例如雷达处理。现在可从Altera获得,使用可变精度DSP硬件架构和称为“融合数据路径”的新浮点工具流。
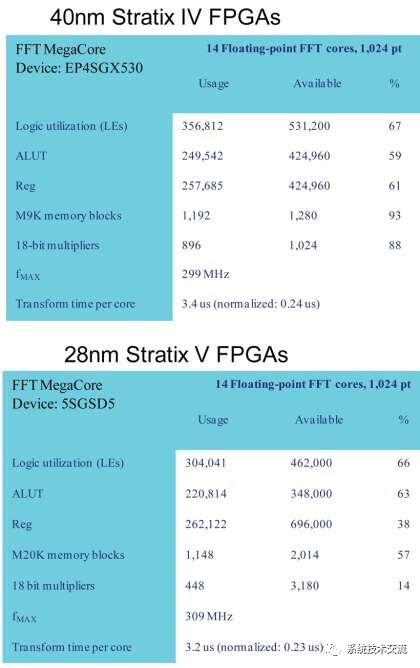
表 2 显示了 1024 个单精度复浮点 FFT(每个 <> 个点)的性能和资源使用情况,这些 FFT 使用 Altera FFT Megacore IP(采用“融合数据路径”技术)构建。本例表明,FPGA现在可以在高密度FPGA中实现大型浮点设计。此外,这是完整的浮点数,而不是“块”浮点数。块浮点对FPGA的完整输入数据集和输出数据集使用通用指数,可以缩放数据样本组,但不能提供高动态范围。这是因为非常小的数据值必须使用最大数据值的指数,这意味着它们无法正确表示。块浮点会导致许多与定点相同的数值问题。
结论
研究时空自适应处理 (STAP) 雷达处理。这类算法提供了超越多普勒雷达处理的能力,但处理要求极高,对浮点的动态范围也有要求。
直到最近,由于这些极端的处理要求,只有最先进的计算机类型才能实现这种类型的算法。然而,现在FPGA可以提供所需的性能水平的复杂浮点处理。如将要显示的,STAP需要处理能力,以便在一毫秒内反转包含100,000个或更多元素的矩阵。
编辑:黄飞
 电子发烧友App
电子发烧友App















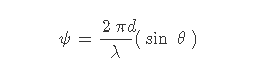











评论