今天我们一起学习一份来自Analog的射频设计笔记。这份应用笔记介绍了射频(RF)和微波子系统组件的系统级表征和建模技术,说明了它们在混合信号、混合模式系统级仿真中的应用。通过使用具有数字预失真 (DPD) 的 RF 发射器作为示例系统,并介绍了这个复杂系统的详细信息和性能数据。
笔记全文如下:
射频 (RF) 和微波世界在很大程度上不受摩尔定律的严格约束,而数字世界中的积极扩展几十年来一直是常态。但现在,由于CMOS晶体管具有数十到数百GHz的皮秒开关速度和转换频率,因此有机会在单个集成电路上将射频和微波组件集成到一个完整的系统中。用于无线局域网和家庭基站的单芯片收发器已经成为商业现实。与复杂的数字系统一样,对一次通过设计成功的需求要求为整个系统的子系统组件提供准确的预测模型,从而能够在将设计提交到硬件之前对系统设计进行仿真并纠正任何错误或故障。这将节省时间和不必要地制造和测试整个系统的成本。
近年来,射频和微波设计的系统级建模和仿真变得非常复杂。AWR 和 Agilent 等 EDA 供应商现已提供具有广泛信号源、组件模型和数据分析工具库的商业仿真工具。射频和微波组件(如放大器和混频器)的非线性行为模型的开发,以及在典型应用环境中准确测量这些子系统的能力,是最近这些模拟器进步的重要推动因素。
本教程介绍了射频和微波子系统组件的系统级表征和建模技术,并说明了它们在混合信号、混合模式系统级仿真中的应用。我将使用具有数字预失真(DPD)的RF发射器作为示例系统,如图1所示。这是一个复杂的系统,包括:
射频组件,例如功率放大器 (PA),为此我们需要一个非线性动力学模型
混合信号元件,如数据转换器和 IQ 调制器/解调器
预失真器的数字组件,可以实现为现场可编程门阵列 (FPGA) 或定制 IC,而这些组件又可以通过高级描述语言(如 Verilog)的模型进行描述,或者通过使用数学语言(如 Mathworks 的 MATLAB 软件)的算法函数来描述。
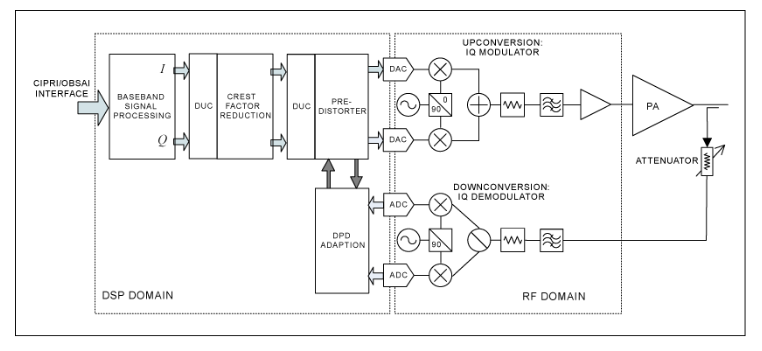
图 1.具有DPD功能的无线基础设施发射机系统的框图和DPD接收机的观察路径。该图显示了我们将要考虑的主要模块和仿真域
具有数字预失真 (DPD) 的射频发射器是实用复杂系统的一个很好的例子。通常,在这样的系统中,独立的团队将设计子系统组件,但重要的是要知道这些组件将作为一个完整的系统协同工作,最好是在硬件用螺栓连接在一起之前。这将使我们能够在设计阶段进行任何必要的架构更改,而不是在硬件构建之后。
我们需要一个能够控制多个不同模拟器引擎并处理它们之间的数据传输的仿真环境。例如,我们可以对系统的射频组件使用谐波平衡或包络瞬态仿真,而系统的数字部分将以时间步长或时间行进的方式进行仿真。我们可能还必须在不同的模拟器中管理浮点和定点数据表示。拥有一个可以管理这种协同仿真的模拟器工具是必不可少的。
在详细介绍模型、模型结构及其在仿真工具中的使用之前,我们先简要回顾一下在此类支持 DPD 的射频发射器系统中遇到的一些设计挑战和注意事项。虽然设计高功率射频放大器以满足宽带CDMA(WCDMA)和长期演进(LTE)等现代频谱高效数字调制通信信号的功率和效率要求已经足够具有挑战性,但DPD的加入带来了一两个额外的皱纹。
WCDMA 和 LTE 等现代数字调制无线通信信号旨在最大限度地提高在给定带宽内可以传输的数据量。现代无线通信数字调制的细节可以在[3]中找到。除了调制和编码方案的复杂性外,这些信号最明显的特征之一是它们具有非常高的峰均功率比(PAPR),在实际情况下介于6dB至10dB之间。换句话说,信号峰值的功率可能比我们想要传输的信号的平均功率高 10 倍。平均功率决定了传输的范围;峰值功率决定了功率放大器的“尺寸”。这意味着放大器必须具有基站覆盖区域所需功率能力的 4 到 10 倍,才能处理峰值。从其峰值容量“后退”运行 AB 类 PA 通常意味着以非常低的效率运行,这是不可接受的,因为运行它的电力成本很高。相反,我们发现像Doherty这样的高效PA架构被用于无线基础设施基站PA。虽然效率很高,但这些功率放大器在以必要的高功率运行时会产生高水平的失真。因此需要某种形式的线性化技术,而DPD是目前的首选方法。
使用 DPD 会带来挑战。首先,我们需要在发射机中建立一条观察路径(见图1),以检测PA产生的失真。预失真器将PA输出与所需信号进行比较,然后使用非线性函数在PA输入信号中产生失真,使PA的输出成为所需信号的复制品。该非线性函数的参数不断调整,以最小化输入信号和PA输出之间的差异。这是一个控制系统。预失真器抵消了PA增益的压缩特性,因此它是一个扩展函数。在频域中,我们看到互调和邻道泄漏功率由DPD补偿。我们可以将其视为预失真器在PA输入中添加频率分量以抵消这些失真产物。有关DPD如何操作的更多详细信息,请参阅[4]。
将DPD添加到发射器的结果是,预失真信号的带宽比原始数据带宽宽得多;宽度最多五倍是常见的准则。这意味着从DPD算法到DAC和RF部分的发射链必须具有宽带宽。对于载波聚合可产生100MHz信号带宽的LTE而言,这是一个重大的设计和实现挑战。观测路径也应具有此带宽,以便能够捕获PA为DPD系统产生的高阶失真产物。此外,观察路径需要比发射机的其余部分更线性,因为就DPD而言,这里引入的任何失真都与PA产生的失真无法区分,并且由此产生的校正信号实际上会在PA输出中引入失真。观察路径需要低噪声和高动态范围,以便能够辨别低电平失真产物。这些都是重大的设计挑战,并增加了变送器的复杂性和成本。
射频行为模型
在过去的二十年中,关于开发非线性射频和微波元件的行为模型已经取得了相当多的工作[5,6]。最近的重点特别放在PA建模上,因为该器件是典型发射机系统中非线性的主要来源。在此期间,识别所谓的“记忆效应”已成为发射机系统建模中最重要的挑战之一。例如,虽然使用多项式模型可以相当直接地对非线性进行建模,但包含记忆效应会使我们的建模和仿真任务变得非常复杂。
射频行为建模有两种主要方法:频域和时域。我们将概述这两种风格。非线性模型通常基于被测系统围绕某个工作点(例如直流条件或平均射频功率)的线性化。任何更通用的东西都太复杂了,无法构建和实现,并且不会简化我们的建模挑战。
频域模型
频域是射频和微波工程师的天然家园。自 Kurokawa 的原始论文 [7] 以及 1960 年代引入矢量网络分析仪以来,我们一直在使用 S 参数进行线性设计近 50 年。因此,这种方法很受欢迎。
X参数模型[8]及其相关和相似的模型结构S函数[9]和“Cardiff”模型[10]是目前流行的现代频域模型。这些模型都基于围绕单个大音调(例如,PA的大信号驱动)的非线性响应的线性化。然后,通过测量对大音调外施加的小谐波信号的散射响应,在频域中探测非线性行为。Verspecht 和 Root 在本杂志 [11] 中清楚地解释了基本原理和数学基础。X 参数模型仅使用一阶导数来模拟非线性行为。这是一种相当优雅的方法,因为一阶导数是由雅可比算法中的模拟器自动计算的,它用于收敛到解,因此该模型简单快捷。S 函数以类似的方式运行,但也可以将 DC 条件作为显式建模变量包括在内。Cardiff 模型通过在模型中包含高阶导数来扩展 X 参数,这与泰勒级数一样,扩展了模型的有效区域并使其更具通用性。
X 参数的价值不仅在于模型公式,还在于构建它们的数据可以使用现成的设备进行测量,例如 AgilentPNA-X 非线性矢量网络分析仪。该仪器还可以构建与 Agilent ADS 模拟器兼容的 X 参数模型文件。在PNA-X周围设置外部测量系统时,高功率PA确实需要格外小心,但这可以扩展仪器测量输出功率超过100W的PA上的X参数的能力[12]。我们还可以从仿真中生成电路的 X 参数描述。这意味着我们可以以相当直接的方式创建电路或子系统的非线性模型,甚至在设计过程的早期,用于更高级别的系统仿真。
X参数方法的一个缺点是这些模型在构造上是无记忆的,尽管最近有关于如何使用基于非线性积分模型的Volterra级数方法将长期和短期记忆效应纳入X参数模型结构的报道[13]。可以使用脉冲技术来测量记忆效应,以观察瞬态行为,并使用 [5],第 3 章中描述的 NIM 方法提取记忆模型参数。内存组件通过乘积项包含在 X 参数公式中。由于长期记忆效应通常是偏置电源元件和PA夹具中偏置线设计的结果,这表明可以将这些电路效应建模为一个单独的模型元件,该元件可以“添加”到晶体管的X参数模型中,以产生完整的PA模型。
时域模型
非线性动力学现象的自然归宿是时域,因为我们可以捕获瞬态,从而捕获能量存储或记忆效应,以及稳态行为。在射频和微波电路中使用时域数据的一个重大历史缺点是,测量的采样率必须非常高,导致采样不足或时间跨度较短的数据集。仿真中也出现了类似的问题:瞬态仿真的时间步长必须非常短,导致仿真时间很长。如今,这些问题已基本得到解决。最近,人们发布了带宽超过60GHz的实时采样示波器,能够使用高达50Gbps的信号进行表征[14]。包络瞬态仿真技术的发展使得在可控的时间内使用调制射频和微波信号对电路进行仿真成为可能。
蜂窝通信中使用的PA通常是相当窄的频带,输出匹配网络滤波器会衰减任何谐波。当这种PA被压缩时,被压缩的是信号的包络,而不是载波信号,它保持正弦波(实际上可能没有明确存在)。这意味着PA的非线性特性可以完全由包络行为来描述。我们可以使用包络,或者更准确地说,使用调制信号来表征PA:数据捕获的时间尺度现在处于调制速率。我们还可以使用包络瞬态仿真来描述调制信号如何受到PA非线性的影响。因此,我们的PA时域模型可以在调制速率下构建,而不是在微波频率下构建。
现代蜂窝通信中使用的数字调制通常以同相 (I) 和正交 (Q) 分量的形式创建。将 I 和 Q 组合在一起以产生所需的调制信号,通常是某种形式的正交相移密钥 (QPSK) 或幅度调制 (QAM)。时域 I 和 Q 数据可以在 PA 的输入和输出端进行测量或仿真,并在 AM-to-AM 或增益响应和 AM-to-PM(相位)响应中观察到非线性和存储器行为,如图 2 所示。从这些图中可以看出增益压缩和相位失真的总体趋势,以及响应在某个平均响应周围的“云”形式。正是这种云表明存在记忆效应。如果不存在记忆效应,这两个响应将是单行的,即“瞬时”响应。云层告诉我们的是,给定输出功率下的增益不仅取决于该时刻的输入功率,还取决于信号在前一个时间的值:它的历史。并非云中的每个点都具有完全相同的历史记录。
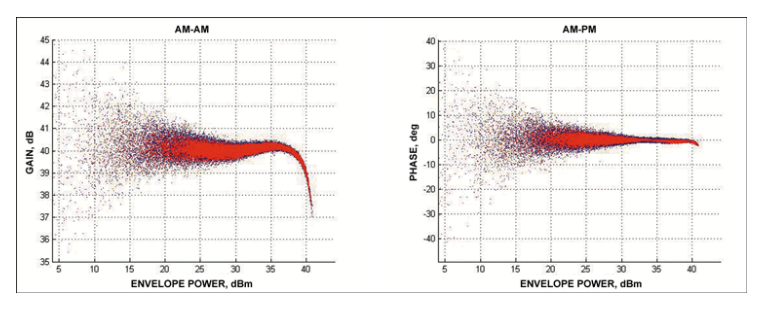
图2.功率放大器输入输出IQ数据的幅度和相位的AM至AM和AM至PM图。蓝点是测量数据,红点是简化的 Volterra 模型预测。
我们可以使用众所周知的非线性数据或函数拟合技术,通过AM-to-AM和AM-to-PM特性拟合曲线来构建PA模型。从本质上讲,我们试图将已知函数拟合到数据中。也许最流行和最简单的技术是多项式拟合数据。在实践中,这通常使用“最小二乘法”来完成,这种方法可以最小化函数和数据之间的平均欧几里得距离。通过构建多项式模型,我们基本上将泰勒级数展开拟合到数据中。
但这个过程会产生一个瞬时模型,无法捕捉到记忆效应。我们需要一个模型函数,在其公式中明确包含时域信号的历史。Volterra 系列来救援。Volterra 系列可用于模拟时不变非线性动力系统;换句话说,一个具有内存的非线性系统。Volterra 级数可以被认为是具有记忆的泰勒级数,附录 B 中提供了简要概述:Volterra 级数作为泰勒级数的发展。由于Volterra级数与Taylor级数相关,两者都是多项式函数,因此Volterra级数也存在类似的局限性[15]。首先,系统中的非线性不能是“强”的。在PA建模的背景下,“强”非线性是指输入信号响应的不连续性,例如由波形削波引起。人们经常说,(PA)系统必须是弱非线性的,才能适应Volterra分析:这意味着系统响应必须是连续的,因此可以用一系列有限的贡献项来表示。有时,“弱非线性”被解释为少量的项——不超过三次!——但这是不必要的人为和限制性的。
通过增加多项式级数中的项数,可以提高 Volterra 级数的精度。换言之,该模型将实际数据近似到更小的容差。虽然增加泰勒级数中的项数是一个简单的练习,但在 Volterra 级数中,交叉项和记忆项会导致序列中的项数随着多项式次数和记忆深度的增加而急剧增加。这也许是 Volterra 系列建模历来应用有限的原因之一。随着现代笔记本电脑现在可用的计算能力,对 Volterra 级数多项式的这种限制已成为过去。
此外,可以使用复杂的“剪枝”技术将多项式中的系数数量限制在可管理的水平,而不会显着损失模型保真度。这种技术是由Filicori、Ngoya及其同事[16,17]开创的,使用了一种称为动态偏差的技术。在这种方法中,Volterra 系列在信号与某个工作点的偏差中显式扩展,无论是直流条件 [16] 还是 PA 的平均信号功率 [17]。在动态偏差中将结果级数截断到一阶,结果令人满意。不幸的是,以这种方式重写 Volterra 级数意味着无法再使用用于识别多项式系数的标准最小二乘技术,因此模型参数难以提取。通过重铸动态偏差表达式,Zhu 恢复了 Volterra 系列的线性参数结构,从而可以通过标准数学技术进行直接的参数提取。这种方法还允许对模型中使用的动力学水平进行显式控制[18]。这种技术被称为动态偏差减少,它可以生成系数相对较少的精确功率放大器模型,通常大约 30 到 50 就足够了。
功率放大器模型
功率放大器通常是发射机非线性的最大贡献者,如今数字预失真所需的宽带宽上与其频率响应相关的存储效应需要复杂的非线性模型来足够准确地描述DPD的PA行为。通常,使用基于多项式(Volterra)的方法,尽管市场上也有明显的例外。用于窄带信号的简单存储多项式模型已被简化的 Volterra 系列模型所取代,这些模型包括该系列的存储项(交叉项)之间的一些交叉耦合。这些模型通常基于解调的IQ数据构建,因此是RF PA的基带模型。它们通常在 MATLAB 等环境中构建为数学模型。PA和行为模型的AM-to-AM和AM-TO-PM特性如图2所示。这些是输出 IQ 的幅度和相位与输入 IQ 时域数据的关系图。这样的模型可以很容易地用于系统仿真。
DPD 系统建模
预失真函数是一种非线性函数,用于补偿PA增益压缩、相位转移特性和记忆效应,从而产生PA的线性输出。如上所述,此应用中经常使用基于 Volterra 的函数。
用于求解 Volterra 模型的 DPD 算法通常使用 MATLAB 等数学语言开发,它提供了一组丰富的工具和函数,用于求解非线性方程、优化函数系数等。自适应线性化常用的两种DPD方法是直接自适应和间接学习,如图3所示。直接适应是一种经典的控制方法;它直接比较输入信号和(缩放的)PA输出信号,并使用误差来驱动DPD函数参数的变化,以最小化下一次计算的误差。间接学习是一个稍微复杂的数学过程,但似乎更容易实现。在这里,我们将预失真的输入信号与后失真的PA输出进行比较;我们使用相同的非线性预失真函数。Volterra 系列在数学上已经证明,在一定范围内,前失真和后失真会产生相同的行为。同样,我们使用误差来驱动预失真函数参数的变化。这似乎更容易实现,因为DPD函数参数用于计算用于误差(成本)函数的两个信号,并且更新的参数是最小化例程的直接结果。
用于估计新的DPD函数系数集的自适应例程通常是最小二乘求解器。如前所述,由于用于 DPD 的非线性 Volterra 模型被设置为参数线性表达式,因此可以使用最小二乘法。通常使用最小均方 (LMS) 等最小二乘最小化例程,并采集数千个数据 (IQ) 样本来求解这组过度确定的方程。LMS 例程通常非常稳定,但收敛速度可能很慢。已经证明了更激进的最小化技术,如递归最小二乘法(RLS)和仿射投影(AP)[19],提供了更快的收敛,尽管它们更容易因输入数据中的噪声而产生不稳定。这可以在实施中克服。
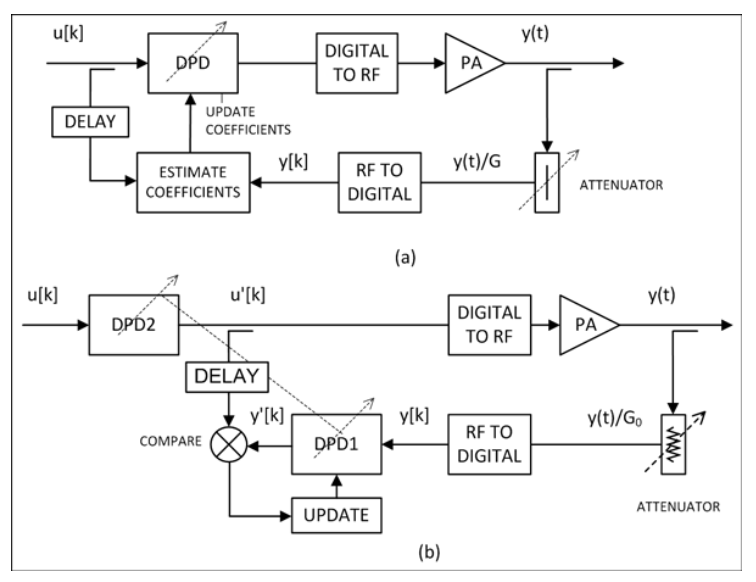
图3.DPD函数的示意图表示:(a)是自适应控制,(b)是间接学习。
在MATLAB环境中演示DPD算法后,可以将DPD模型导入系统仿真器,并在更复杂的多仿真器环境中仿真PA的线性化。验证系统性能后,可以使用 Xilinx 和 Altera 等 FPGA 制造商提供的开发软件将 MATLAB 模型代码直接下载到 FPGA 中。然后,数学模型可以在硬件中实时运行,并且可以快速解决任何实际实现错误。
混合信号模型和仿真
现在,我们只需要对将数字器件(预失真器)连接到射频功率放大器的“胶水”电路进行建模和仿真。通常,系统规格中省略了这些电路和组件,线性化性能的验证仅集中在PA和DPD模型上。但实际上,这些组件的作用不仅仅是胶水。如前所述,DPD观测路径是这种线性化发射机系统的关键组成部分,其性能会对发射机的整体运行和能力产生重大影响。
通过数据转换器、调制器和解调器(调制/解调)以及射频组件(如驱动器和低噪声放大器)的合适模型,我们可以详细仿真整个发射器的行为。我们可以使用仿真来研究这些组件的规格对线性化发射机整体性能的影响。例如,我们可以研究调制/解调电路中本振的相位噪声性能对观测路径精度和动态范围的影响,从而测试整个系统的线性化能力极限。我们为这些组件和电路选择的模型将在很大程度上取决于我们希望仿真行为的复杂程度,以及损伤对线性化的重要性。
数据转换器
数模转换器 (DAC) 和模数转换器 (ADC) 的模型范围从简单的输入/输出模型到功能行为的 Verilog 描述,再到接近(甚至超过)PA 非线性模型复杂性的复杂非线性模型。数据转换器是非线性器件。在较高层次上,非线性可以建模为频域中的谐波产生。更复杂的模型将使用多项式或 Volterra 方法。在发射器的系统级描述中,包括一个简单的非线性和噪声系数就足够了,特别是对于观察路径中的ADC,以模拟和研究低失真信号功率对线性化能力的限制。
安捷伦的 SystemVue 和 AWR 的虚拟系统仿真器 (VSS) 等系统级仿真工具为许多商用数据转换器提供了内置模型。虽然这对于验证最终系统很有用,但使用这些工具中提供的更通用的数据转换器模型,我们可以研究这些组件的一些更直接的局限性,例如数据位数、噪声系数、时钟频率和频率响应等。这些研究可以让我们更好地了解这些因素的局限性或对整体系统性能的损害的性质。
IQ调制器/解调器电路
在我们的仿真中,我们可以使用理想的IQ调制和解调函数模型,或者模拟电路描述或宏模型,其中包括许多影响这些器件性能和性能限制的物理行为。我们主要关注的可能是这些对理想解调器行为的损害对观测路径性能的影响。这种损伤包括从本振(LO)注入噪声,因此LO相位噪声性能值得关注,以及解调器中I和Q路径之间的串扰。
这些IQ解调器缺陷可以使用Cavers[20]描述的简单分析电路模型进行建模,如图4所示。理想解调器的输出通常作为RF或系统级仿真器中的内置模型提供,通过两个线性放大器馈送,从而可以对增益不平衡进行建模。相位不平衡 Φ 或 I 和 Q 路径之间的正交相位差分别使用正弦 (Φ) 和余弦 (Φ) 中的串扰放大器和直插放大器进行建模。该分析模型的输出允许将直流偏移包含在调制器的输出中。这对于零中频下变频架构非常重要。
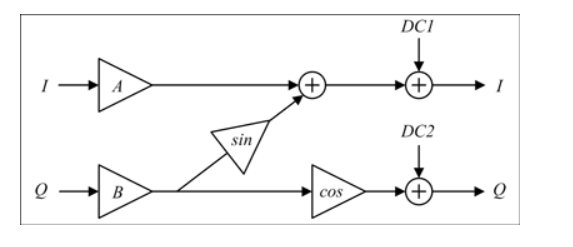
图4.IQ解调器损伤的分析电路模型。
RF放大器和滤波器
发射路径中的PA驱动放大器通常不会被驱动得太用力,因此它们的非线性行为比PA本身更受关注。这意味着我们可以为这些组件使用更简单的行为模型,也可以使用组件供应商提供的用于射频电路仿真器的非线性模型。但是,在使用这些模型之前,应检查它们是否可以用于瞬态仿真,因为系统仿真将使用时间步长(瞬态)算法。驱动放大器的非线性产生的任何失真都将包含在PA的净输出中,并且实际上将由预失真器容纳。在系统级仿真中,我们主要关注的是这些非线性能否得到充分的捕获,并描述它们对发射机整体非线性行为的影响。如上所述,非线性行为的主要来源是PA本身。因此,正确描述PA的非线性动力学行为是最重要的。
观察路径中的低噪声放大器(LNA)在确定预失真系统的噪声水平或灵敏度方面起着重要作用。同样,通常只需使用系统或RF仿真器中可用的系统级模型,并调整该组件的增益、噪声系数和频率响应,即可了解并最终控制这些性能规格对线性化系统整体性能的贡献。
发射和观察路径还将包含滤波器和衰减器等无源元件,用于控制系统主要部件(PA驱动器和LNA)输入端的频率响应和信号电平。我们可以直接在系统模拟器中使用这些组件的 S 参数描述,前提是没有太多的色散。S 参数模型将进行卷积以生成时域描述。
把它们放在一起
现在,我们在各种仿真工具中拥有一组模型,可以最佳地描述发射机系统的组件。然后,我们通常会求助于商业系统级仿真工具,例如安捷伦的 SystemVue 和 AWR VSS,以提供框架和一些模型,以将系统描述放在一起并管理仿真。我在这里使用了“管理”这个词;它给人一种模拟如何进行的良好感觉。系统模拟器通常是一个时间步长模拟器,因此我们观察数据逐步通过我们的系统进行。因为并非所有我们想要使用的模型都以这种方式工作,或者可能不会用系统模拟器的本地语言进行描述,所以提供了“协同仿真”。
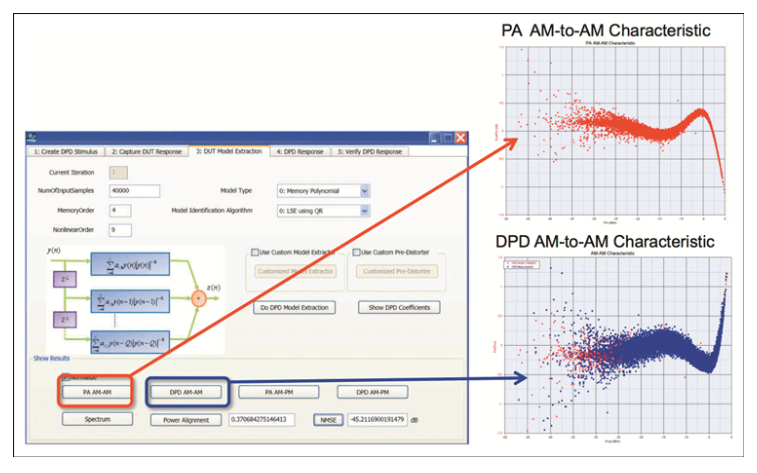
图5.Agilent SystemVue 软件 DPD 示例项目的屏幕截图,表明如何根据 PA AM-to-AM 特性构建存储器多项式 DPD 算法。
通过协同仿真,我们的意思是主机系统仿真器将启动并控制另一个仿真器引擎,例如MATLAB或ADS谐波平衡或电路包络;它将执行 PA 模型或 DPD 算法的仿真,以获取系统仿真中下一个时间步的适当数据。以这种方式描述,听起来系统仿真需要花费大量时间。但事实并非如此。秘诀在于如何有效地管理协同仿真,以及如何在正确的时间传输相关数据。与电路仿真相比,系统仿真速度非常快,因为我们可以将主要的非线性“捆绑”到几个组件中,而在具有多个晶体管的电路仿真中,包含多个非线性模型的仿真的收敛可能会变得很慢。这些其他模拟引擎在“后台”运行,无需用户进行任何显式控制。
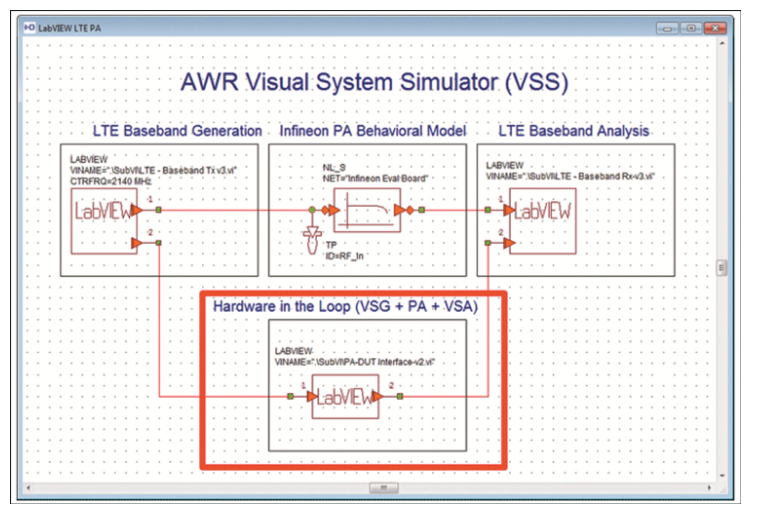
图6.AWR VSS 的屏幕截图显示了如何使用 National Instruments Labview 工具将 PA 的 实时 测量 数据 导入 到 系统 仿真 中
如果我们没有我们需要的模型怎么办?这不是不进行系统仿真和验证设计的正当借口。例如,我们可以将测量数据(例如从PA中)直接导入到系统仿真中,并了解整个系统将如何工作。如图6所示,以NI LabVIEW工具和AWR VSS为例。这是检查系统如何组合在一起的非常有用的方法;它允许对系统的不同部分进行更改,以适应真实的测量效果。如果您正在开发一个 DPD 系统,该系统应该足够通用,可以与多个不同的目标 PA 一起使用,则可能会出现这种情况,通常情况就是这样。PA的模型并不总是可用或准确的,协同仿真和表征提供了一条前进的道路。
结束语
在本教程中,我们只了解了如何使用来自不同来源的模型和测量来组合系统仿真。这些模型可以组合在一起,系统仿真器可以快速有效地管理模型在其原生环境中的协同仿真。我们已经描述了如何构建其中一些模型,并通过研究系统中关键组件对理想性能的损害,在系统级别用于研究如何设置规格。
附录 A:记忆效应
“记忆效应”是用于描述信号历史对其现值的影响的术语。换言之,过去时间实例的信号值对当前值有贡献。对于电气工程师来说,这种行为应该不足为奇:一个简单的串联 R-C 电路表现出记忆效应,因为电路中流动的电流取决于电容器上已经积聚了多少电荷。记忆效应是系统中能量储存的结果。它们也是系统动力学行为的一种表现形式,对于线性系统,可以用时间导数或时间延迟表达式来描述。对于功率放大器等非线性系统,信号的历史会影响输出。PA中的动态效应可以在很宽的时间尺度上发生。
“短期”记忆效应大致以射频载波速率发生。短期记忆的贡献者包括放大器中与频率相关的匹配网络,以及晶体管本身的内部电容和电荷传输时间。如果这些电容也是非线性的,例如作为电源电压的函数,那么记忆效应也是非线性的。
“长期”记忆效应的发生速度要慢得多,并且可以在一段时间内影响PA的行为。长期记忆效应的例子包括通过去耦电容和印刷线电感在PA的偏置和供电线路中存储能量,以及由调制信号驱动下晶体管的加热和冷却引起的温度变化;半导体的热时间常数比调制频率长得多。
附录 B:Volterra 级数作为泰勒级数的发展
建立 Volterra 级数表达式的一种方法是开发非线性瞬时模型,该模型可以用泰勒级数展开来描述。我们以一个多项式模型为原型来描述一个非线性瞬时系统:
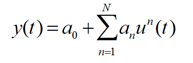
多项式系数 an从泰勒级数中发现的输入输出关系,围绕某个操作点展开,u0:
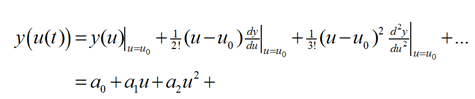
现在,让我们将输出 y(t) 视为 u(t) 和 u 在之前某个时间的值的函数,而不是瞬时关系,从而描述记忆效应:
y(t) = ƒ(u, u1、u2, ..., un)
哪里
u = u(t), u1= u(t - τ1)、u2= u(t - τ2), ...
对此的泰勒级数展开是:
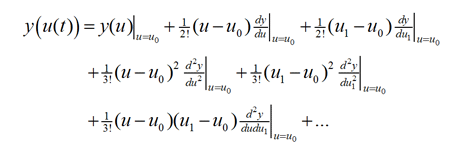
这是一个多项式级数。(u 中的内存项1、T0)和所谓的Volterra交叉项(u - u0(u1、T0)可以很容易地在这个表达式中观察到。
Volterra 级数可以被认为是具有记忆力的泰勒级数。这种级数所描述的非线性必须满足一些“平滑度”标准,才能使级数收敛。这是另一种说法,即序列将函数的真实值近似到某个指定的容差范围内,即截断误差变得小于该容差值。
References
Agilent EDA: 'SystemVue,' at www.agilent.com/find/eesof-systemvue.
Applied Wave Research: 'Virtual System Simulator,' at https://www.awr.com/software/products/visual-system-simulator.
McCune, E. Practical Digital Wireless Signals, Cambridge University Press, 2010.
Wood, J. Behavioural Modeling and Linearization of RF Power Amplifiers, Artech House (in press).
Wood, J. and Root, D. E., eds. Fundamentals of Nonlinear Behavioral Modeling for RF and Microwave Design, Artech House, 2005.
Pedro, J. C. and Maas, S. A. "A comparative overview of microwave and wireless power-amplifier behavioral modeling approaches," IEEE Trans. Microwave Theory and Techniques, vol 53(4), pp 1150-63 (2005).
Kurokawa, K. "Power waves and the scattering matrix," IEEE Trans. Microwave Theory and Techniques, vol 13(2), pp 194-202 (1965).
Root, D. E., Verspecht, J., Sharrit D., Wood, J., and Cognata, A. "Broad-Band Poly-Harmonic Distortion (PHD) Behavioral Models From Fast Automated Simulations and Large-Signal Vectorial Network Measurements," IEEE Trans. Microwave Theory and Techniques, vol 53(11), pp (2005).
Verbeyst, F. and Vanden Bossche, M. "Measurement-based Behavioral Model under Mismatched Conditions," 35th European Microwave Conf, 5 October 2005.
Woodington, S., Williams, T., Qi, H., Williams, D., Pattison, L., Patterson, A., Lees, J., Benedikt, J., Tasker, P. J. "A novel measurement based method enabling rapid extraction of a RF waveform look-up table based behavioural model," IEEE MTT-S International Microwave Symposium Digest, 15-20 June 2008, (2008) 1453-1456.
Verspecht, J., Root, D. E. "Polyharmonic Distortion Modeling," IEEE Microwave Magazine, vol 7(3), pp 44-57, (June 2006).
Wood, J., Collins G. "Investigation of X-parameters measurements on a 100 W Doherty power amplifier," 75th ARFTG Conference Proceedings, Anaheim, CA, 28 (May 2010).
Soury, A., Ngoya, E. "Handling long-term memory effects in X-parameter model," IEEE MTT-S International Microwave Symposium Digest, 18-23 June 2012.
Agilent Infiniium 90000-Q series, at www.agilent.com/find/90000QSeries.
Aaen, P., Pla, J., Wood, J. Modeling and Characterization of RF and microwave power FETs, Cambridge University Press, 2007.
Filicori, F., Vannini, G., Monaco, V. A. "Nonlinear Integral Model of electron devices for HB circuit analysis," IEEE Trans. Microwave Theory and Techniques, vol 40(7), pp 1456-64 (1992).
Soury, A., Ngoya, E., Nebus, J. M., Reveyrand, T. "Measurement based modeling of power amplifiers for reliable design of modern communications systems," IEEE MTT-S International Microwave Symposium Digest, June 2003, pp 795-798 (2003).
Zhu, A., Pedro, J. C., Brazil, T. J. "Dynamic deviation reduction-based Volterra behavioral modeling of RF power amplifiers," IEEE Trans. Microwave Theory and Techniques, vol 54(12), pp 4323-32 (2006).
Zhou, D., DeBrunner, V. E. "Affine projection algorithm based direct adaptations for adaptive nonlinear predistorters," 40th Asilomar Conference on Signals, Systems and Computers ACSSC06, pp144-147 (2006).
Cavers, J. K. "The effect of quadrature modulator and demodulator errors on adaptive digital predistorters for amplifier linearization," IEEE Trans. Vehicular Technology, vol 46(2), pp 456-466 (1997).
审核编辑:黄飞
 电子发烧友App
电子发烧友App
























评论