作者:董名轩,香港中文大学(深圳)理工学院
1 引言
在日常工作和生活中,我们会接触到许多不同类型的单位。比如大家熟知的国际基本单位(International System of Units, SI 单位),共有七个基本量:长度(米,m),质量(千克,kg),时间(秒,s),电流(安培,A),热力学温度(开尔文,K),物质的量(摩尔,mol)和发光强度(坎德拉,cd)。物理学各个领域中的其他的量,都可以由这七个基本量通过乘、除、微分或积分等数学运算导出。此外,还有一些非 SI 单位制的单位,比如在电磁学中十分常见的计量单位,分贝(decibel, dB)。它是度量两个相同单位的数量的比例的计量单位。其中,“分(deci)”表示十分之一,“贝(bel)”则取自于美国发明家亚历山大·格雷厄姆·贝尔(Alexander Graham Bell)。
2 感知的差异
想更好地了解分贝这个单位的起源,我们不得不从感知的差异聊起。
在 19 世纪,不同国家的物理学家和心理学家,都发现一个现象:对于人体的感知来讲,心理量和物理量有一个对应关系,即同一刺激的差别量必须达到一定比例,才能引起感觉的差别。先后对这一现象进行过研究的学者们有:法国物理学家 P·布格尔、赫尔姆霍茨、德国莱比锡大学解剖学教授 E·H·韦伯、莱比锡大学物理学教授古斯塔夫·西奥多·费希纳、美国发明家亚历山大·贝尔等。
韦伯研究发现:“人类产生可查觉的最小刺激的增加的量与初始存在的刺激成正比”,它可以用一个分数来表示,这个分数虽然随着被试的感觉不同而有变化,但对于一定的感觉来说却是不变的。比如用手提起 1 公斤的物体时,人们可能会在重量增加到 1.2 公斤时感受出重量的差异。而当初始重量为 10 公斤时,人们可能需要在重量增加到 12 公斤时才会感受到明显的差异。后来,韦伯的学生费希纳将韦伯的研究结果总结为了数学形式: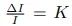 ,这便是人们所熟知的韦伯定律。其中,∆I 代表刺激的差别感觉阈限(Just Noticeable Difference),I 代表标准刺激的强度,K 为一常数(又称韦伯分数或韦伯率)。
,这便是人们所熟知的韦伯定律。其中,∆I 代表刺激的差别感觉阈限(Just Noticeable Difference),I 代表标准刺激的强度,K 为一常数(又称韦伯分数或韦伯率)。
韦伯的学生费希纳在后续进一步的研究中发现,不同人对不同的刺激有不同的敏感度。他认为,主观感觉与刺激强度的对数成正比。比如人对光和声音的感知满足等式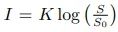 ,其中 I 为主体感受的强度,S 为刺激强度,S0 为刺激的阈值振幅,K 为一常数[12]。它说明心理量是刺激量的对数函数,即当刺激强度以几何级数增加时,感觉的强度以算术级数增加。这被后世称为“费希纳定律”。简单来说,这个定律说明了人的一切感觉,包括视觉、听觉、肤觉(含痛、痒、触、温度)、味觉、嗅觉等,都遵从感觉不是与对应物理量的强度成正比,而是与对应物理量强度的常用对数成正比。
,其中 I 为主体感受的强度,S 为刺激强度,S0 为刺激的阈值振幅,K 为一常数[12]。它说明心理量是刺激量的对数函数,即当刺激强度以几何级数增加时,感觉的强度以算术级数增加。这被后世称为“费希纳定律”。简单来说,这个定律说明了人的一切感觉,包括视觉、听觉、肤觉(含痛、痒、触、温度)、味觉、嗅觉等,都遵从感觉不是与对应物理量的强度成正比,而是与对应物理量强度的常用对数成正比。
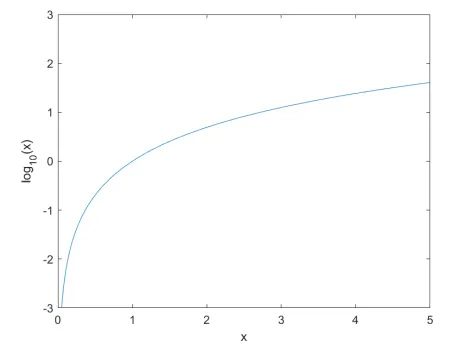
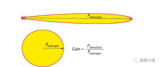
上图是一张标准对数的曲线图,假设 x 为刺激强度,y = log10(x) 为感受强度,切线的斜率变化为单位刺激量变化带来的感受的变化。我们可以看到,人类对持续的、相同强度的刺激的反应会逐渐变得迟钝。这是高速公路不会修建成一条直路的原因,需要不断地设置缓慢的转弯以给司机不同的刺激,降低司机因反应迟钝造成事故的几率。另一方面,这也是人类对自身的保护机制。在刺激量很大时,人体对于稍微改变的刺激反应较小,以保护各种感受器官;而在刺激量较小时,人类对于稍微改变的刺激反应较大,以保护身体的安全。
在这里,我们接触到了 log,即对数运算。为了便于接下来的介绍,我们需要先了解一些对数运算的知识。
3 对数的简单介绍
我们说对数为指数的反函数,并且称 logb a 为“a 以 b 为底的对数”。我们可以计算任意底的对数 L = logb a,它的意思是为了得到数字 a,必须以 b 为底的幂(指数),且 bL = a 等同于(base)logarithm = number[6]。举个例子,25 = 32,则 log232 = 5。我们常用的对数性质有:
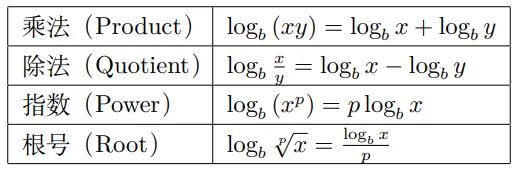
以 10 为底的对数是日常生活中最常用的对数,被称为常用对数,可写为 y = log x,它们的运算很方便,因为 10 的幂很容易计算[9]。除此以外,e 和 2 也是常用的底。
有了这些基础的对数知识,我们马上来讨论分贝。我们将会了解,当使用分贝单位时,能使工程运算,尤其是涉及特别大或特别小的比量时,变得非常简单。
4 分贝
4.1 亚历山大·格雷厄姆·贝尔
我们前面提到过,“bel”取自于亚历山大·格雷厄姆·贝尔的姓氏[10]。贝尔于 1874 年 3 月 3日出生于苏格兰爱丁堡市,1922 年 8 月 2 日逝世于加拿大新斯科舍省。在贝尔下葬那天下午 6:25,美国全国的电话线路停止服务了一分钟,以示纪念[13]。
贝尔最被人所铭记的成就是他发明了电话。然而,他也在许多其它领域做出了非常大的贡献。如:贝尔改进了爱迪生发明的留声机,发明了早期金属探测器,还与凯西·鲍德温一同设计出了当时速度最快的水翼船 HD-1,速度达到了 30 英里每小时。贝尔也非常重视科学技术的发展,他曾是国家地理学会的主席,《国家地理》及《科学》杂志的创始人之一。
此外,贝尔还有一件非常值得称道的是他将自己的一生奉献给了聋哑人的教育事业。他接过并且改进了由他的父亲,亚历山大·梅尔维尔·贝尔开发的可视言语系统,这是一种用于帮助聋人学习以及提高他们语言能力的系统。著名作家海伦·凯勒就曾是贝尔的学生及挚友。也正是在这个过程中,他对人类的听力系统进行了深入的研究。
4.2 分贝的历史及定义
在电话被发明后,自然地,人们需要量化地测量任何电话系统中的声音传输效率[11]。在分贝之前,人们曾使用过两种不同的单位来衡量,自然衰减单位(The Natural Attenuation Unit)和标准电缆英里(Mile of Standard Cable)。自然衰减单位的定义是:
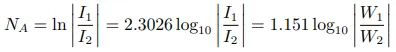
其中 I1 和 I2 流入相同的阻抗,W1 和 W2 是由 I1 和 I2 流入相同的阻抗所产生的功率[10][11]。上式的最后一步用到了在给定系统的一点: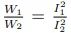 ,及对数的指数性质。然而,由于自然衰减单位的尺寸不方便,人们更常使用另一单位,标准电缆英里[11]。标准电缆的定义为:阻值为 88 欧姆/英里的 19 股开线电缆,电容为 0.054 微法/英里[7]。标准电缆英里的定义为:
,及对数的指数性质。然而,由于自然衰减单位的尺寸不方便,人们更常使用另一单位,标准电缆英里[11]。标准电缆的定义为:阻值为 88 欧姆/英里的 19 股开线电缆,电容为 0.054 微法/英里[7]。标准电缆英里的定义为:
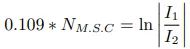
或
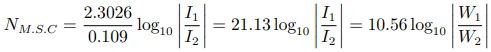
通过与自然衰减单位的对比,我们知道 1 标准电缆英里约等于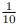 自然衰减单位[11]。这可能会让人有些困惑,我们可以通过一张图片来描述。
自然衰减单位[11]。这可能会让人有些困惑,我们可以通过一张图片来描述。
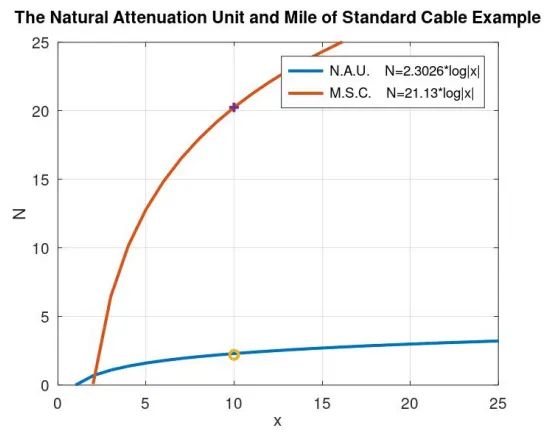
可以看到,当假设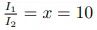 的时候,我们得到了约 2 自然衰减单位和约 20 标准电缆英里。我们也可以说,标准电缆英里相较于自然衰减单位可以反映出更细微的变化。
的时候,我们得到了约 2 自然衰减单位和约 20 标准电缆英里。我们也可以说,标准电缆英里相较于自然衰减单位可以反映出更细微的变化。
由于标准电缆的衰减常数随频率变化而变化,且使用 796.4 周期(ω = 5000)的频率没有得到普遍认可,人们采用了一个新单位,新电话传输单位(New Telephone Transmission Unit),并且 TU 单位有如下优点:(1) 不随频率变化而变化;(2) 尺度合适;(3) 具有简单的物理意义[11]。它的定义为:
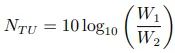
TU 的大小被选择为与 MSC 相近。准确地说,1.0TU=0.947MSC 或 1.0MSC=1.056TU[7]。
而 TU 单位,就是分贝(dB)单位的前身!在 1928 年,贝尔实验室将 TU 重新命名为“decibel”,即分贝。而且与我们在网上看到的消息不同,“贝尔”与“分贝”这两个单位并不是先后被定义的,而是同时定义的。在这篇 TU Becomes Decibel 中,作者 R.V.L. Hartley 指出:因为一个乘方的对数被乘了十以得到 TU 单位,这提示 TU 天然为派生单位,则“贝尔”之名应被授予其基本单位;又因为 TU 的数值为贝尔数值的十倍,则 TU 的大小应为贝尔的十分之一,所以它将成为“分贝”[10]。
4.3 分贝的基本性质
1) 我们为什么使用分贝
简单地讲:使用分贝单位将极大简化我们的计算!您已经了解,分贝其实就是对数运算,它的特点是可以将乘法转换为加法、除法转换为减法以及开根号运算转换为除法。在对数运算被发明的最早期,它的目的就是为了减轻当时科学家们计算的难度。最初的对数以对数表的形式出现,您可以将它理解为原始的计算器。
在这里,我们引入几个便于我们日常理解和运算的分贝数:1dB、3dB 和 10dB。我们说:±1dB对应增加或减少 26% 的增益;+3dB 增益为增加一倍功率,-3dB 为增益降低到原来的一半;+10dB 的增益需要十倍的功率,-10dB 的变化意味着将原始值降低到 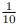 。在声学领域,由于人体对刺激感知的特点,+10dB 的变化在经验中被定义为大多数人认为“两倍音量大小”的值,所以,假如您想要让家中耳机或音响的声音大一倍,您将需要十倍的功率!也就是提升 10dB 的功率。以此类推,如果我们需要输出功率增加 20dB,则需要一百倍的功率!我们通过一个小推导来支持这个结论。以 +3dB 为增加一倍功率为例,假设我们正在计算的某一输出为
。在声学领域,由于人体对刺激感知的特点,+10dB 的变化在经验中被定义为大多数人认为“两倍音量大小”的值,所以,假如您想要让家中耳机或音响的声音大一倍,您将需要十倍的功率!也就是提升 10dB 的功率。以此类推,如果我们需要输出功率增加 20dB,则需要一百倍的功率!我们通过一个小推导来支持这个结论。以 +3dB 为增加一倍功率为例,假设我们正在计算的某一输出为
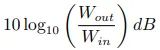
将输出功率增加一倍,我们会得到
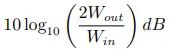
根据对数的乘法性质,上式将等于
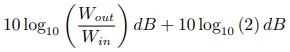
这时,如果将上式第二项输入计算器,我们将会得到 3.01029995664,即大约 3dB。余下的推论将类似。也就是说,假如我们有两个分别为 60dB 的功率放大器,那么它们一起输出时的总功率将会是约 63dB,而不是 120dB。
又假设我们有一串联放大器系统,其增益分别为 10dB,6dB,1dB,总增益为 17dB。假如
我们使用公式计算,根据分贝瓦的公式
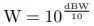
假设输入为 1W 时,我们得到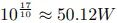 。但是,计算这样的幂指数略显不便。而当我们利用分贝的性质时,只需要将其分成 10dB + 3dB + 3dB + 1dB,对应的放大的倍数为 10倍,2 倍,2 倍和 1.26 倍。代入 1W 的输入,输出约为 1W ∗ 10 ∗ 2 ∗ 2 ∗ 1.26 = 50.4W。可见两者非常的接近。这就是在工程实践中,分贝单位能够带来的便捷性,可以让我们更简单地进行运算。
。但是,计算这样的幂指数略显不便。而当我们利用分贝的性质时,只需要将其分成 10dB + 3dB + 3dB + 1dB,对应的放大的倍数为 10倍,2 倍,2 倍和 1.26 倍。代入 1W 的输入,输出约为 1W ∗ 10 ∗ 2 ∗ 2 ∗ 1.26 = 50.4W。可见两者非常的接近。这就是在工程实践中,分贝单位能够带来的便捷性,可以让我们更简单地进行运算。
2) 分贝的简单估算
在某些时刻,我们可能需要快速地估算某些系统的增益,这时精度相对不那么重要。我们需要记住如下三个等式:
10 log10(2) ≈ 3.01029996
10 log10(3) ≈ 4.77121255
10 log10(5) ≈ 6.98970004
这样,我们就可以进行估算了。例如,设我们有一系统,它的增益为
10 log10(15)dB
则根据对数的乘法运算性质,它也等于
10 log10(3 ∗ 5)dB = 10 log10(3)dB + 10 log10(5)dB
即该系统增益约等于 4.8 + 7.0 = 11.8dB。我们将 10 log10(15) 输入计算器验算,得出的结果约等于 11.76091259。再举一个小例子,假如我们的系统输出为
10 log10(7)dB
这时我们可以将它估算为
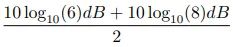
我们计算的结果约为 8.41dB,而 10 log10(7) ≈ 8.45dB。
有了上面三个基本的对数等式,我们可以快速估算出几乎所有系统的分贝输出。
3) 分贝自身是无量纲量
在物理学中,分为有量纲量与无量纲量两种量。一类物理量的大小与度量时所选用的单位有关,称之为有量纲量,例如长度、时间、质量、速度、加速度、力、动能、功等就是常见的有量纲量;另一类物理量的大小与度量时所选用的单位无关,则称之为无量纲量,例如角度、两个长度之比、两个时间之比、两个能量之比等[16]。具体到分贝单位,当它仅作为 dB 时,是一个无量纲量,因为它仅仅是两个功率或电流的比值的对数,与度量时所选的单位无关;而当分贝加入后缀时,例如 dBW,这时它就成为了有量纲量,因为现在它以 1W 作为参考单位。
4.4 常见的分贝单位
分贝也被应用于多种不同的学科与领域,我们在这里简单介绍几种。它们是:
1) dBm 与 dBW
分贝毫瓦与分贝瓦是一种电平单位,用来表示功率电平相对于毫瓦或瓦的分贝。分贝毫瓦的定义为
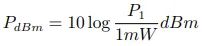
其中 P1 被标准化至 1 毫瓦[15]。我们也可以通过对数的性质推出,若要将任意 dBm 表示为毫瓦,所使用的公式为
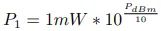
分贝瓦与分贝毫瓦类似,只不过使用 1W 而不是 1mW 作为参考。在电话与音频电路中,0.775V 信号电平施加于 600Ω 的电阻产生 1 毫瓦的功率[3],而在射频电路系统中,电阻的参考值为 50Ω[4]。
2) dBu 与 dBV
dBu 和 dBV 都是专门用于测量电压的分贝单位。其中,dBu 是相对于 0.775V 的 dB 单位;dBV 是相对于 1V 的 dB 单位,于是我们有:0dBu = 0.775V ,0dBV = 1V ,并且 dBu 始终等于 dBV + 2.21[2]。其它与 dBu 和 dBV 有关的公式有[8]:
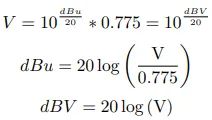
需要注意的是,dBV 的 V 应始终大写,以便于同 dBu 区分。
3) dBi 与 dBd
dBi 或 dB(isotropic) 的定义为天线的增益与理论各向同性天线的增益的比较,理论各向同性天线在所有方向上均匀分布能量;dBd 或 dB(dipole) 的定义则为天线增益与半波偶极子天线增益的比较。dBi 的公式为
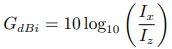
Ix 为定向天线的电磁强度,Iz 为各向同性天线的电磁强度[14]。上式也可表达为
GdBi = 10 log10 (G)
G 为天线的增益因子。然而,我们无法真正制造出理论的各向同性天线,所以人们也将简单且效率极高的半波偶极子天线作为参考对象,即 dBd。由于半波偶极子天线的定向增益为1.64,则它的公式为
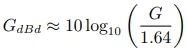
通常来讲,
GdBd ≈ GdBi - 2.15dB
这两种单位都经常被使用,需要注意的是:当指定了天线增益单位为 dBi 或 dBd 时,一般不会产生歧义。而如果仅指定了天线增益单位为 dB,则需要进一步参考资料。
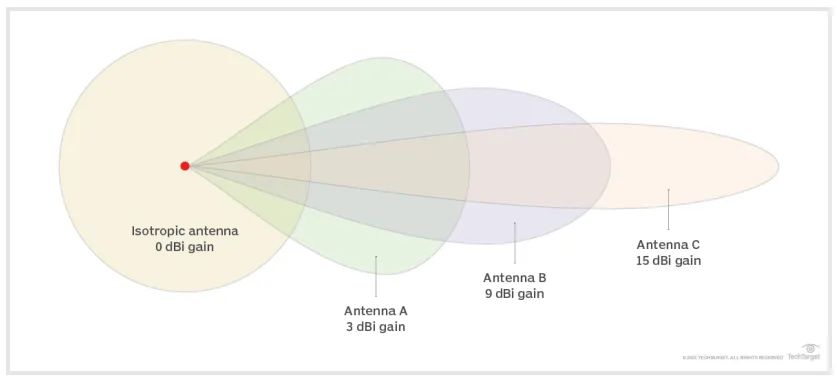
图源:TechTarget
不同的 dBi 增益

图源:Tele-Tech Magazine
飞机高度计的半波偶极子天线
4) dBc
dBc 或 decibel relative to carrier 的定义为信号与载波信号的功率比。如令 Psignal 为某调制信号功率,Pcarrier 为未调制载波信号功率,则瞬时调制信号信号的强度为
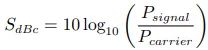
若 SdBc 为正,信号强度大于载波信号强度;反之若 SdBc 为负,则信号强度小于载波信号强度[5]。
5) dBsm
又称 dB (m2),相较于一平方米的分贝单位,常用在雷达散射截面(Radar Cross Section,RCS)测试与天线有效面积的测试中。
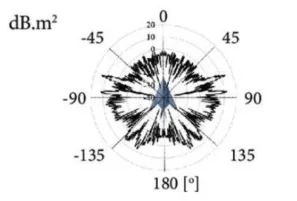
图源:Calculation of Aircraft Target’s Single-Pulse Detection Probability[17]
F-117 的 RCS 测试结果
6) dB SPL
声压级是我们形容声音大小的单位,也是日常最多接触到的分贝单位。例如安静的房间约为30dB、正常说话的声音约为 60dB、飞机起飞时约 140dB。声压级的定义为
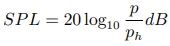
其中 ph 为参考声压级,即在 1kHz 时为 2∗10−5P a[1],通常被认为是人类听力的阈值。
5 结语
希望经过本文的介绍,您已经大致了解了对数与分贝的概念,它们在我们身边的应用远超我们的想象。希望与您共勉,一起探索广袤的知识海洋。
作者:董名轩,香港中文大学(深圳)理工学院
References
[1] Keith Attenborough and Michiel Postema. A pocket-sized introduction to acoustics. Postema,2008, pp. 25-26.
[2] Biamp. GAIN structure: Input and output levels. July 2023. url: https://support.biamp.com/General/Audio/Gain_structure%3A_input_and_output_levels.
[3] Stephen J. Bigelow, Joseph J. Carr, and Steve Winder. Understanding Telephone Electronics. Newnes, 2001, p. 16.
[4] Joseph J. Carr. RF components and circuits. Elsevier u.a., 2005, pp. 45–46.
[5] TechTarget Contributor. What is decibels relative to Carrier (DBC)?: Definition from TechTarget. Mar. 2011. url: https : / / www . techtarget . com / whatis / definition /decibels-relative-to-carrier-dBc.
[6] John H. Conway. Book of numbers. Springer, 2012, p. 249.
[7] Don Davis and Carolyn Davis. Sound system engineering. Sams, 1987, pp. 35–37.
[8] dB to Volts. 2023. url: https://www.extron.com/calculators/db-to-volts/?tab=tools.
[9] Douglas Downing. Algebra, the easy way. Barron’s, 2003, p. 275.
[10] R.V.L Hartley. “”TU” Becomes ”Decibel””. In: Bell Laboratories Record (December, 1928),pp. 137–139.
[11] Kenneth Simonds Johnson. Transmission circuits for Telephonic Communication: Methodsof analysis and Design. Van Nostrand co., 1925, pp. 9–12.
[12] E.R. Kandel. Principles of Neural Science, Fifth Edition. McGraw-Hill’s AccessMedicine.McGraw-Hill Education, 2013, p. 451. isbn: 9780071390118.
[13] Naomi E. Pasachoff. Alexander Graham Bell: Making connections (oxford portraits in science). Oxford University Press, 1996, p. 130.
[14] Robert Sheldon. What is decibels relative to isotropic (DBI)? Feb. 2023. url: https ://www.techtarget.com/whatis /definition/decibels- relative- to- isotropic-radiator-dBi.
[15] Robert Sobot. Wireless Communication Electronics: Introduction to RF circuits and designtechniques. Springer International Publishing, 2021, p. 252.
[16] Qingming Tan. Liang Gang Fen Xi. Zhong guo ke xue ji shu da xue chu ban she, 2005, p. 3.[17] Kuizhi Yue, Shichun Chen, and Changyong Shu. “Calculation of Aircraft Target’s Single-Pulse Detection Probability”. In: Journal of Aerospace Technology and Management 7.3(July 2015), pp. 314–322. issn: 2175-9146. doi: 10.5028/jatm.v7i3.470. url: https://doi.org/10.5028/jatm.v7i3.470.
编辑:黄飞
 电子发烧友App
电子发烧友App














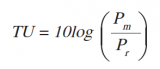














评论