01
第一章:图像配准基本概述
1 图像技术概述
1.1 配准的定义
配准就是对同一传感器不同时间、背景、角度,不同传感器相同时间拍摄的图像进行空间位置的对齐的过程,如图所示:
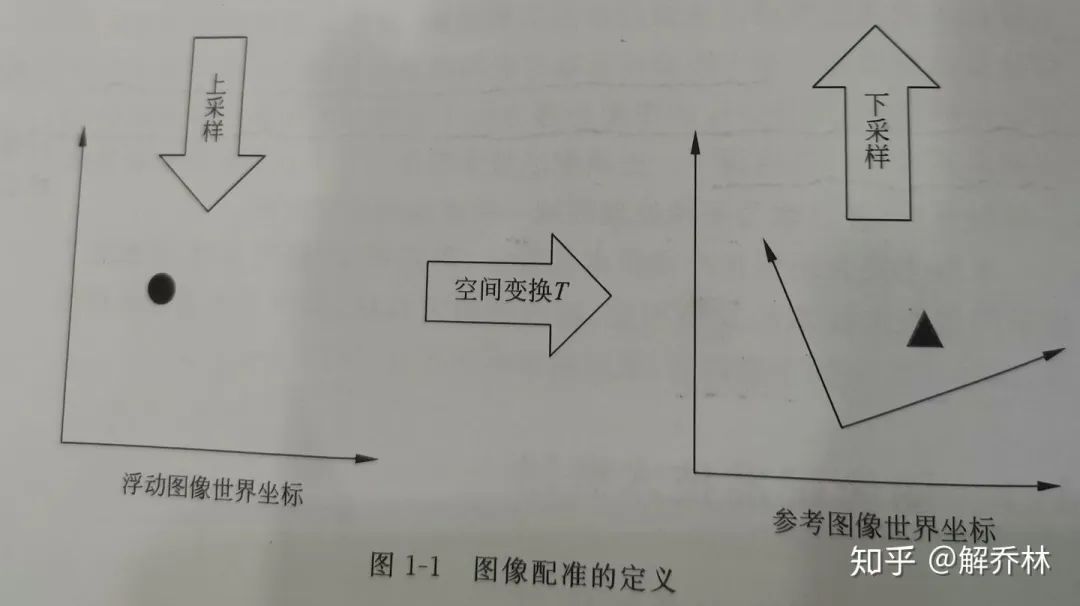
配准的定义
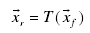
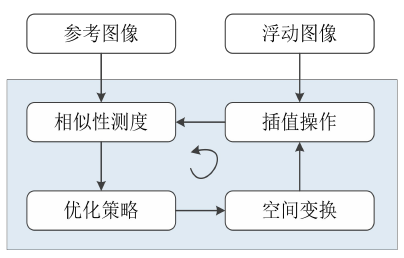
关键在如何找到那个空间变换的T,或者对T的不断逼近
换句话说就是:寻找一个映射关系,让不同图片的点点对应。(像素点的空间位置的一致)
1.2 图像配准的基本框架
医学图像配准算法由下面构成:
特征空间(提取有效信息)
搜索空间(空间变换方式【如何变】)
相似度度量(衡量每次变换的相似性)
搜索策略(下一步该怎么办)构成。
简单来说就是对一个待配的图像提取我们需要的“原材料”【特征空间】 然后用某种方法与被匹配图像匹配【搜索空间】 之后看一下匹配的效果如何?【相似度度量】 最后考虑下一步的变化。【搜索策略】
特征空间【原材料】
特征:图片在不同环境下能有相同的特性、受噪声等外界因素较小的点,被称为图像的特征
特征组成:灰度(灰度值)、直线、轮廓、边、点、面(三维)、角点等等(特征强度也可)
特征空间的重要性:决定了使用那种配准方法
搜索空间(如何变)
空间变换范围【全局变换:增幅图像利用相同的参数变换;局部变换:每个子区域变换】
空间变换模型【刚性变换、仿射变换、投影变换、弯曲变换】
相似性度量(衡量)
特点:相似性度量随着图像配准程度的几何变换而变换(图像的配准,没有固定的度量算法,不断地变化的)
算法:SSD:差值平方和 SAD:绝对误差和 NCC:归一化互相关 MAI 互信息 基于香农熵的、基于信息论的相似性度量
搜索策略(下一步如何走)
因为图像的配准是一个多参数问题(多个特征点匹配),难以n全其美。所以如何找到局部极值点的情况下找到一个最优的空间变换参数,是配准的关键(就是解决n全其美的关系)
常见的:最小二乘法、Powell法、下山单纯形法、Levenberg-Marquadrt 法、Newton 迭代法、共轭梯度法、随机搜索法、最速下降法、松弛匹配法、遗传算法和模拟退火法等
相关文章参考:
优化算法综述:https://zhuanlan.zhihu.com/p/272656135
1.3 配准方法的分类

1.4 图像配准的意义
通过医学成像,可以无创伤的获得人体的组织和器官结构信息以及功能信息。
分类
1)解刨图像
特点:描述人体的组织和器官
CT图像,黑影代表着低吸收区,白影代表着高吸收区。(黑白:组织的厚度及其密度)
虽然对软组织、骨骼等特清晰,但是它对人体有辐射
MRI:虽然性能中间,而且没有害,但是费用很高,有伪影,而且时间长
2)功能图像
特点:描述不同状态下人体的组织器官的活动状况。
反映了他的内部化学状况以及代谢状况,根据不同时间的图片配准,可得知这段时间疾病恢复的怎么样。也可以进行早期诊断(内在影响外在)。
具体原理是:计算机断层成像技术(ECT),通过γ射线成像,反映了放射性的核素的分布,进而得知他的形态。越清晰就越健康。
1.5 图像配准的应用领域
视觉模式识别、医学图像分析、地球遥感影像、国事与国防(军事目标的检测、识别、跟踪)。
2 医学图像配准技术
2.1 医学图像配准的发展历史
基于解刨结构特征点的配准【人工】
采用人工的特征点配准,利用迭代最近领点、欧氏距离等。一般只适用于单模态,而且准确率不高、具有主观性
计算机辅助基于图像特征的配准配准【计算机】
借助计算机实现图像的配准。外部特征和内部特征两种方法
外部特征:用支架、皮肤标记法等标记
内部特征:图像采集点匹配后在对其进行配准
基于灰度的多模态的医学图像配准
新生很多技术对人体进行图像生成(CT、MRP、PET等),这个时候需要找出一个衡量不同模态的相适度测量,对其不同模态间具有鲁棒性(稳定性)
基于信息论:联合墒(基于概率分部随机性,但是对噪音比较敏感);互信息(可以自动实现,不需要对其进行分割。它基于图像含有对方的信息的多少。)
基于灰度图像:相关性配准【两幅图像灰度定值时,存在相同类似的】;Demons算法的非刚性医学图像配准【非相似性度量!是搜索空间~刚性配准】
基于特征空间:基于熵图的配准;基于结构特征的多模态医学图像配准
基于三维的图像来说,比较耗费时间,学者提出了由粗到精的分层配准。避免陷入局部最优点。
基于模型的非刚性配准
非刚性:就是柔弱的,例如人体、线虫这种。
PDE:基于偏微分方程的配准
偏微分方程或相似性度量的构造(光流、流体力学、扩展模型)
Demons是比较有名的算法。(简单来说就是把图片套上一个网格,根据特征点对网格进行变换)
FFD:基于B样条自由形态形变模型的配准(也是一个网格,但是是一个非均匀的网格,进而控制形变的精细程度和大小)
2.2 医学配准的现状(当前技术与难题)
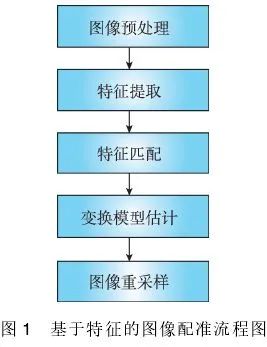
分类(是否在图片中找明显的特征点)
1)基于特征提取的[1]
1、 基于外来特征【人工】
优点:技术量小,速度快
缺点:但是依赖于人工的标记等,只适合刚性配准
2、 基于图像内部特征点
寻找配准图像的几何变换。图像的特征点提取后进行配准
三维图像的配准,基于最小化距离准则进行快速的配准
矩不变量配准:一般对数字减影血管照影图像配准
2)基于灰度提取的「技术量大,复杂」
迭代优化一个相似度测量进行寻找待配准图像的图像转化。(类似于深度学习,不断的重复重复直到达到某一个标准)。
常用的相似度测量包括:
灰度差异
灰度差异需要相同的灰度,一般用于单模态的配准「差值平方和以及归一化形式」
互相关
一个图像中包含另外一个图像的内容。并不可以处理灰度分布不均匀的图片。
信息论(互信息)
他是一个包含关系,包括互信息在内的很多测量。【提前估计两个图片的概率分布,并不需要特征提取和分割、线性关系】
发展:互信息-》归一化互信息-》信息测量-》信息熵-》广义墒的信息论测度-》散度测量
像素间的空间信息问题:高阶互信息等
为了更好的利用图片的空间信息:
RMI:局部互信息。线性加权,降低其局部灰度的变化,引起起配准误差
cMI(条件互信息):增加其鲁棒性以及精确度
SEMI(空间编码互信息):进行局部相似的判断衡量整体
总结:将其特征与基于灰度的结合在一起是常用的。采用字典学习(标签)、K近领图(多特征互信息)、特征领域互信息(空间与结构信息)、待配准的图像局部结构自相关作为相似度。
2.3 常用的配准、相似性度量方法
基于灰度的图像配准(均方差、相关系数、互信息、Demons配准)【灰度】
基于变换域的图像配准【傅里叶变换】
基于图像特征的图像配准(只针对图像中重要的点和图像进行匹配【角点、等等;surf、ORB、HOG、LBP】)
1、刚体
它的变形参数较少
对于三维图像,其3个平移量,3个旋转量
效率较高、速度较快。但是其在医学上用处不大
2、非刚体
单纯特征点并不适用多模态图像
利用灰度信息以及基于灰度的医学图像配准方案省下了各种步骤,而是把待配准图像间的灰度值的差异作为相似度度量。
方法:SSD(差值平方和)、SAD(绝对误差和)、SSC
1)基于灰度的医学图像配准
(SSD、ρ等略)
特点:必须记录概率密度
香农熵
累计概率分布(CRE):相对于香农熵来说,适用于连续或者离散、具有更普遍的性质。
互累计概率熵(c-CRE):应用于刚体/非刚体中,具有更高的噪音免疫性。
互信息的研究分为两组(都是处理多模态医学图像的效果)
【熵的估计不同】:
非参数估计
直方图估计
优缺点
优:对灰度不敏感、鲁棒、精确、不需要对图像分割等
缺:(不具有重叠不变性)不会随着配准图像视野的变化而变化。
改进
归一化相似度测量
人们猜想互信息可能还是欠约束的,陷入了局部最优点里面。
人们提出了相关比率(CR)做相似度测量,具有较好的精确性和鲁棒性
f信息测度(核函数)
核函数能够精确的配准(一般用B样条核函数)
联合分布散度
2)针对空间信息的测度方法【图像特征】
上述方法都只考虑单像素配准忽略了图像空间信息。这个时候需要将局部信息融入到相似度准则中
变分方法(解决灰度不稳定的问题)
图形梯度(得到互信息、联合熵、边缘熵的表达式,通过最大局部相似度进行配准)
局部互信息(RMI)【线性加权,降低灰度值的变化引起的配准误差】
条件互信息(cMI)(第三维代表联合灰度比,性能更加优越)
空间编码的互信息(SEMI)【用自由形变的坐标作为空间变量,然后再对其附近的区域进行局部相似度测量,这些数字就是空间编码的互信息】
高阶信息论测度(将局部几何信息的附加特征融入相似度)
梯度项*互信息
领域像素间的灰度重生编码局部信息
随机线和减少直方图箱子的方法
采用图像块的字典学习
任意两灰度变化的平均比率构建新的特征场
最小生成树
熵图
K最近领域算法
相位信息用于非刚性医学配准
相位互信息
基于物理的超声图像
获取目标灰度与原灰度的条件概率
熵图像及流体学习
相邻图像块的相似度
相关文章参考:
图像配准传统算法总结https://mp.weixin.qq.com/s/sVXn7AsogmyKIuEmAcldoA
02
第二章:医学成像技术
医学图像分为两大类:解刨图像和功能图像。
解刨图像描述了人体生理解刨结构的信息,而功能图像反应的是机体内部的生理、生化等功能代谢信息。

前言
医学成像技术是某种能量发射物质下,医学成像链的形成以及影响其因素的原因。
通俗来说就是物质(元素)都会发射不同的能量,通过检测区分这些能量,就可知道其内部构成。
2.1 X射线
简单来说就是照射人体,穿透后接收X射线,出现不均匀的着色,形成的轮廓
1)X射线的发现--伦琴。众所周知,别名伦琴射线
2)X射线:
真空的、高速运动的电子撞击金属内部外层电子,跃迁释放的能量
条件:电子源、强电场以及高速运动的电子流,适当的阻挡物去接受被释放的能量
原理:电能转化为动能
分类:【能量少的,波长长,穿透力不强反之】
能量大:金属钨,用于X射线的诊断和治疗(硬射线)
能量少:金属钼,用于软组织成像(软射线)
3)属性
物理属性:穿透(X射线不吸收),荧光(受X射线后发生了跃迁),电离(X射线照射后发生了电离)。
化学属性:卤化银感光(根据不同的光度分辨不同的人体器官),着色(实际上应该叫褪色,结晶脱水,之后发生褪色,不同的组织褪色不一样)。
生物属性:人体接受X光照射后会产生损害、抑制细胞分裂、细胞坏死。
4)影响成片的因素:电压、电流、时间、焦距;人体照射的姿势、成像的方式。
2.2 数字X射线成像(模拟成像、数字成像)
简单的来说就是加入了计算机,能够存储!!!
X技术+计算机=图像->数字图像->记录处理:主要是利用了计算机对其图像进行存储、转化、处理等。
模拟成像:针对连续函数,结构逼近法。
数字成像:针对离散函数(单像素大小以及灰度值)【数字化:坐标数字化以及灰度数字化】。
分类:
CR成像技术(计算机X成像技术):信息采集、转换、处理、存储成像。
DR成像技术(数字化X成像技术):直接数字化成像技术、间接数字化成像技术、CCD X射线成像技术、多丝正比电离成像技术。
2、成像技术
1)CR成像技术【光激励存储荧光体成像】
光激励存储荧光体->利用延迟发射特性->(再照射)释放能量->探测器获得并存储->转为数字信号再记录->处理
总结一下就是信息采集、转换、处理、存储成像。
利用的技术:对比度处理(增强对比度【显著性】)、频率处理【傅里叶滤波等】、动态范围控制、体外伪影抑制、能量减影。
2)DR成像技术【数字化X摄像系统】
优点:更高的分辨率、效率高、低X照射,无害、图像层次丰富。
直接数字化X成像(金属硒)
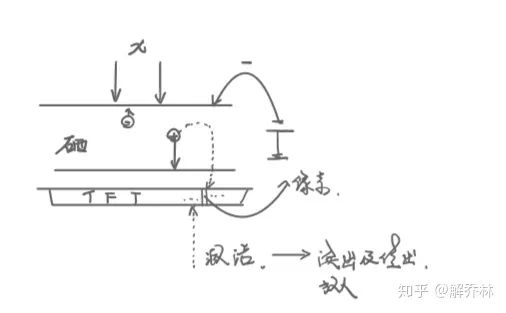
成像图解
间接数字化X系统(金属铯)
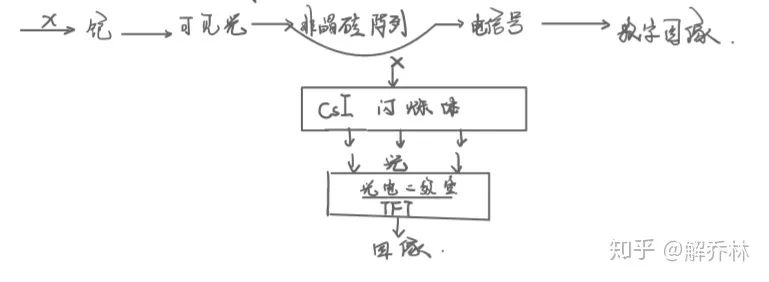
成像图解
CCD X 射线成像系统

成像图解
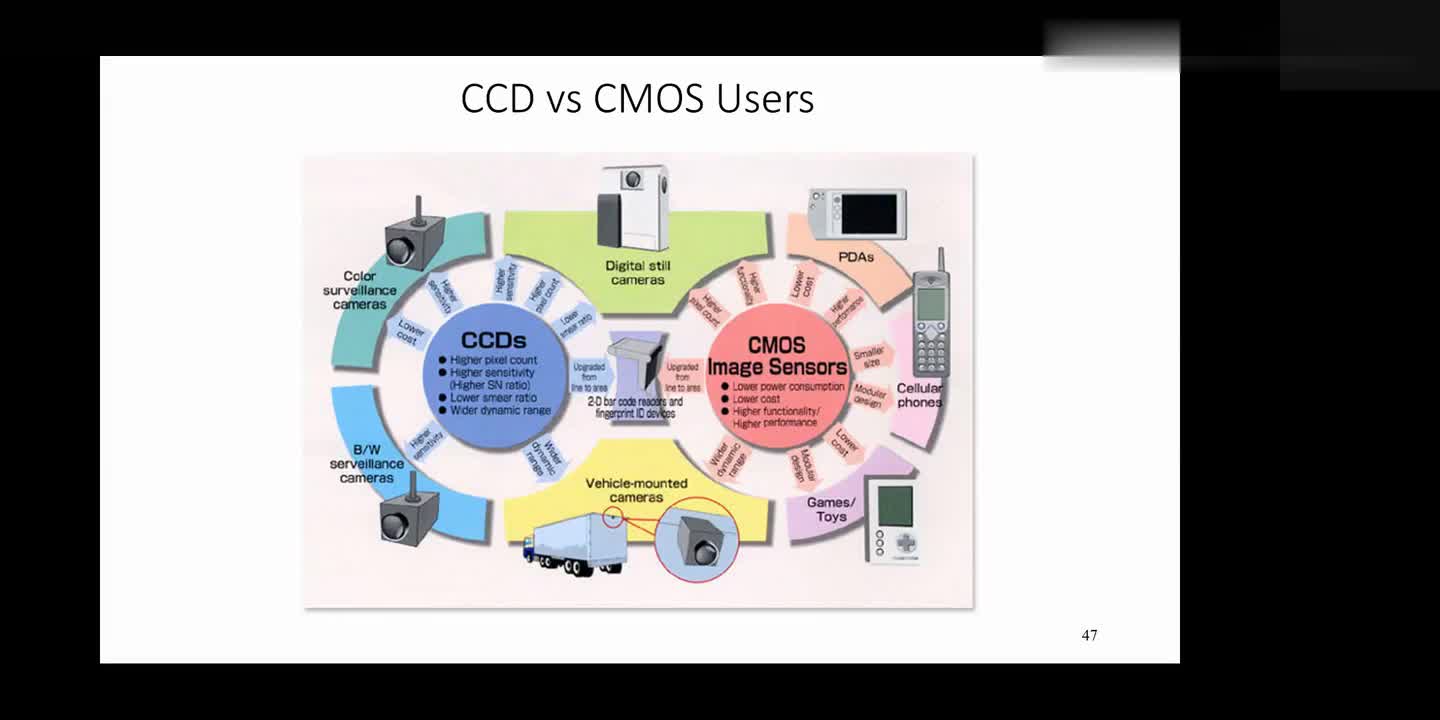
注:CCD结构是大量的光敏组成的点、线、面阵
多丝正比电离成像
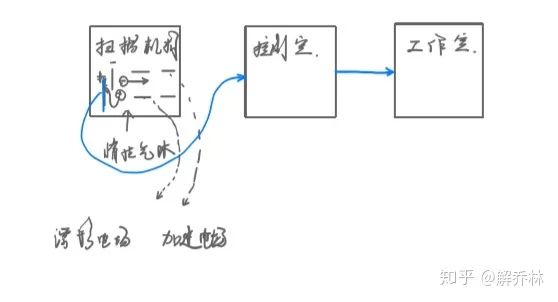
成像图解
优点:扫描X射线剂量低、面积大。
原理:正负电极以及加速电场、偏移电场。在充满惰性气体的盒子里,负电子的离子云飘向正级,产生了脉冲,通过某种方法被记录下来。
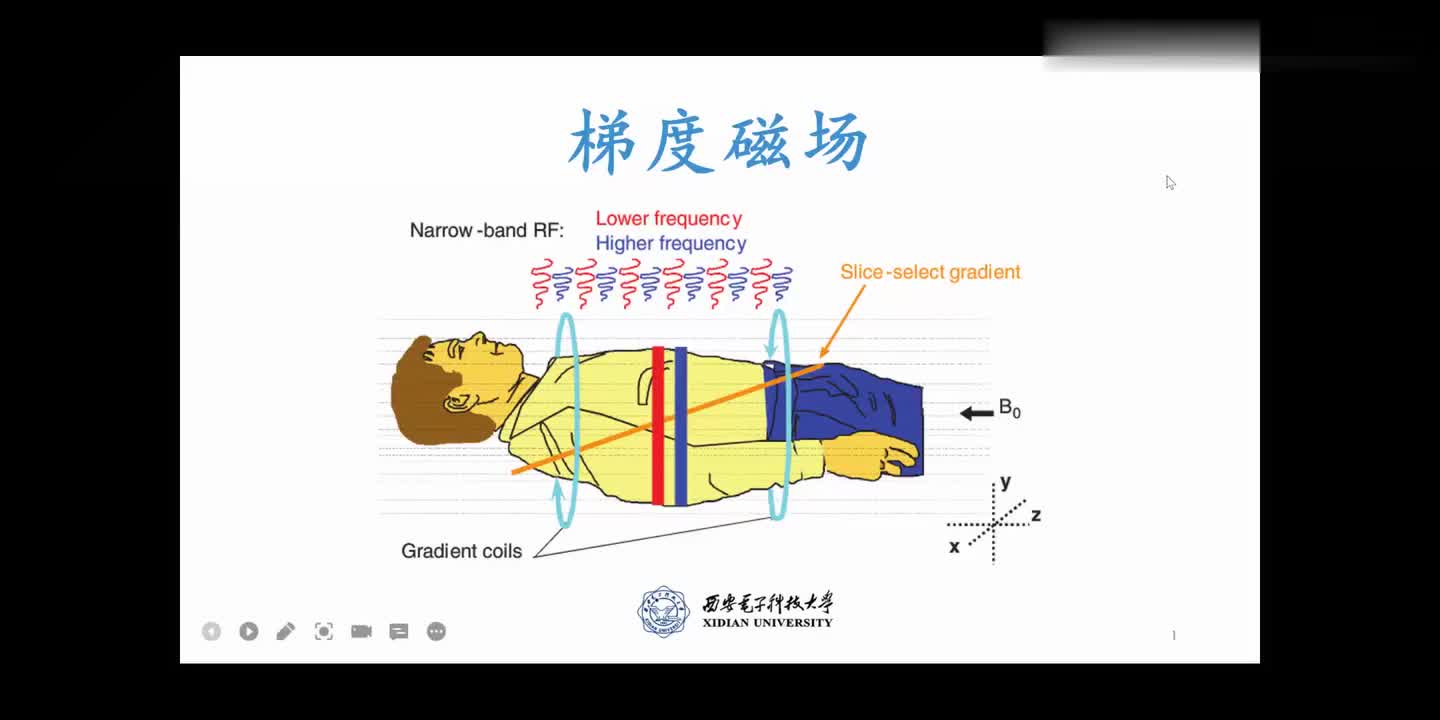
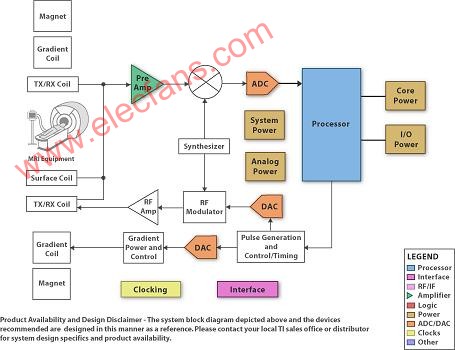
2.3 磁共振成像技术(NMR)
简单的来说就是对氢核的共振,发送射频,成像。
优点:
体积小,质量好,速度快
组成:
通过磁体系统、梯度系统、射频系统、计算机系统组成的,根据计算机的信号的产生、探测、编码、图像的采集、重建、功能模板的有机组合构成。
原理
人体各组织含有的氢化物和水含量不同
进而对人体射频(RF),人体氢核发生了磁共振现象
停止RF后,氢核向外发送射频信号(弛豫)
因为不同的氢核,产生的RF的强度不同
成像
优点及其应用
对软组织有极佳的成像效果
多参数成像(多种组织特征参数的函数)
多方位成像(横截面、矢量图等)
大视野(可知水、软组织、脂等)
无辐射、无创伤
多用于对人体代谢的研究
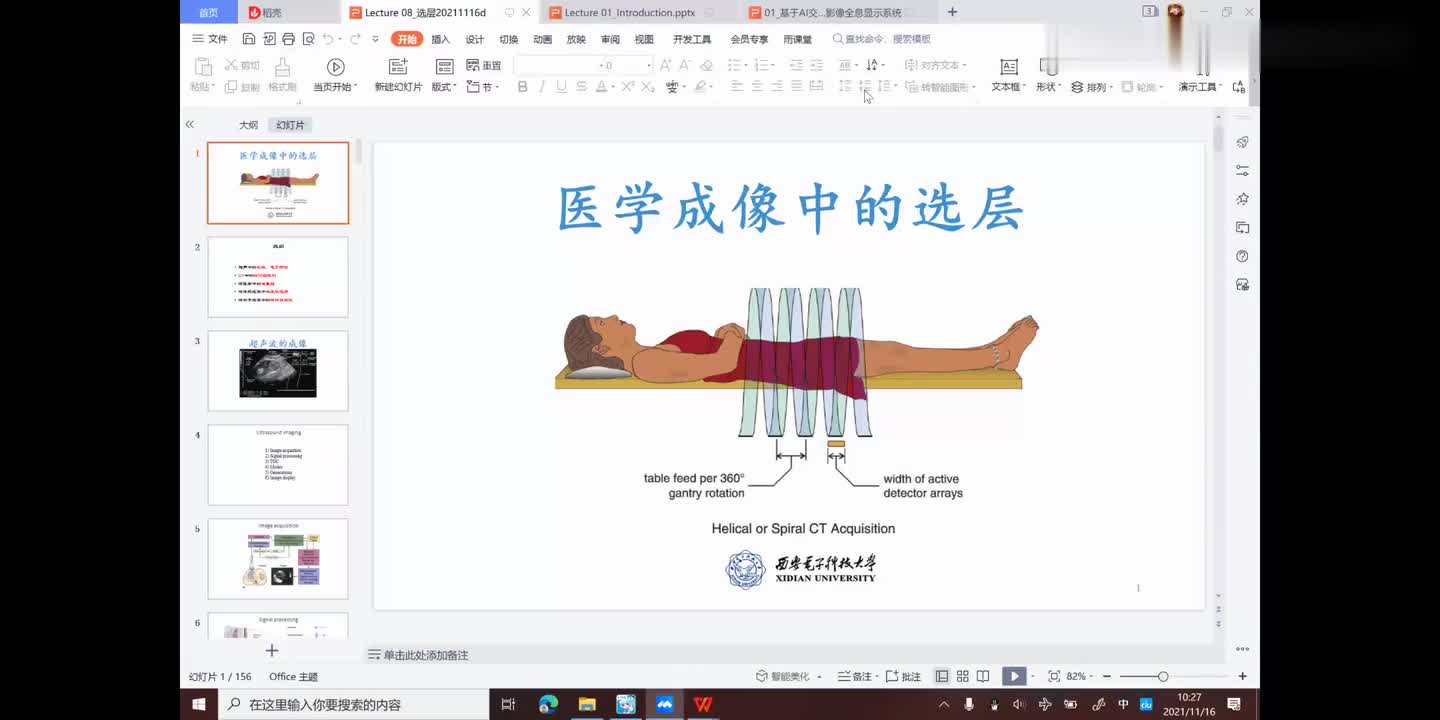
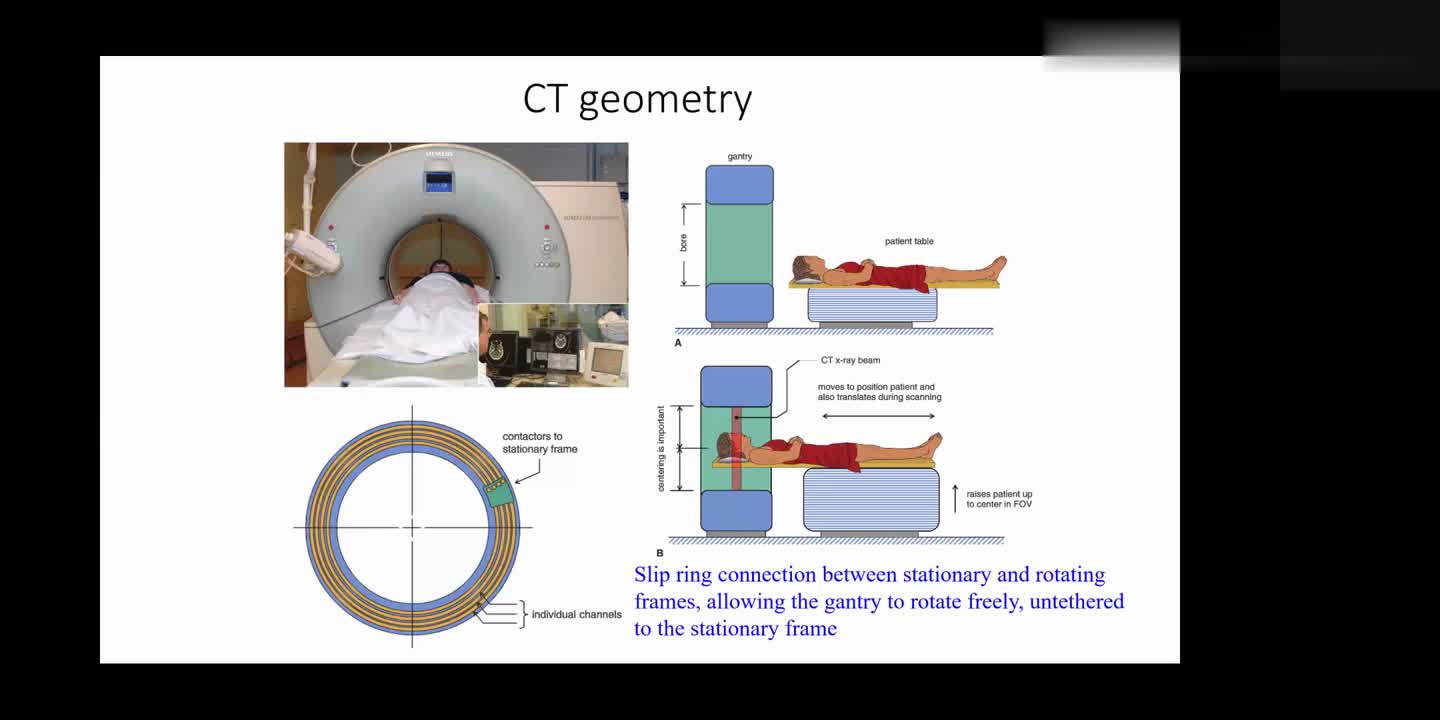
2.4 CT(计算机断层扫描)
X射线技术的一个升华,断层扫描更加的立体化
优点:解决了X光影像重叠问题,分辨率高、定位准确、清晰

成像图解
多方位X光多一定厚度的层面扫描,透过X光的由接收器接收后产生信号存储
缺点:是否对人体有害暂无定论
2.5 核医学成像
ETC(PET、SPECT):发射式计算机断层(正电子放射断层、单光子发射计算机断层)
1、PET:功能:分析人体的组织结构功能信息(例如血液现象、人体的新陈代谢)
原理:将放射性元素注射入人体后,检测它的流动情况(会在不同地方聚集)
缺点:时间长、分辨率低
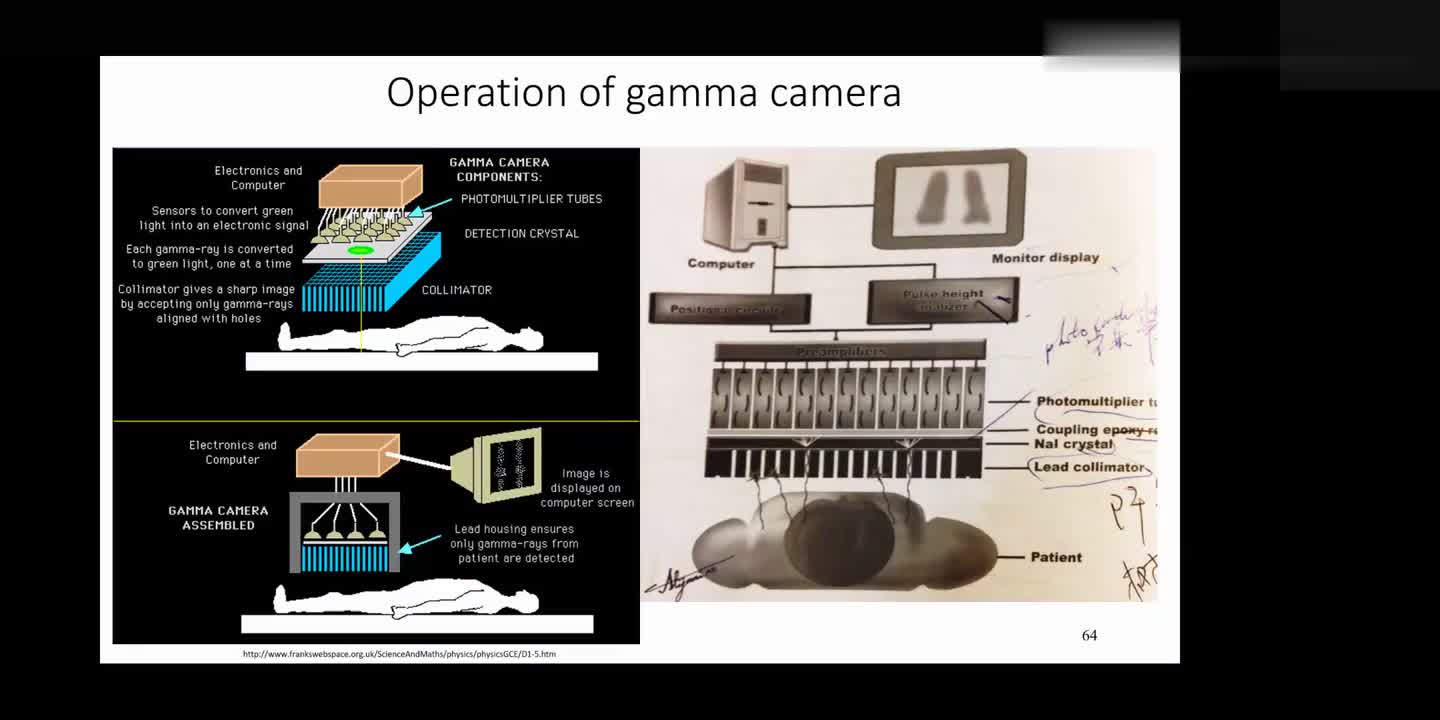
2、SPECT:
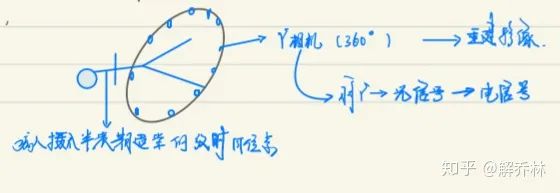
成像图解
原理:病人摄入放射性元素,用γ相机360度照射后,获得影像数据。
特点:相较于CT、MRI来说,它可以反应器官的功能变化,非常有利于前期诊断。(早期外在没有体现的时候,检查其内部的功能是否紊乱)
2.6 医学超声图像(USI)
利用声波的反射
介绍:超声图是通过向人体发送超声波,收集放射信息,获得人体内部信息的手段
分类:
根据成像原理:
A(利用波幅高低反应人体)【A波回声图】
B(记录人体内部的灰度图像):以光电进行表达的截面图。【B型二维成像】
M(心脏):组织随时间的变化而变化的一维图像空间结构【M心动图】
多普勒成像:是对运动的物体产生的信号,进行分析
D【D型超声诊断】
三维成像:就是n个二维在计算机合成下的三维
根据反射声波的多少:
无反射(人体的液体质地均匀):利用这个原理可检测肝、肾等的囊肿。
少反射:检测心脏、肝等大部分器官。
多反射:存在不均匀的结构,反射较多。(瘤)
全反射:检测气体病变。
03
第三章:图像匹配算法步骤及详解
概论:配准匹配算法就是寻找配准图像间的最优变换参数。由特征空间、搜索空间、相似度度量、搜索策略四个部分组成。
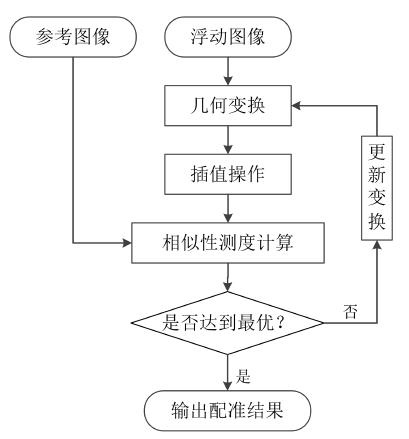
步骤:拿到一个图像,先各种变换(刚性变换、非刚性变换、仿射、投影、弹性),然后对其进行特征空间的提取(点、线、面、梯度等),然后提取后,用其进行比较(相似度度量),看配做后效果如何(比如有50%的相似度等),最后进行搜索度量【下一步该怎么办】。
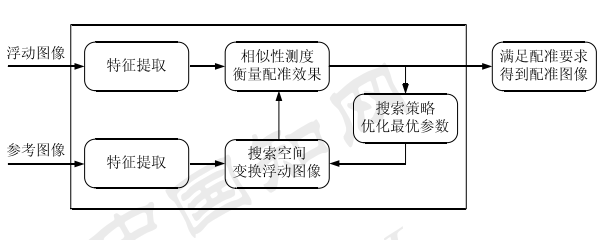
从其了解到,他是一个迭代的过程,如图所示:

图像配准迭代
3 搜索空间【配准算法】
3.1点测量:【通过响应R判断是不是特征点】
灰度级间断检测技术:1、系数X灰度级 2、孤立点检测

中心区域响应计算
R是中心区域的响应,根据附近的8个位置,按照一定的系数X灰度级计算。

判断是否是特征点
判断:如果孤立的点和领域的差距过大,而且附近都是光滑的,它就是特征点了。
3.2 线测量【响应的关系】
同样如上面似的计算R值,然后如图:
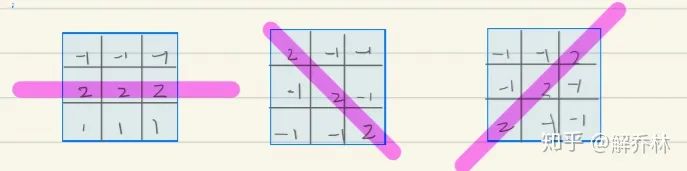
3.3 霍夫变换【计算机判断表示直线】
霍夫变换相关解释:
https://zhuanlan.zhihu.com/p/47649796
简单介绍:
一条直线,计算机并不知道也找不出来,也确定不了。计算机是0101存储的。如何知道某一个点在这条线上?
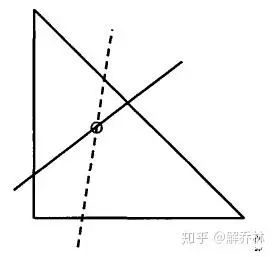
研究发现,将直角坐标系改为极坐标,会发现所有的点在转变为极坐标是一条线,并且这些曲线交于一点[2]。
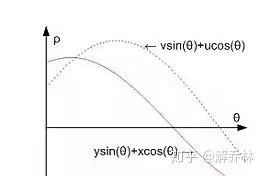
简单来说就是,很多点的极坐标只要交于一点,就说明他们是在一条线上。
缺点:处理时会丢失信息。
3.4 边缘检测【通过变换的快不快(梯度)判断是否是特征点】
边缘z中蕴含着很多信息,如梯度、方向、形状!
现有以下检测算法:
1)梯度算子(找下降的是否平缓)
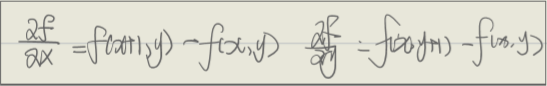
带入到:

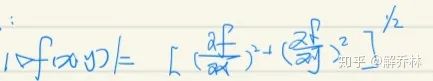
2)罗伯特梯度法
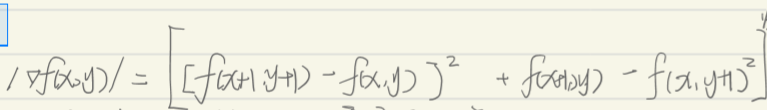
只能算出大概轮廓,但是精确度不高
3)拉普拉斯算子:
对其进行二阶导数之后
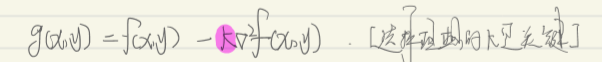
阈值比较
放大其差距,更好的找出其特征!
3.5 Harris角点【试探,偏移-大变】
存在一个点,向任意一个地方偏移一点点,会产生很大的变化【角点就是轮廓之间的交点】
类似于:桌角、门角等
步骤:
1)计算自相关函数以及自相关矩阵的特征值[3]
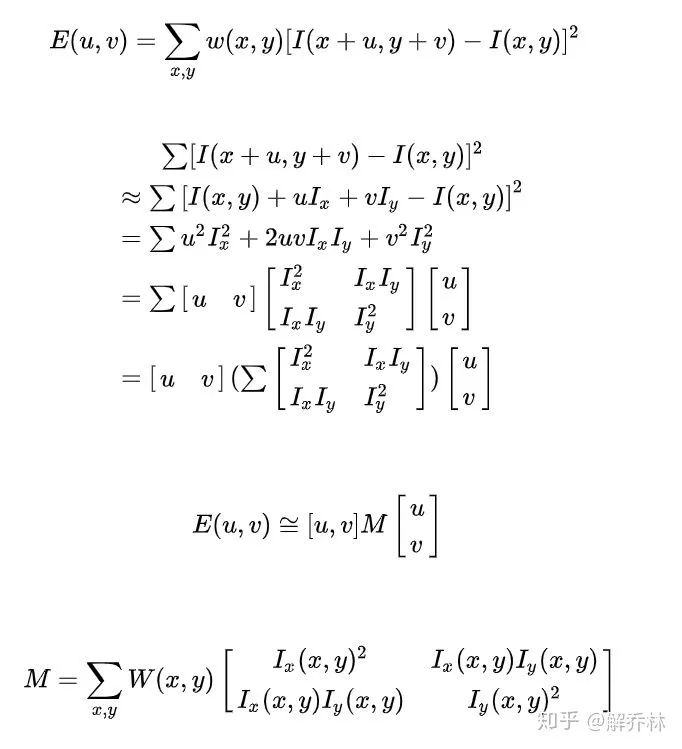
结论:
平坦区域:梯度方向各异,但是梯度幅值变化不大
线性边缘:梯度幅值改变较大,梯度方向改变不大
角点:梯度方向和梯度幅值变化都较大
2)计算R
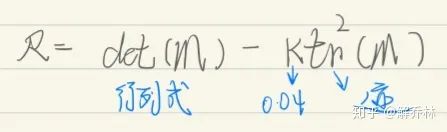
其中:
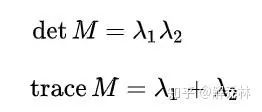
λ1 :X轴方向的偏导的特征值;
λ2 :Y轴方向的偏导的特征值
3)判断

如果矩阵对应的两个特征值都较大,那么窗口内含有角点
如果特征值一个大一个小,那么窗口内含有线性边缘
如果两个特征值都很小,那么窗口内为平坦区域
3.6 SIFT特征点:【尺度不变特征变换】[4]
在不同的尺度空间上查找关键点,并计算出关键点的方向。
先理解两个要点:一是图像可用很多种方法表示,如在RGB空间内的表示方法就是颜色(r,g,b),梯度空间就是用梯度表示。梯度空间就是某一个像素的梯度方向的表示,用0-359°表示。
优点:SIFT算法是一种基于局部兴趣点的算法,因此不仅对图片大小和旋转不敏感,而且对光照、噪声等影响的抗击能力也非常优秀,因此,该算法在性能和适用范围方面较于之前的算法有着质的改变。
步骤:[5]
1、尺度空间极值检测【候选关键点】:通过使用高斯差分函数来计算并搜索所有尺度上的图像位置,用于识别对尺度和方向不变的潜在兴趣点。
2、关键点定位:通过一个拟合精细的模型在每个候选位置上确定位置和尺度,关键点的选择依赖于它们的稳定程度。
3、方向匹配:【直方图】基于局部图像的梯度方向,为每个关键点位置分配一个或多个方向,后续所有对图像数据的操作都是相对于关键点的方向、尺度和位置进行变换,从而而这些变换提供了不变形。
4、关键点描述:在每个关键点周围的区域内以选定的比例计算局部图像梯度,这些梯度被变换成一种表示,这种表示允许比较大的局部形状的变形和光照变化。



3.7 SURB算法
SURB算法是对SIFT的一种改进。更加高效的进行特征的提取以及描述。
1)建立Hessian矩阵【用于更好的提取特征点】
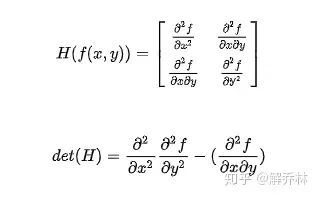
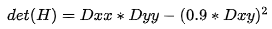
det(H)这个值代表着斑点响应,计算得到不同尺度下的最大值和特征点。
2)构建尺度空间[6]【发现轮廓,避免一叶障目】
关于尺度空间的理解:www.cnblogs.com/lzhu/p/8430355.html
“尺度空间”的概念就是在多个尺度下观察目标,然后加以综合的分析和理解,进而发现我们所感兴趣的事情。
同Sift一样,Surf的尺度空间也是由O组L层组成,不同的是,Sift中下一组图像的尺寸是上一组的一半,同一组间图像尺寸一样,但是所使用的高斯模糊系数逐渐增大;而在Surf中,不同组间图像的尺寸都是一致的,但不同组间使用的盒式滤波器的模板尺寸逐渐增大,同一组间不同层间使用相同尺寸的滤波器,但是滤波器的模糊系数逐渐增大。
下图不同距离的尺度空间的过滤:
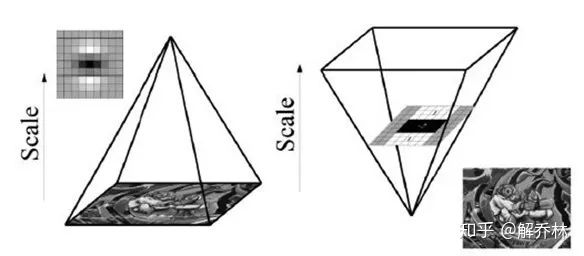
3)确定特征点
特征点的定位过程Surf和Sift保持一致,将经过Hessian矩阵处理的每个像素点与二维图像空间和尺度空间邻域内的26个点进行比较,初步定位出关键点,再经过滤出能量比较弱的关键点以及错误定位的关键点,筛选出最终的稳定的特征点。
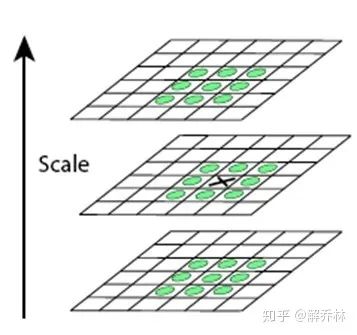
4)特征点主方向分配
Sift特征点方向分配是采用在特征点邻域内统计其梯度直方图,而在Surf中,采用的是统计特征点圆形邻域内的harr小波特征。
在特征点的圆形邻域内,统计60度扇形内所有点的水平、垂直harr小波特征总和,然后扇形以一定间隔进行旋转并再次统计该区域内harr小波特征值之后,最后将值最大的那个扇形的方向作为该特征点的主方向。
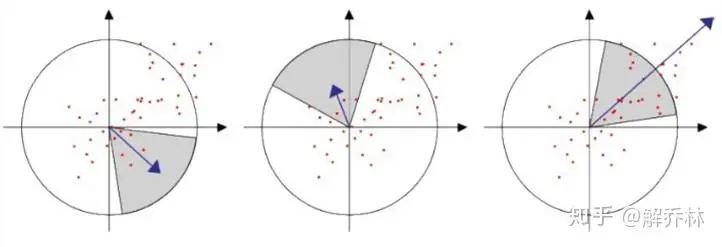
5)生成特征点描述子
在Sift中,是取特征点周围44区域块,统计每小块内8个梯度方向,用着44/8=128维向量作为Sift特征的描述子。
Surf算法中,也是在特征点周围取一个44的矩形区域块,但是所取得矩形区域方向是沿着特征点的主方向。每个子区域统计25个像素的水平方向和垂直方向的haar小波特征,这里的水平和垂直方向都是相对主方向而言的。该haar小波特征为水平方向值之后、垂直方向值之后、水平方向绝对值之后以及垂直方向绝对值之和4个方向。
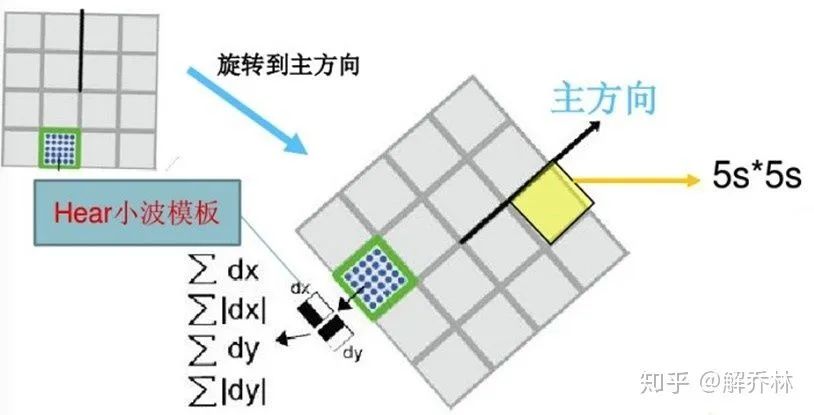
6)特征点匹配
与Sift特征点匹配类似,Surf也是通过计算两个特征点间的欧式距离来确定匹配度,欧氏距离越短,代表两个特征点的匹配度越好。
不同的是Surf还加入了Hessian矩阵迹的判断,如果两个特征点的矩阵迹正负号相同,代表这两个特征具有相同方向上的对比度变化,如果不同,说明这两个特征点的对比度变化方向是相反的,即使欧氏距离为0,也直接予以排除。
特点
Sift算法的优点是特征稳定,对旋转、尺度变换、亮度保持不变性,对视角变换、噪声也有一定程度的稳定性;缺点是实时性不高,并且对于边缘光滑目标的特征点提取能力较弱。
Surf(Speeded Up Robust Features)改进了特征的提取和描述方式,用一种更为高效的方式完成特征的提取和描述。
3.8 HOG(方向梯度直方图)
HOG特征描述子是在一个网格密集、大小统一的细胞单元上进行计算,而且为了提高性能,它还采用了局部对比度归一化思想。它的出现,使得目标检测技术在静态图像的人物检测、车辆检测等方向得到大量应用。
它首先把一副图像划分成若干个块,然后再把块划分成若干个单元,然后对单元内部的像素进行梯度统计。
梯度计算
先找其梯度特征
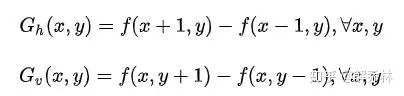
偏导
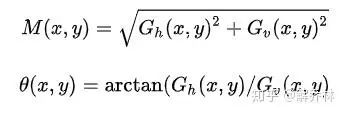
梯度值(梯度强度)和梯度方向
单元划分

分为很多块,每一块又有很多细胞。每个细胞单元中对内部的所有像素的梯度方向(0-180°,分为9部分)进行统计,建立直方图:
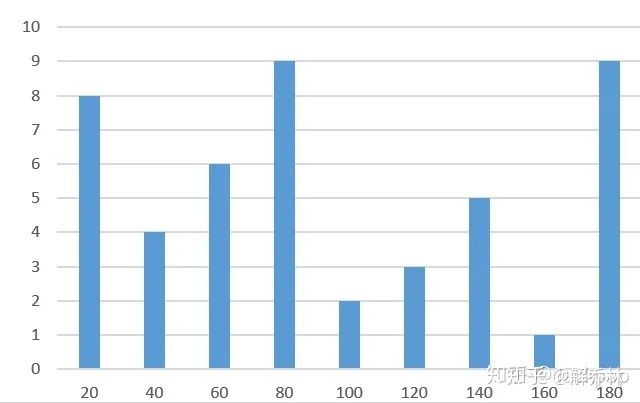
方向直方图
区块选择
3*3或者6*6个像素、像素选择9个通道
区间归一化
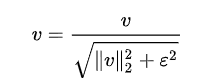
SVM分类器
前面提取的图像特征向量进行训练,寻找一个最优超平面作为决策函数,得到目标的训练模型。
3.9 DPM(可变型部件模型)[8]
就是更多维度下的训练、检测以及SVM
类比于HOG,
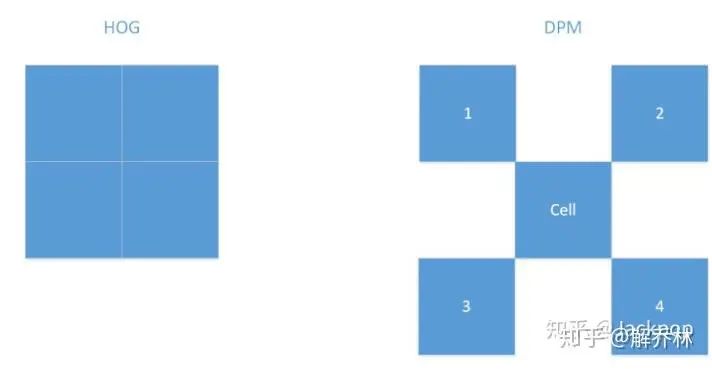
DPM不仅提取结合0~180度方向不敏感特征和0~360度方向敏感特征两种特征,它首先提取0~180度之间的特征,得到上图所示4*9维的特征,拼接起来得到13维特征向量,然后再提取0~360度之间的特征,得到18维特征向量,二者相加得到31维特征向量。
1、模型训练(初始化、合并组件、初始化部件)
2、模型检测(特征提取、计算根滤波器和部件滤波器的得分、合并根位置的得分,得到总得分)
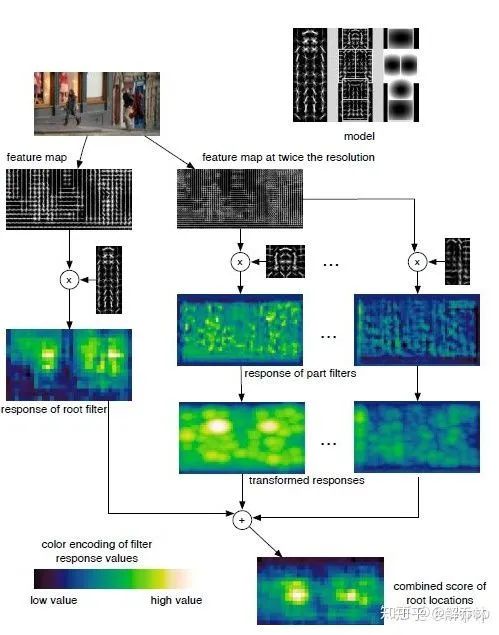
3、Latent SVM
3.10 传统目标检测之卷积神经网络概述[9][10]
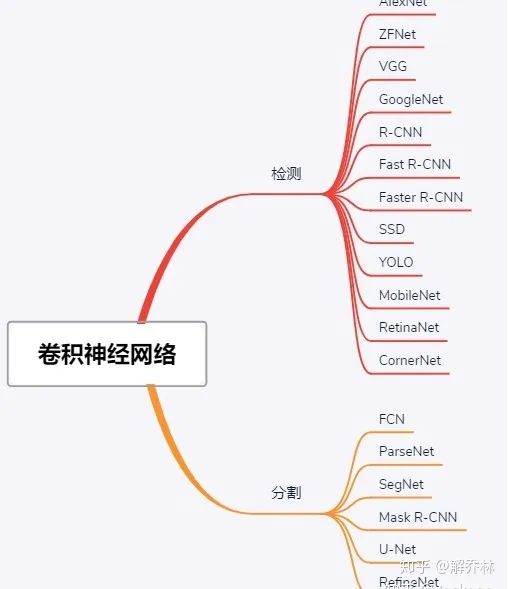
检测就是判断一幅图像是否有特点的目标以及位置
分割就是识别并分割其边缘(像素上的分割、语义上的分割)
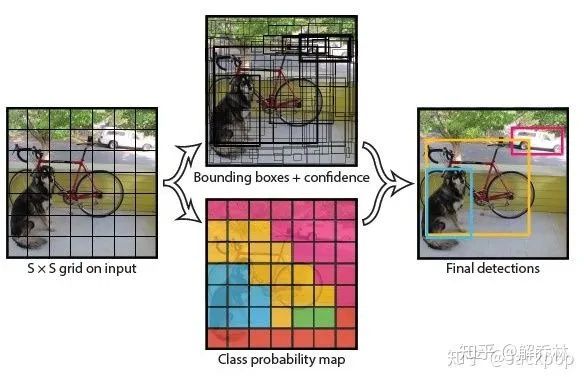
所用到的技术:
卷积、池化(特征提取)
基础块(网格)
Dropout【丢掉】(针对过拟合)
跳跃连接【防止梯度消失于梯度爆炸】
锚点
优化算法【梯度下降、Adam、牛顿法等,加速】
激活函数【解决模型的线性不可分问题,把非线性的特性引入到网络模型中】
批量正则化【加速模型的收敛,避免深层神经网络的梯度消失和梯度爆炸】
回归
CNN的模型架构:
输入层
特征提取层
全连接层【对特征层进行后处理】
回归
输出层
如何搭建?
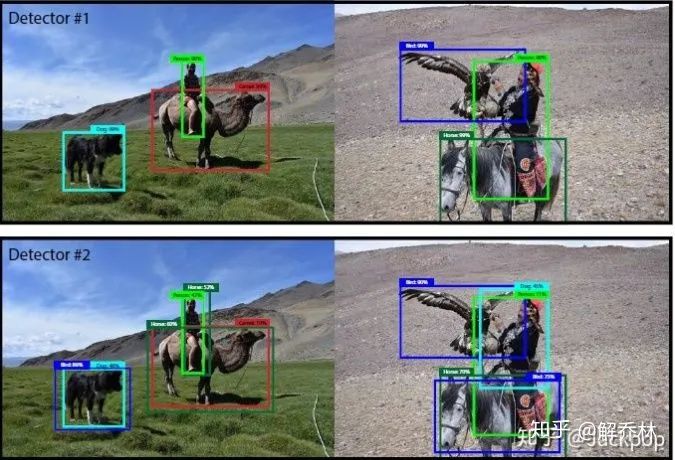
数据获取
数据预处理
模型搭建
数据后处理
04
第四章、特征空间
空间变换范围:全局变换、局部变换
空间变换模型:刚体变换、仿射变换、投影变换、弯曲变换(非线性变换)
4.1 刚性变换(只允许平移和旋转两种)
公式:P( x)= Ax+ b
变换后任意两点的距离不变,旋转变换利用下面矩阵:
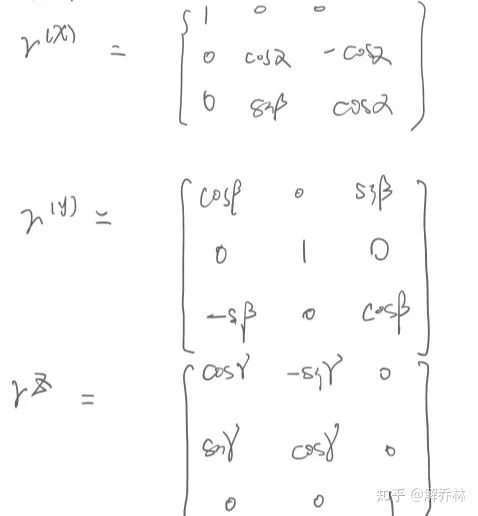
4.2 仿射变换(尺度和剪切变换)【正方形变成平行四边形】
原来平行的线还是平行,利用以下矩阵:

tX y z表示xyz方向上的位移
4.3 投影变换【用于三维->二维的变换】
他不再保持平行性
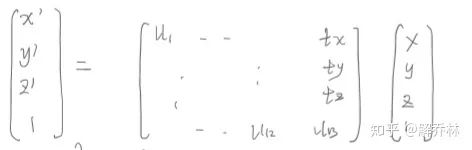
4.4 弯曲变换
用的最多也是最难的一种,有一个映射,使得直线变成了曲线(x',y')=f(x,y)
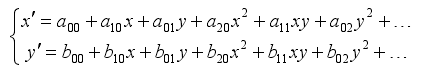
下图是四种变化的图例:
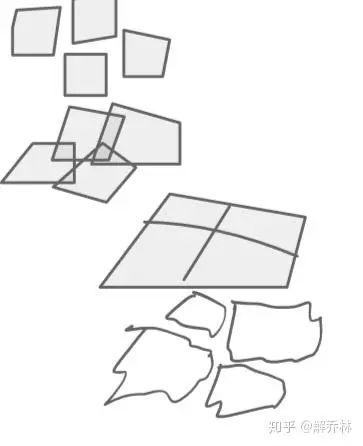
4.5 比较
05
第五章、相似度度量
简介:相似度测量简单的来说就是利用某种方法评估一下这次的配准的效果如何。
算法:
差值平方和、绝对误差和、归一化互相关、相关比率、互信息测量
5.1 差值平方和
就是配准后相同位置灰度值的差值的平方和
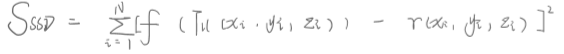
5.2 绝对误差和
就是上面那个不平方,改为绝对值
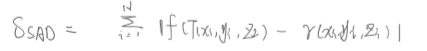
5.3 归一化互相关
利用平均值误差来度量
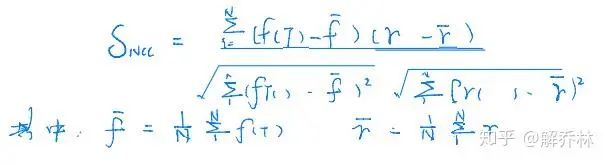
5.4 相关比率
在参考图像下,浮动图像的条件概率【后面详解】

5.5 互信息测量(MI)
看配准图像与被配准图像的依赖程度【后面详解】:可以表示一个图像包含另一个图像的多少
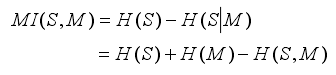
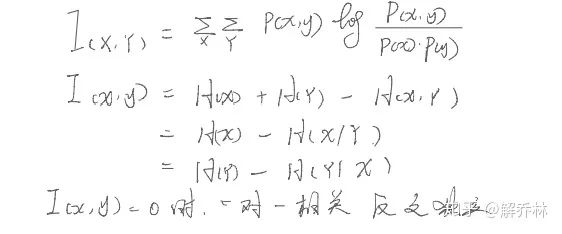
5.6 归一化互信息
在配准的过程中,可能会受到两个图象的交叠处的面积大小的影响
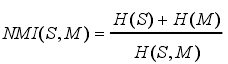
5.7 均方误差和
表示两个对应点的误差的平方和
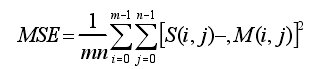
5.8 相关系数(CC)
从量化的角度出发,评价图像的相关性,下述图像的S、M表示的是两个图像的密度
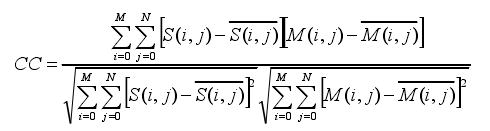
06
第六章、搜索策略
【优化算法】
详情可参见本篇文章:
优化算法综述https://zhuanlan.zhihu.com/p/272656135
07
第七章、灰度插值方法
在变换的过程中,浮动图像的像素点不会落在网格上,需要一个插值方法,近似o 到整点坐标上,这样的话才会有相同的分辨率。
解释:利用周围区域的若干网格点的灰度值来估计网格的灰度。
分类:最近邻插值、线性邻插值、三次卷积领插值、基于小波的插值、基于边缘信息的插值。
最近领插值:
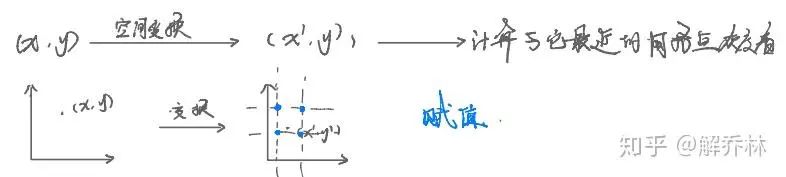
线性领插值:

解释:就是插值点的四个区域点的水平/竖直的权重(距离)
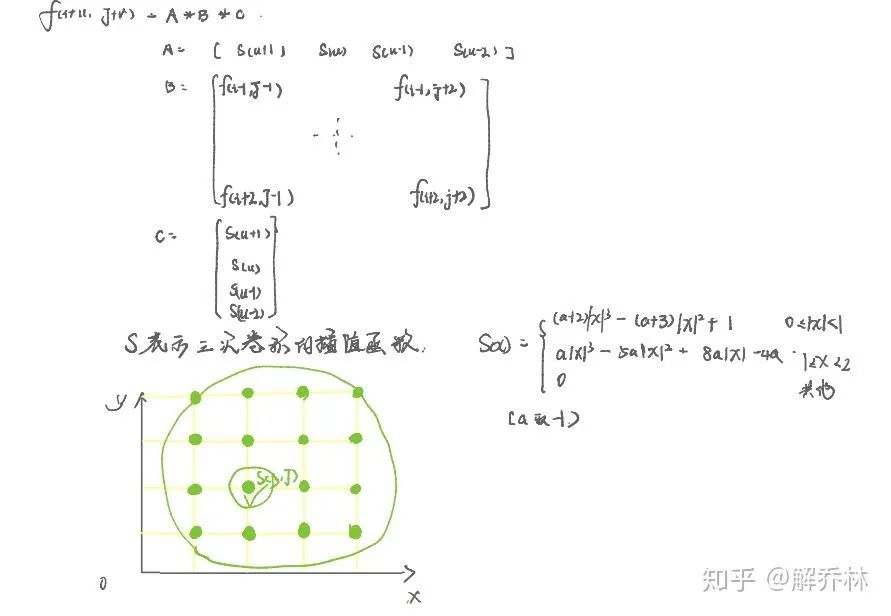
三次卷积领插值:
利用附近的十六个点的灰度值按照一点的加权(距离)来估计这个点的灰度值!
08
第八章、医学图像配准的评价
难以取得N全其美的情况下,只能做到最优化配准
8 判断指标:准确性、时效性、鲁棒性以及可靠性
准确性:判断是否准确配准(最小均方误差、峰值信噪比、相关系数、互信息、归一化互信息等)
时效性:时间
鲁棒性:在不同模态、噪声、参数等条件下,是否还能够准确的配准
可靠性:多次配准下的平均程度
8.1 可视化
直接:就是将参考图像以及浮动图像放在同一参考框架下
单点:识别参考图像上的每个目标点在浮动图像上的目标点
多点:多于两点的对应位置
8.2 当误差小的时候
精确度:先对病人进行基准标定法对病人进行原始数据的收集,作为一个标准。然后回顾性算法对其配准,利用欧几里得距离作为其目标标准误差(TRE),利用它来衡量其精确度,基准配准误差(FRE)及其基准定位误差(FLE)佐以辅助。
成功性:就是可重复性,下次再按照其方法做的时候的成功率。
执行时间:配准时间的执行效率 。
鲁棒性:其稳定性如何?利用其噪声免疫、图像灰度、形变大小衡量。
09
第九章、主要的配准方法
9.1 以特征的方法分类
1)点法(内部点&外部点)
内部点从病人相关的性质得到的,比如解刨标志点,在三维空间定义。必须可见。血管的分叉或者交叉处等。
外部点:外加附加标记物:比如在皮肤上做上标记物等方法。
评价:外部点比内部点好识别,但是受试者必须保持不动等外界因素会影响。内部点比较友好但是寻找麻烦而且带有主观性。
2)曲线法
人工在投影图像中找开曲线-局部曲率最佳拟合的线段用相同的采样率找出对应点,然后再用点法配准。
3)表面法
"头帽法",一幅图像中提取点集-帽子,另一幅图像(分辨率较高的图像)中提取表面-头。
4)矩和主轴法
计算两个图像的像素点的质心以及主轴。通过平移旋转使得两个图象对齐。但是这个方法对图像缺失较为敏感,必须完全的出现在整个图像中。
5)相关法
原理:利用图像的相似性最大化的原理实现图像的配准-优化相似准则进而估计变换参数
问题:这个时候必须做到的是尺度变换以及曝光时间不同引发的强度差异的不同
具体技术:相关函数、相关系数、插值平方和、差值绝对值和等
优化:但是计算非常的大,现有几个方法:相位相关傅里叶估算平移旋转参数、遗传算法、模拟退火法等优化等
局限性:主要利用的是单模态图像的配准
6)最大互信息配准法
如果两个函数对其的话,对应的体素的强度值的互信息最大。不用对强度关系作为假设,不用做图像分割等。对任何甚至残缺的图像也是可以起到一个很好的配准效果
7)图谱法
比如人脑,每个人的的解刨结构等还是具有一定共性的,我们构造一个解刨图谱,进行配准,就可以利用人们的先验知识进行自动的识别配准。
9.2 以配准方法分类
1)刚体配准的发展
1、外部特征点法:人工加入特征点,比较其配准图像。简单、快、相对准确、容易实现自动化。但是给患者带来了极大的不适,而且需要手工标记、难以回溯。
2、内部特征点配准:解刨结构点(比如血管的交叉点、骨骼的拐点)、几何特征点(角点、曲率点、直线段、边缘、轮廓等)、统计特征点(重心、质心)、像素强度特征。它能够带来回溯性,而且不会对患者造成危害。但是需要交互啊,难以实现完全的自动化。
3、基于分割的配准:在控制点配准的基础上,基于分割的配准。
头帽法--距离平方和最小来确定变换关系
快速斜面匹配算法---通过距离变换的方式去配准解刨二进制图像
分割直线的方法配准
轮廓的配准方法---拉普拉斯-高斯方法去配准轮廓,链码表示轮廓,确定变换
等
但是分割是半自动的,难以实现全自动。而且受分割的精度的影响
4、灰度配准
像素灰度作为另一个发展方向。
主轴和矩的方法:利用图像之间的像素灰度的统计关系进行配准。通过计算零阶以及一阶矩,得到质心与主轴,然后对齐。适用于多模态的配准。(基于轮廓-力矩的配准、基于正交矩的配准等),但是不是很准确,只能用于粗配准。
基于全部灰度图像的信息配准【依赖两幅图像的相似组织的灰度值是对应的假设】,计算对应像素对的统计关系进行配准图像。利用联合直方图描述相同组织区域的灰度的对应关系,利用其特点进行配准
熵配准---互信息
2)序列图像的配准发展
序列图像的用处:反映了病人的病灶的动态变化,进而来发现治疗的效果以及潜在的危险。
方法一、将图像进行阈值分割,即直方图分为4个区域。定义在不同区域的直方图计算值作为参数计算准则函数配准图像。---光滑、准确。
方法二、傅里叶变化的幅度谱进行极坐标重采样(旋转->平移),利用FFT变换,最后扩展到序列图像配准。
方法三、利用序列进行图像对应的特征点集进行三维刚体多幅图像的配准、迭代。
方法四、特征点的采集需要交互,所以利用像素强度,不需要用户的干预。---高阶互信息
3)非刚体图像配准的发展
因为人都有一定的弹性,对于非刚体、非线性变形时,弹性变换是非常重要的一种方法。
基于物理模型的配准方法:
连续的弹性模型
就是将两个图像看成物理过程。两种能量分布:一种是外部力量施加的外部能量,一种是内部力量施加的内部能量,当总的能量达到最小的时候,配准最好。通过有限元法、有限差分法等求解偏微分方程进行i非刚体的变换。
应用弹性模型
外力作用下的位移量进行梯度运算和拉普拉斯运算得到变形体在外部作用下的产生的内部变形能量。
粘性流体模型
就是将浮动图像当成粘性流体,内力作用下,流动进而达到配准,内力随着变形不断地释放。
光流配准
在CV中,物质的运动一般是用图像灰度的分布体现的---光流场。光流场反映了图像运动的速度,就是不同图像之间的最佳拟合的位移。
基于物理的模型适用于大变形,适用于不同图像、图像与图谱之间的配准。
弹和粘不能模拟高度的局部变形,具有局限性。
基于偏微分的求解并不能求出最优解,只能不断地迭代求解。
9.3 基于参数的空间配准
参数化的非刚体变化拟合参数之间的非刚体变换
1)基于多项式的非刚体变换
仿射变换(9个自由度)、二项式的变换模型(30个自由度)、三次、四次等等;全自动的图像配准算法最高为五次。描述图像的非刚性变化,他只能模拟不能调整。
2)基于样条函数的变换
可以模拟图像之间的局部变形。参数化的样条计算,可以模拟所有刚体、非刚体、仿射运算,简单。
其中B样条最为广泛。假设一个弹性样条被嵌入到图像中,移动样条控制点来改变目标表面形状。
插值样条:图片中近似的特征点,根据位置对整个图像用薄板样条插值函数计算非刚体变换,然后寻找相似性的极值,实现非刚性变换
基于B样条的医学图像快速弹性配准:分块计算,部分更新。
3)径向基函数的参数化变形
它既可以模拟全局、也可以模拟局部非刚性形变。被广泛应用于非刚性的图像配准中。
通过一系列径向对称函数的线性组合来实现。一开始用于插值不规律曲面。径他所描述的曲面上的点的位置只与控制点的距离有关。
9.4 基于多分辨率分析的图形配准
他是为了加快优化收敛速度、避免陷入局部极值而发展起来的。图像太大,导致耗费大量的时间以及容易陷入局部最优点。因此,应用多分辨率分层配准。随着分辨率的降低,细节会被掩去。这个时候低分辨率快速配准,高分辨率因为初始值非常好,使得配准速度更快。这就是多分辨率配准。
高斯金字塔
拉普拉斯金字塔
小波多分辨率分析:确定小波分解的层数以及高通低通滤波器的系数,利用卷积确定多分辨率分析后的小波系数:一开始是从傅里叶分析而来,通过卷积实现,但是因为计算复杂、运算速度慢、对内存的需求大,不利于重构。
综上:外部特征-内部特征;单模态-多模态;二维图像-三维图像;刚性-非刚性;
10
第十章、基于信息论的医学图像配准【互信息配准模型】
一开始,信息论是专门研究信息的有效处理以及可靠传输的一门科学。香农首次对信息论建立了数学模型,现在,信息论已经渗透到图像处理中,本小结就是研究互信息在医学图像配准中 的应用。并描述了几种关于信息论的处理方法。
互信息的值并不是一个闭区间,优化函数多峰,容易陷入局部最优点。
10 信息论基础概念
1) 熵是什么?
熵是表示分子的混乱程度。越是混乱,熵越大。一开始熵是来源于物理学,后被香农量化到信息论中,表示信源的不确定程度。一般利用灰度直方图来统计像素灰度值的概率分布情况。
2)香农熵:
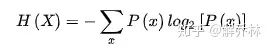
(X表示离散的随机变量,p(x)表示离散的随机函数)
例子:
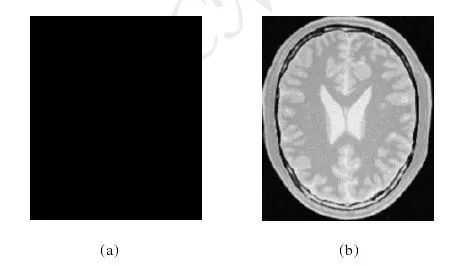
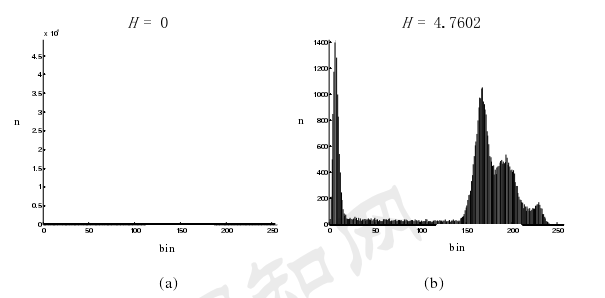
如上图:灰度级别越分散,灰度越分散,熵越大。
香农熵的性质:非负、凸、对称、具有极值性.
3) 联合熵和条件熵
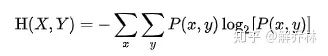
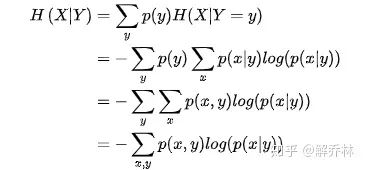
注:如果把熵的概念扩展到一对随机变量中,他是衡量一对随机变量所包含的信息量,换句话说就是这两个变量的相似程度。
4) 条件熵、边缘熵、联合熵之间的关系
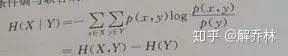
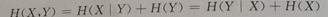
例子:下面的图b-e是原始图像旋转10、20、30的联合灰度直方图分布

越不匹配,对应的联合灰度直方图越复杂。
5) 相对熵与互信息
互信息通常用来描述两个图像之间的统计相相关性,通常用I表示;
相对熵表示的是两个随机变量间距离的一种度量D,而互信息表示的是一对随机变量包含另一个随机变量之间的程度I,当两个实际变量相等时,D=0,I=1,公式如下:
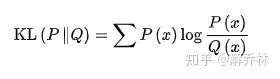
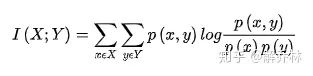
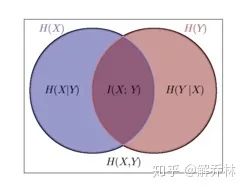
互信息与边缘熵、条件熵、联合熵之间的关系
10.2 互信息在图像配准中的应用
不同模态的图像,他的相同目标的灰度可能不同,但是他的组织、器官,灰度值对应的三维空间相同位置是相同的-统计相关的。把互信息作为配准测度,两幅图像配准最好时,互信息达到最大。
1)图像互信息【只有将图片灰度转化为概率密度时,才可以用其目标公式】
如果把图像的灰度值作为随机变量,引入互信息,这个时候,我们就可以利用其定理衡量图像。
步骤:
图像的边缘概率-利用直方图估计
图像的联合概率-利用联合直方图估计
概率分布估计
参数估计(假设每一类概率密度已知,参数未知,这个时候利用贝叶斯、最大似然估计);
非参数估计:利用直方图、核密度、K临近。
2)概率密度估计【只有将图片灰度转化为概率密度时,才可以用其目标公式】
直方图估计(快、简单;但是只能估计离散的分布)
核密度估计(能估计连续概率分布,用于非刚性配准)
1、直方图估计:
简单来说就是参考图像与浮动图像,各自关于灰度划分n,m个区间,统计每个点的灰度落在那个区间,通过它可以了解到各个点的灰度情况以及分布是否均匀或者分布在那个区间内。
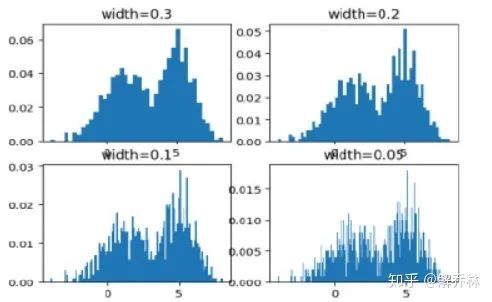
但是直方图估计会导致信息的丢失,并且他不是唯一的,也不是平滑的,而且无极值
2、核密度估计(帕曾窗估计)的原理:
利用核密度对样本进行平滑,使得得到连续的概率密度函数。
他是基于样本平滑的、样本来估计总体概率密度函数(核密度估计其实是对直方图的一个自然拓展。)
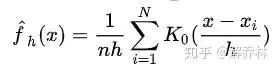
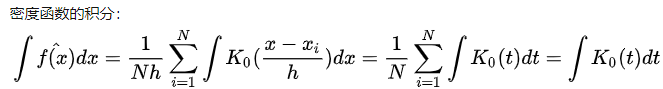
通过上面公式,大家也能看出,其实核密度估计就是对直方图的一个扩展,或者说是平滑,他的要求只有一个,就是这个函数的积分为1。
书上提到了4种常用的核密度函数:
矩函数,三角核函数,高斯核函数以及一二三阶B样条函数


注:B样条它能够很好的用于用于非刚性配准
10.3 基于互信息的医学图像配准
核心:将互信息作为衡量待配准图像的相似度
首先:图像配准可以看成是寻找两个图片的最优空间变换的过程。
算法公式化【目标函数】
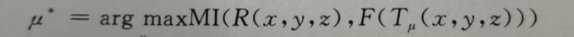
注:argmax表示的是当μ取到何值时,使得后面的式子最大,MI()表示参考图像与浮动图像之间的互信息,R(x,y,z)表示参考图像,F(Tμ(x,y,z))表示浮动图像,这个Tμ表示对x,y,z的转换,如果不是整数,一般是用插值()的方法
10.4 具体化配准算法流程:
1)空间变换【搜索空间】--FFD
根据前面的基础知识可知,空间变换分为:刚性变换、仿射变换投影变换,弯曲变换(弹性形变)弯曲变换-自由形态形变(FFD)+B样条函数性能较好。
基于B样条的,自由形态形变模型用于建模图像间的局部形变是非常好的。
步骤:
1、为了提高效率,先用全局变换对图像进行粗配准
2、变:Tμ,利用网格以及三阶B样条(平滑)的线性结合
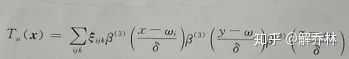
上面的 ξ 表示网格与控制点的控制矢量, ω 表示各个方向上的控制点, δ 表示网格的间隔。这个时候,我们就可以通过网格法以及三阶B样条(用于平滑),进行配准了
2)配准模型的求解(增量与方向)【搜索策略】--L-BFGS
我们需要优化算法求出下述目标函数的极值
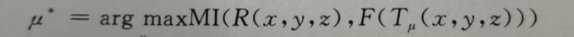
根据上述优化算法的介绍,我们发现牛顿法比梯度法更好的收敛,但是牛顿法要求海森矩阵的逆,非常的复杂,提出了伪牛顿法BFGS,我们自己更改,L-BFGS为伪牛顿法的变种(就是在有限的空间内的BFGS)
泰勒公式:
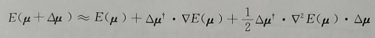
Δ μ表示其增量,进行迭代
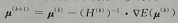
迭代过程,H表示每一步的步长,是海森矩阵逆的估计
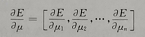
n表示空间变换的参数的个数,刚性全局变换,参数为6个,非刚性变换,参数是看网格的大小。
3)【相似性度量】--互信息
1、概率密度估计(互信息以及相似度度量的基础)
为了保证概率的鲁棒性,需要计算相似度的解析导数,通过核函数估计连续的概率密度函数【直方图估计是只能估计离散的核函数】
一般用0阶B样条函数来估计参考图像的概率密度函数
参考图像的概率密度函数:
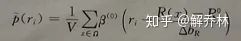
浮动图像的概率密度函数:
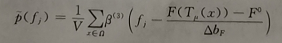
联合密度函数:
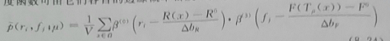
条件密度函数:

注:R°,F°表示图像的灰度的最小值, Δ b表示箱宽。
他的值代表着参考图像和浮动图像之间的差距==灰度差距
2、互信息求导(求其精确度)【相似性度量】--互信息
这个时候,我们把前面的概率密度函数等全部带入到
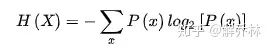
后,对其求极值,就能够得到μ何时时,下面的目标函数最大了
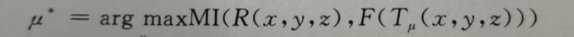
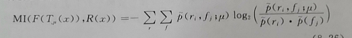
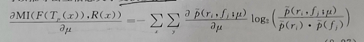
对其求导:
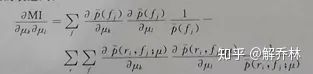

这样,我们就完成了任务。我们来梳理一下算法流程:
互信息并不是直接的对图像的灰度值进行衡量其一致性,而是量化待配准图形的概率分布之间的相关性,使用优化的方法使得图像的互信息达到最大值的空间变换,是指精确配准。
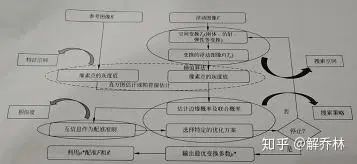
解析流程:
针对目标函数的求解过程
首先,对浮动图像通过空间变换,变为F(Tμ)【搜索空间】,利用差值算法,得到浮动图像的灰度值,对参考图像进行灰度值计算,通过直方图或者帕曾窗估计对参考图形、浮动图像的像素点的灰度值进行估计。【特征空间】,对浮动图像估计边缘密度、联合密度,与参考图像进行互信息配准,选定优化方案【相似度度量】,当达到一定的步数,或者μ的临近两次差值足够的小的时候,输出最优变换μ【搜索策略】,并且利用μ※对参考图像以及浮动图像进行配准。
10.5 几种基于信息论的相似性度量方法【对香农熵的一种优化】
归一化度量【NMI】(解决了互信息对图像重叠问题的敏感度问题)
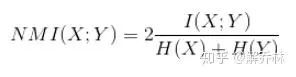
熵相关度量【ECC】(类似于归一化)
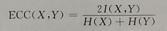
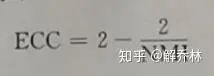
互累计剩余熵【CCRE】(具有更广泛的性质,将概率分布转化为累计概率分布问题)
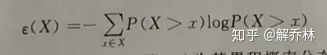
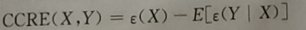
Alpha互信息【A-MI】(推广)
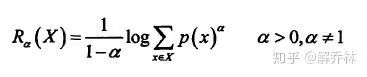
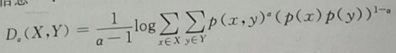
詹森瑞利散度【JRD】(互信息的另外一种形式,利用詹森不等式和香农熵构造的一种散度)
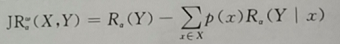
11
第十一章、基于Jensen-Arimoto散度的医学图像配准【香农熵、互信息的优化】
介绍:
基于图像特征的配准取决于对特征的提取与选择,可能会出现对比度低、噪声影响大的问题。
基于灰度的配准又分两种:
一种为灰度的差异作为配准的标准(SAD、SSD:适合单模态的配准)
一种为利用图像之间的概率作为相似性度量(信息论)---互信息(基于香农熵)
J-A:香农熵的变种,因为香农熵并没有考虑两个独立随机变量的相互作用,引入了伪可加的Tsallis进行精确配准。精确配准而且适用于多模态。
11.1 Arimoto熵
离散随机变量X,他的概率分布:p=(p1,p2,p3...),则:
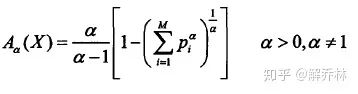
这个时候,当a趋近于1的时候,A熵就等于香农熵
1)具有的性质:
非负性,伪可加性,凸性,对称性,有极值
针对伪可加性得:
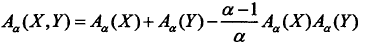
这个就是对香农熵得的最大的改进。
针对极值性得:
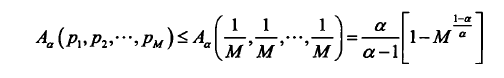
当每个概率相同时,他的A熵最大。
2)对α的讨论:α的值不同,A熵的曲线不同,如图:
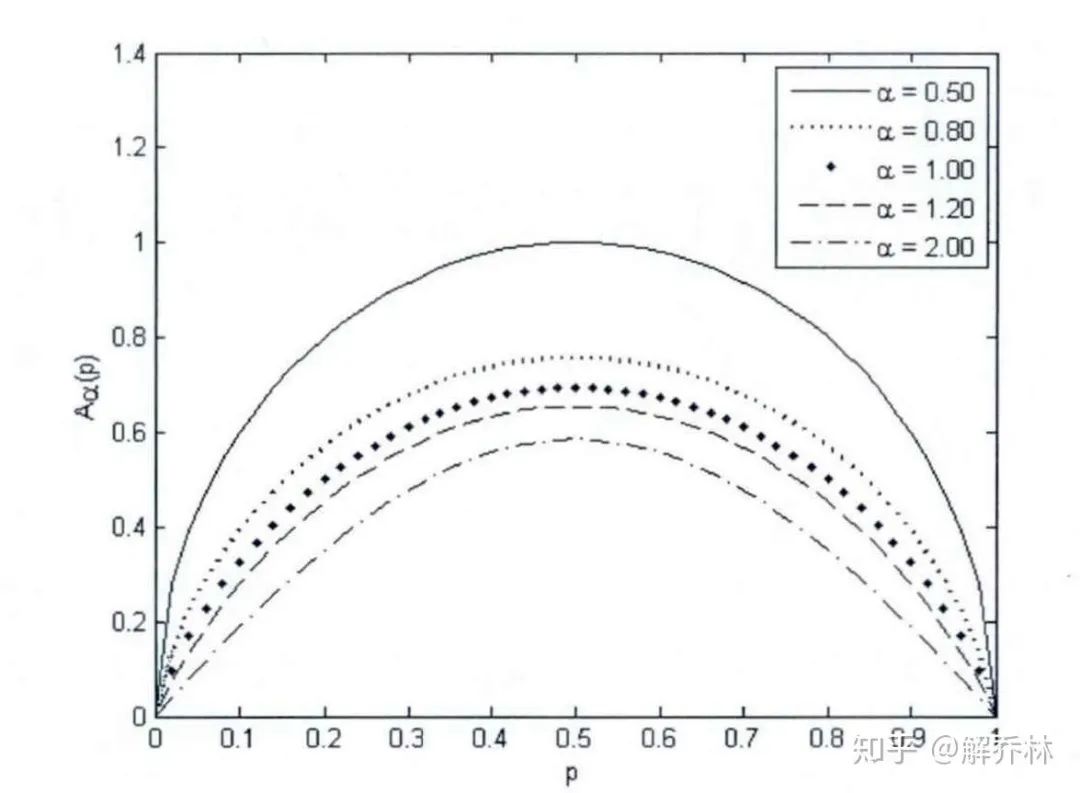
中间那条虚线,表示a=1时的A熵,也叫香农熵
A熵随着a的增大而减小
3)J-A散度
J-香农结合A,提出了一个新的散度测量,JAD,它也可以量化随机变量概率分布之间的距离。
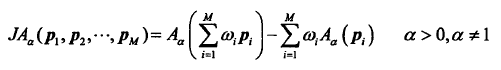
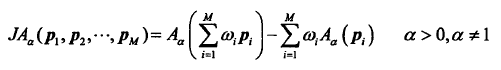
注:w表示加权因子,p表示关于X的随机变量的概率分布
它是一个凹函数。
4)JAD与现有的信息论测量的联系【A-MI、Tsallis熵】
A-MI熵:
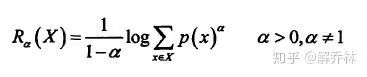
关系:
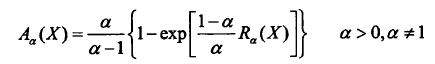
TE熵
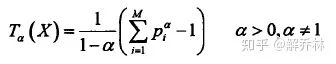
关系:
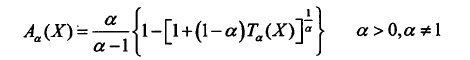
基于上面的形式,给出了JRD与JTD两种散度
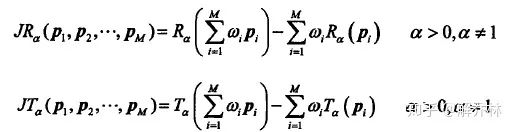
将之带入到JAD中,可得关系:
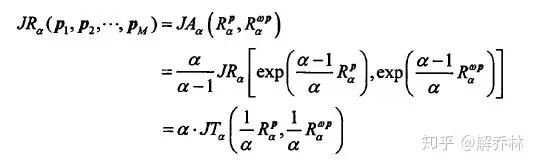
说明他们具有相同的性质,当a->1,都为JSD
11.2 基于JA的散度医学图像配准算法
本小节详细的描述了,基于JAD算法的图像配准全过程。
配准类型->空间变换模型->用JAD作为相似度度量+基于梯度的优化算法->配准。
步骤:
1)配准框架
参考图像R,浮动图像F;
浮动图像空间变换(刚体、仿射等)使得
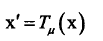
公式化问题,获得目标函数。他们之间的配准可以看作下面目标公式的优化问题
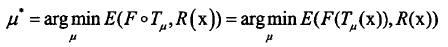
°表示浮动图像
2)变换模型--FFD
空间变换模型就是在一开始用什么进行两个图像的配准,供我们选择的有刚体、仿射、投影、弯曲变换。这个时候,我们一般选用刚体进行粗配准,选择弹性形变【FFD:自由形态形变】用于精准的配准。
同时发现选用B样条去模拟平滑控制有很大的优势。
综上,我们选用基于B样条平滑的FFD模型进行局部形变。
针对三维形变,一般通过三阶B样条进行形变,公式如下:
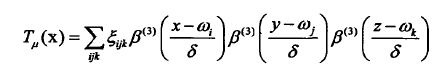
w表示x,y,z方向的控制点,E表示形变系数变量
3)目标函数【相似性度量】--JAD
将相似性度量转化为相异性度量
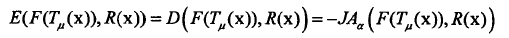
代入目标函数:
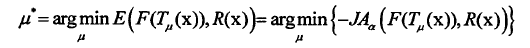
注:箱子数:M;灰度级:f,r;【利用核函数或者直方图计算图像的概率分布】且:
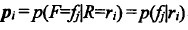
用参考图像的概率分布作为加权因子:
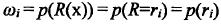
带入到JAD中,
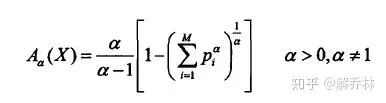
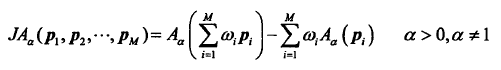
得:【代入方程还没弄清】
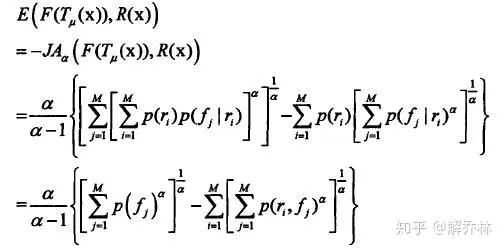
通常,配准图像只需要一个相异性度量就可以了,但是,不同的是,JAD方法中,我们引入了一个平滑项,即惩罚项,用于约束图像的局部形变。惩罚项如下:
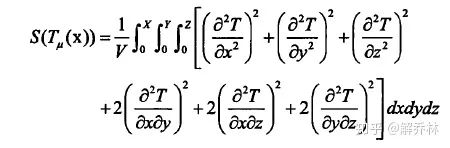
这个时候目标函数:
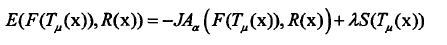
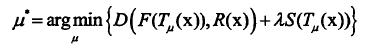
4)优化方案--L-BFGS
上面也说过,因为准确率、收敛、Hessian矩阵计算量的问题,梯度下降法、牛顿法等的缺点,我们用的是L-BFGS方法,对其寻找目标函数的最小值。
泰勒展开式:【保留前三项】
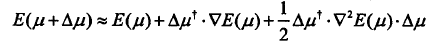
迭代:
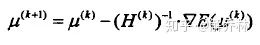
这里的表示海森矩阵的逆的估计
求导:
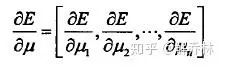
n表示参数的多少
具体运算:
概率密度估计:
基于B样条的R(x)的概率密度函数
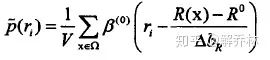
基于B样条的F(Tμ(x))的概率密度函数:
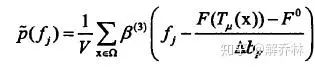
联合概率密度函数表达式:
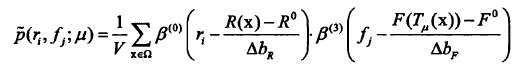
由上可知:条件概率:
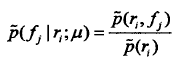
目标函数求导
相异性度量D与平滑项S
S:
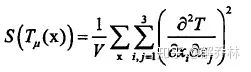
S的导数:
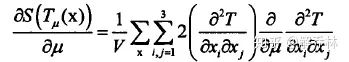
D关于μ的导数:
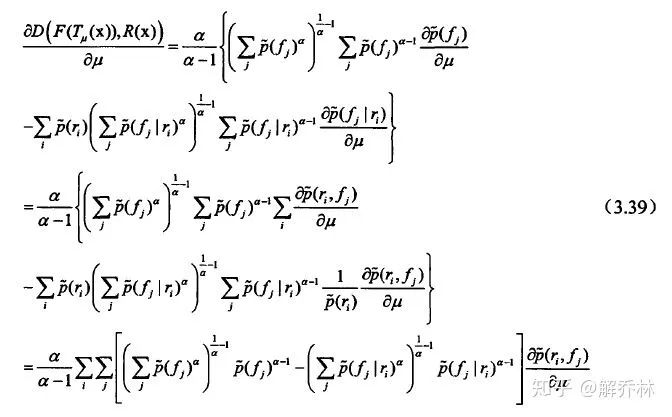
关于
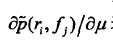
得
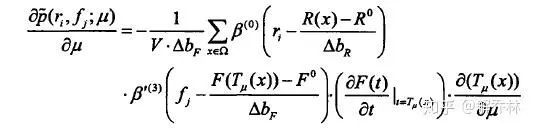
设置停止项:
当达到设定的步数或者每一次的增值小到设定的值时,停止。
11.3 算法比较以及实验结果分析
书中这一小结是为了比较JAD得医学配准的性能,分别从非延展重叠性、精确度、灰度不均匀性、重叠及其收敛范围进行比较。
1)参考图像与浮动图像的获得
1、三维脑部MR图像:T1、T2、PD加权。----金标准
2、真实的脑部图像:MR、CT、PET
非延展性说明:
为了说明JAD的为可加性对图像配准的优化影响,我们利用JAD与互信息来配准MRT1的图像。
首先我们知道了金标准图,但是并不知道浮动图像,先用某种公式去将金标准变为不同浮动图像,然后再配准,然后再比较。

这个是我们的形变的公式,m代表形变量的大小,6组的形变系数出现六个图像,如下:
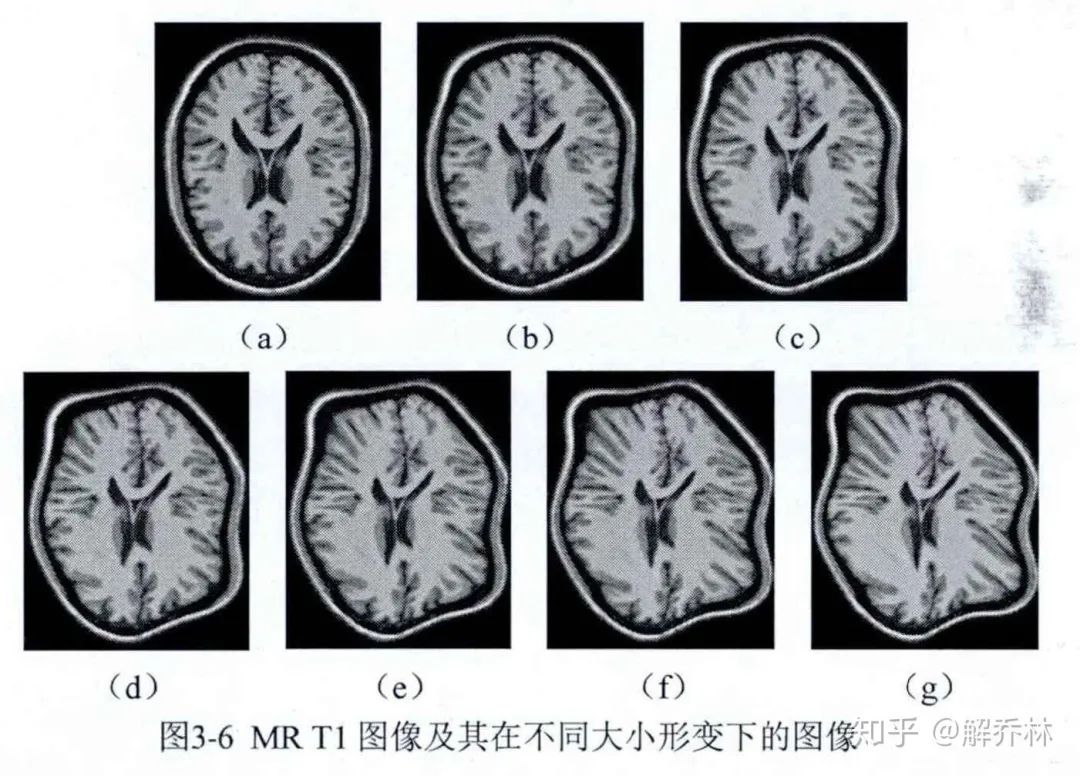
这个时候,我们把a作为参考图像,其他的作为浮动图像,利用JAD与MI对其进行配准,看一下其配准的效果,就可以知道谁更适合了。
最后的结果当然是JAD在a=1.5时效果更好。
上述旨在告诉我们,如果没有数据,应该怎么获取数据。
11.4 仿真配准实验
1)刚性配准
步骤:
参考图像&(参考图像+刚性配准)浮动图像【刚性变换的平移量以及随机角度为-40-40】
采取JAD、CCRE、NMI执行
针对误差:JAD能获得较小的误差
引入高斯噪声,引入标准差在0,10,15,20,25,加入MRPD图像中,进行配准,JAD更加的精确
让参考图像以(10mm,8°)的均值,(2mm,2°)的标准差的正态分布进行了随即变换。-------浮动图像->配准(针对3个旋转角度与3个平移量)--------------JAD、NMI较好
灰度不确定性:采用二次非均匀的将原始图像转发为浮动图像,下为二次非均匀因子;JAD好用
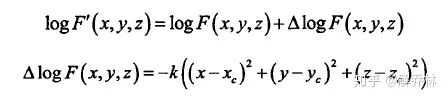
K为尺度因子,xc,yc,zc为非均匀展开的的中心点的坐标
3.5、我们通过截断原始图像来模拟图像间的部分重叠。
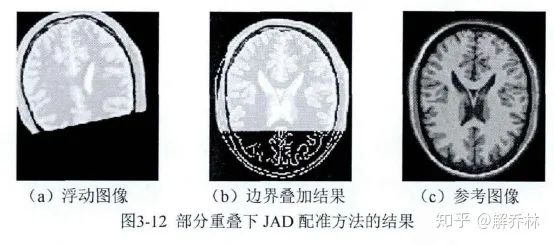
收敛范围:收敛范围【像某一个范围靠近】是衡量相似度优劣的重要指标,当收敛范围越大时,精确度其实是越小的。实验得JAD是具有在较大的收敛范围有较高的准确率的。
2)非刚性配准
参数设置:非刚性配准最重要的就是参数的设置,一般是试错法进行设置。
要学习的参数:JAD的非延展参数 α 、箱子数M、网格点 δ 以及随机抽样点的数N、
1、精确度:选60个m值
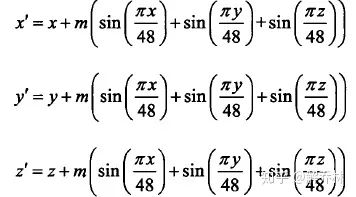
根据上述公式进行形变,有60个浮动图像

配准发现,JAD比MI更好
2、噪声:确定m,然后加入60个不同水平的高斯噪声,这个时候配准,发现JAD好
11.5 小结
香农熵的不足(独立之间的相关)
新的信息论相似度—>JAD<—Arimoto概念出发
JAD的性质->JAD与其他信息论相似度的关系——>新的配准方案(刚&自由形变)+弯曲能量惩罚+L-BFGS算法->窗函数估计边缘及其联合概率密度——>计算相异性度量D+平滑项S的导数----->解析导数
最后:仿真数据及临床实验测试其JAD的配准效果。
12
第十二章、估计待配准图像方法概率密度
12.1 概述
信息论主要应用于多模态的医学图像配准中,它有一个必不可少的步骤就是估计待配准图像的联合概率。
获取联合概率的方法:
直方图估计【简单,但是它受制于箱子的数目,而且图像是离散的】
帕曾窗方法:概率密度的估计【有很多的核密度,不知道选用哪一个更好,而且高维度会出现拖尾现象】
非参数窗(NP)【精度高但是计算量大】--平面插值的方法减少了他的计算量
注:标准直方图和帕曾窗都是把图像看成像素的一个集合
离散直方图转换(DHT)【对多变量直方图的一个平均,这样的话可以缓解箱子边界的不连续性】【但是随着箱子的增大,计算量越来越大】【利用多变量频域多边形MFP来降低DHT的计算量,但是他们同样是依赖箱子的数目】
部分体积估计(PVE)【通过非网格点到附近网格点(4、8个)的距离来计算权重进而更新其直方图】
广义的部分体积估计(GPVE)【仍需要直方图与核函数】
连续图像表示(CIR)计算待配准图像间的联合直方图【与PVE一样利用图像的连续表示。但不受核函数影响】
快速连续直方图估计FCHE【降低图像配准中的网格效应,减少大尺寸的配准时间,抽取样本来进行估计。精确度+执行效率】
利用估计图像的联合概率-计算信息论的相似度-单纯性优化方法求目标函数的最小值-评估其效果
12.2 基于连续图像表示的直方图估计
1)部分体积估计(PVE)【面积】
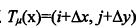
浮动图像和参考图像点的关系
这个点把整个小方格分为了4个部分,
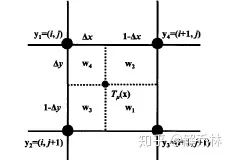
更新直方图:
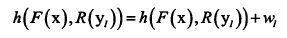
2)广义部分体积估计(GPVE):【将PVE进行广义化】
利用一个三角形函数进行推广,当然也可以用B样条函数等等来代替
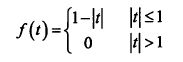
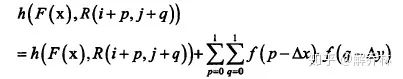
二维
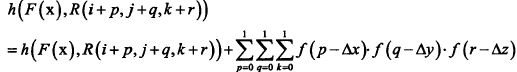
三维
3)二维图像联合直方图CIR
二维图像的灰度是一个连续标量函数:
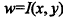
假设图像视野中服从均匀分布的位置随机变量:
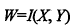
这个时候,就表示w表示在x,y点的灰度值。如果我们定一个灰度值β,则W的灰度值在β的累积分布就等于其面积之比。(换句话说,就是灰度值小于某一值的区域等于其面积之比)
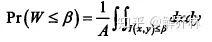
A为面积
再换句话说:A像素点的集合/总像素点的集合=A面积/总面积
注:β表示的是灰度水平曲线!也表示灰度值,因为定义的是连续均匀灰度图像
则概率密度为:
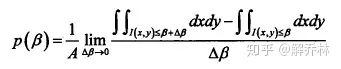
即:
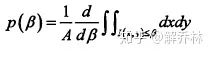
这个时候再引入X=u(x,y),Y=I(x,y);u、I表示的是平行或者垂直于灰度曲线β的方向【看不懂!】
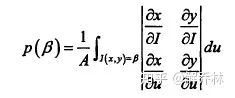
即:
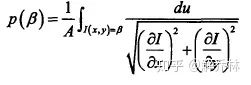
边缘密度估计
注:发现,给定灰度水平曲线,上面的点对应的灰度值的概率密度与该点的梯度的模成反比
推广到联合密度:
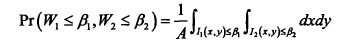
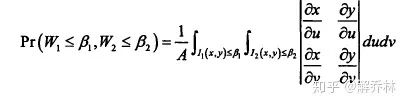
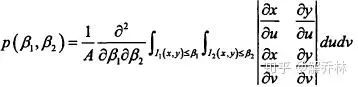
可能不存在,上面的那个式子不一定可导
利用几何的形式来求解其联合概率:
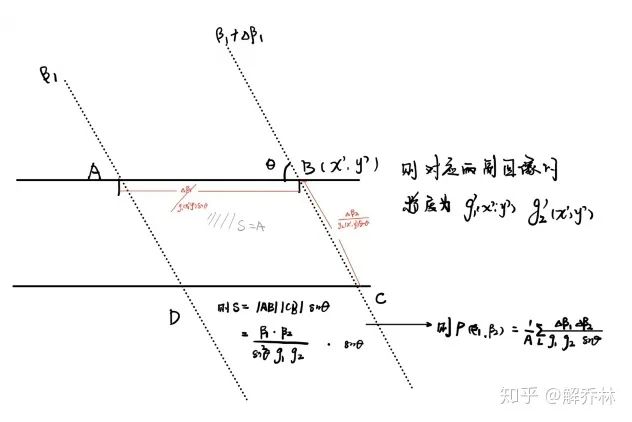
4)三维图像联合直方图【一一与二维对应】
与二维类似,三维边缘密度表示为:
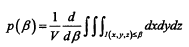
代换:
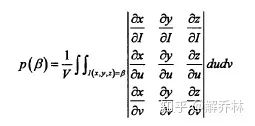
表达:
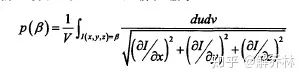
联合密度为:
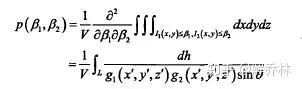
12.3 随机抽样理论【简化计算量】
联合直方图需要图像的样本来估计,但是样本太大计算量太大
利用抽样的方法会降低计算量
只选取那些明显特征的像素点作为样本【提取图像中的边缘信息】
均匀网格抽样
随机抽样(像素点随机抽样与非像素点随机抽样)
非像素点抽样--霍尔顿抽样
遵循伪随机霍尔顿序列,具有低差异性质
什么是低差异性质?
如3000个像素点随机分布,但是通过随机发现,这些点并不是均匀分布的,聚群现象非常的明显
N维空间大小为M的点集的均匀质量被叫做“差异性”,表示为:
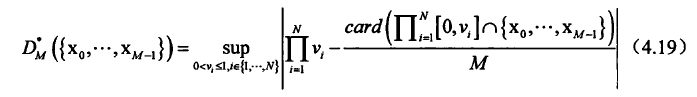
略
12.4 快速连续的直方图估计【估计概率】
在第二小结中,介绍了基于连续图像表示的直方图估计方法,但是仍需要利用核函数。
基于面积的直方图估计方法以及基于体积的三维图像直方图估计方法会耗费大量的时间。
我们介绍另外一种估计方法:
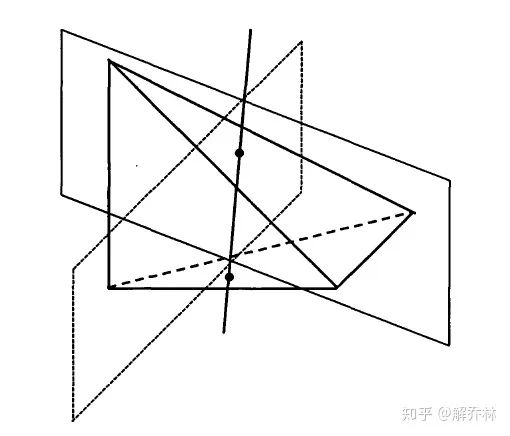
1)二维图像的FCHE
就是找一个正方形,对折变成了一个三角形,有已知的三个点的灰度值,构建函数
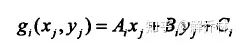
解得ABC,这个时候,如果两幅图像的灰度值
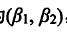
代入方程
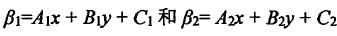
换算后的关于XY的两条直线,如果落在三角形内,则更新直方图。
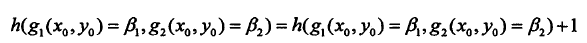
三角形:
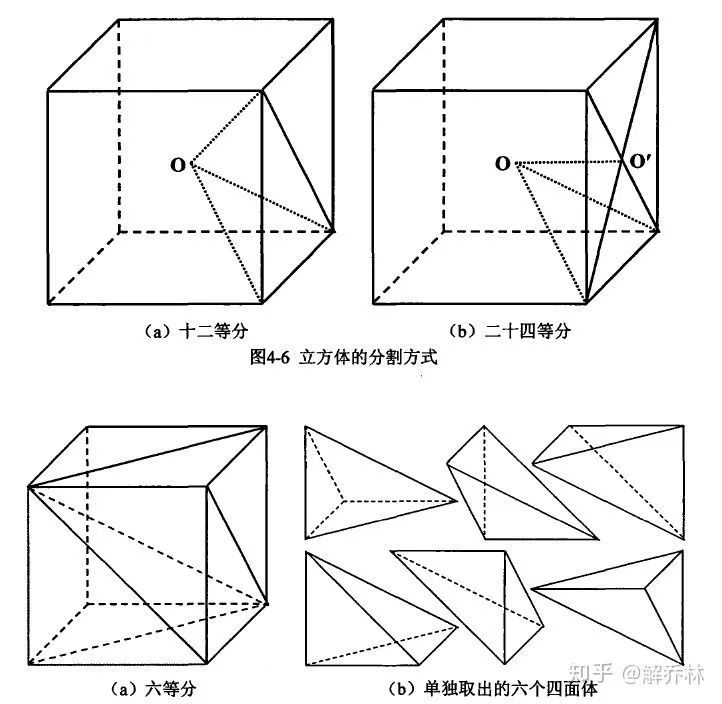
三维图像的额FCHE
同理;就是计算复杂一点而已
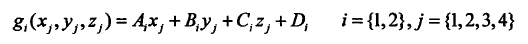
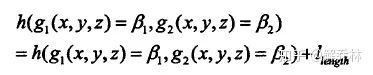
12.5 基于快速连续直方图的医学图像配准
步骤:空间变换模型->构建目标函数->采用优化方案求目标函数的解
1)空间变化模型
利用刚性变换模型对其进行配准(连续的直方图估计并不适用于形变配准)
2)目标函数
基于Arimoto熵作为衡量其形式度的函数,并不需要平滑项。其目标函数仅包括相异性度量
由此,目标函数为:
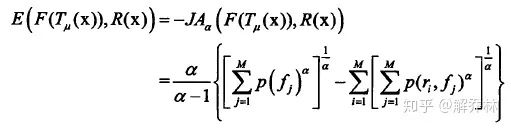
p(f),p(r,f);一个表示其边缘概率,一个表示其联合概率分布
由上述可知,要想计算其目标函数,必不可少的是求其边缘概率以及联合概率分布。我们采用FCHE方法进行估计两概率的分布
3)优化方案
FCHE并不能获得目标函数的解析函数,所以我们不能用梯度下降的优化算法。--单纯形方法并不需要计算目标函数的优化方法(NM)
注:单纯形方法就是一个迭代求最优解的问题。隶属于线性规划的问题。
采取逐步接近最优解的办法,先求出一个可行解,但它未必是最优者,然后逐步改善可行解,使目标函数值逐步增大(或减小),直到目标函数达到极值(最大值或最小值)时,该问题就得到了最优解,或判断无最优解。
换句话说就是,用单纯形的方法,代替牛顿法、梯度法等,进行迭代求解最优解。
12.6 小结
提出了基于连续图像表示直方图的估计方法-----快速连续直方图估计。
介绍了传统的直方图估计的不足(离散、受限制于箱子的个数;计算量大;核密度的摆尾现象;)
介绍了几种连续抽样的直方图估计方法;【PVE、GPVE、CIR、FCHE】
具体执行过程;【二维图像的联合直方图;三维图像的联合直方图】
4、描述图像的随机抽样理论,特别是非网格的随机抽样【霍尔顿随机抽样方法】
二维图像和三维图像的FCHE【快速联合直方图估计】
进行基于医学图像的配准【基于刚体变换、JAD相似度度量、NM(单纯形方法)(FCHE方法不能用,木有获得目标函数的函数)】
最后,用简单直方图、Parzen窗方法于FCHE比较
13
第十三章 基于熵图的医学图像配准
熵图在图像处理和特征聚类中,用处很大。他就是一个特征矢量的集合【熵用来确定一个系统的发散性、不确定性,或者随机性。】
熵特征相似度:首先,对熵图的的相似度的评估,就是类似于前面,对两幅图的相似度的度量。只不过以熵图为研究对象。下面是几个比较常见的方法。
13.1 a-MI瑞利熵
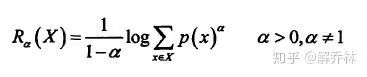
当a->0时,他就等于香农熵。
如图:相异性度量

这里:f,g表示的是两幅图像的概率
上述如果g=1时,也就是说图片均匀分布时
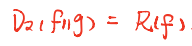
a表示散度,这里两个常用的散度:
黑林格散度(a=0.5)
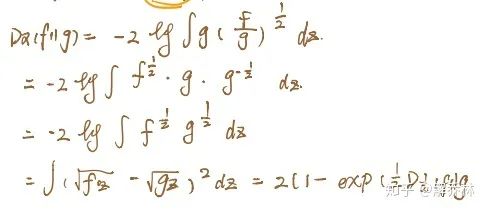
KL散度(a=1)
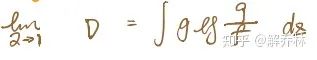
13.2 互信息和a-互信息
互信息和a-互信息,是衡量两幅图像的相似度的。【表示两幅图像相同的有多少】
首先,定义Z1,Zt,表示两幅图像相同位置的灰度值。然后引入概率分布,则F(Z1),F(Zt)、联合概率分布F(Z1,Zt)
如果:他们完全对其,则F(Z1,Zt)=F(Z1)*F(Zt)
这个时候,我们用a-互信息来衡量F(Z1,Zt)他们之间的关系,进而评判他们的相似度度量
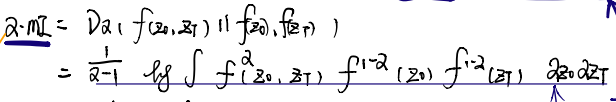
要记住,这些熵(香农熵、瑞利熵等本身就是一种工具而已,主要是来量化他熵,进而进行比较的一张人为的数学公式)

这个时候再引入误差的平均概率的问题,我们发现:

表示如果完全对立则H0,如果完全配准则H1
换句话说就是:权重之和为平均误差
a-詹森相异度度量
a-集合算术平均散度
14
第十四章 基于相关性的医学图像配准【概率论:相关系数】(NCC)
经典的相关系数
具有鲁棒性的系数中【选择合适的概率密度函数估计相关系数,提高鲁棒性】
估计随机变量的相关比【评价两个随机变量的相关程度】
条件相关比【空间信息扩展联合直方图+固定图像中小图像块灰度分布计算相关比】
增强相关系数定义,建立配准模型【前向叠加与反向组合的迭代方式对模型求解】
实验部分采用的是基于B样条的自由形态形变【空间变换模型】,基于L-BFGS算法,获取模型的最优解
14.1 经典的相关性
经典的相关系数是一种简单的,常见的度量,但是存在一个问题就是,他对外点特别敏感,什么叫外点呢?就是莫名其妙多出来的点。接下来介绍鲁棒相关系数的医学配准算法。
同样,用μ对浮动图像参数化,这个时候,得到目标函数:μ※=argmax S(F(Tμ(x)),R(x))
这个时候,因为x依赖于参数μ,我们得知:μ※=argmax S(F(μ),R)
由上可见,令F=X,R=Y,且X,Y是独立同分布的随机样本变量。
1)相关系数的估计
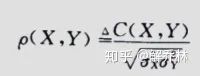
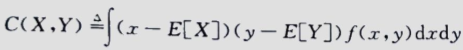
这个时候,如何估计相关系数是一个问题,后面给了两个估计相关系数的方法
一就是通过概率论中,样本相关系数:
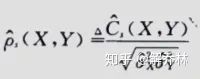
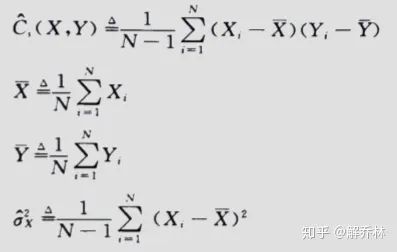
样本相关系数就是根据小的样本去估计总体样本,概率论中有详细介绍。
二就是用相关系数中的最大似然估计计算【略】
14.2 基于相关比的医学图像配准
就是浮动图像的灰度值=i,这个时候参考图像也必定有灰度值=i时,相对应的聚集。
我们可以借助这个,通过浮动图像灰度值去预测参考图像灰度值,反之。即功能依赖程度作为匹配准则。
步骤:
1、X通过 Φ (X)得到Y的最佳拟合
2、衡量拟合的程度
利用方差去衡量随机变量偏移平均值的程度
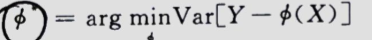

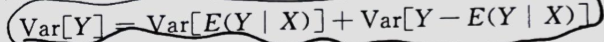
这个时候,相关比的定义就出来了:
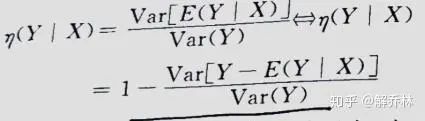
他是衡量X、Y之间的依赖程度。η∈(0,1)
问题是如何计算相关比?
离散:可以通过累加局部计算获得相关比。
连续:将其作为随机变量,确定其边缘和联合密度函数【二维直方图归一化、帕增窗估计】
14.3 条件相关比
条件相关比的优点在于:他能够利用空间信息扩展联合直方图,并且固定图像中,小图像块的灰度分布,并且计算相关比。【局部估计-局部配准】
14.4 增强相关系数的医学图像配准算法
他是图像对其问题的性能标准。具有光照扭曲不变性。
参考
[1]姚保琛,柏春松.基于特征的图像配准技术综述[J].现代计算机,2020(20):52-56.
[2]https://zhuanlan.zhihu.com/p/47649796
[3]https://www.zhihu.com/search?q=Harris%E8%A7%92%E7%82%B9&utm_content=search_history&type=content
[4]https://www.zhihu.com/search?type=content&q=SIFT%E7%89%B9%E5%BE%81%E7%82%B9
[5]https://zhuanlan.zhihu.com/p/70385018
[6]https://www.cnblogs.com/lzhu/p/8430355.html
[7]https://zhuanlan.zhihu.com/p/75538637
[8]https://zhuanlan.zhihu.com/p/75539207
[9]https://zhuanlan.zhihu.com/p/76543118
[10]https://zhuanlan.zhihu.com/p/76543118
[11]基于Demons算法【基于相关性的、搜索空间的配准】https://zhuanlan.zhihu.com/p/295369527
[12]基于图像特征的匹配https://zhuanlan.zhihu.com/p/328025577
编辑:黄飞
 电子发烧友App
电子发烧友App









































评论