什么是电阻的高频工作模式?
电阻器在高频场合中使用时,必须考虑电阻器固有电感和固有电容的影响。此时电阻器的等效电路相当于一个直流电阻Ro与分布电感LR串联,然后再与分布电容CR并联,如图所示。

一般情况下,非线绕电阻器的高频分布参数较小, LR为0.01 - 0.09μH , CR为0.1-5pF。线绕电阻器的高频分布参数较大, LR为几十微亨, CR为几十皮法。
电阻电桥的工作原理及其特性:
第一部分,主要论述了为什么要使用电阻电桥,电桥的基本配置,以及一些具有小信号输出的电桥,例如粘贴丝式或金属箔应变计。本篇应用笔记则侧重于高输出的硅应变计。本篇应用笔记作为第二部分,重点介绍高输出的硅应变计,以及它与高分辨率Σ-Δ模数转换器良好的适配性。举例说明了如何为给定的非补偿传感器计算所需ADC的分辨率和动态范围。本文演示了在构建一个简单的比例电路时,如何确定ADC和硅应变计的特性,并给出了一个采用电流驱动传感器的简化应用电路。
硅应变计的背景知识
硅应变计的优点在于高灵敏度。硅材料中的应力引起体电阻的变化。相比那些仅靠电阻的尺寸变化引起电阻变化的金属箔或粘贴丝式应变计,其输出通常要大一个数量级。这种硅应变计的输出信号大,可以与较廉价的电子器件配套使用。但是,这些小而脆的器件的安装和连线非常困难,并增加了成本,因而限制了它们在粘贴式应变计应用中的使用。然而,硅应变计却是MEMS (微机电结构)应用的最佳选择。利用MEMS,可将机械结构建立在硅片上,多个应变计可以作为机械构造的一部分一起制造。因此,MEMS工艺为整个设计问题提供了一个强大的、低成本的解决方案,而不需要单独处理每个应变计。
MEMS器件最常见的一个实例是硅压力传感器,它是从上个世纪七十年代开始流行的。这些压力传感器采用标准的半导体工艺和特殊的蚀刻技术制作而成。采用这种特殊的蚀刻技术,从晶圆片的背面选择性地除去一部分硅,从而生成由坚固的硅边框包围的、数以百计的方形薄片。而在晶片的正面,每一个小薄片的每个边上都制作了一个压敏电阻。用金属线把每个小薄片周边的四个电阻连接起来就形成一个全桥工作的惠斯登电桥。然后使用钻锯从晶片上锯下各个传感器。这时,传感器功能就完全具备了,但还需要配备压力端口和连接引线方可使用。这些小传感器便宜而且相对可靠。但也存在缺点。这些传感器受温度变化影响较大,而且初始偏移和灵敏度的偏差很大。
压力传感器实例
在此用一个压力传感器来举例说明。但所涉及的原理适用于任何使用相似类型的电桥作为传感器的系统。式1给出了一个原始的压力传感器的输出模型。式1中变量的幅值及其范围使VOUT在给定压力(P)下具有很宽的变化范围。不同传感器在同一温度下,或者同一传感器在不同温度下,其VOUT都有所不同。要提供一个一致的、有意义的输出,每个传感器都必须进行校正,以补偿器件之间的差异和温度漂移。长期以来都是使用模拟电路进行校准的。然而,现代电子学使得数字校准比模拟校准更具成本效益,而且数字校准的准确性也更好。利用一些模拟“窍门”,可以在不牺牲精度的前提下简化数字校准。
VOUT=VB×(P×S0×(1+S1×(T-T0))+U0+U1×(T-T0)) (式1)
式中,VOUT为电桥输出,VB是电桥的激励电压,P是所加的压力,T0是参考温度,S0是T0温度下的灵敏度,S1是灵敏度的温度系数(TCS),U0是在无压力时电桥在温度T0输出的偏移量(或失衡),而U1则是偏移量的温度系数(OTC)。
式1使用一次多项式来对传感器进行建模。有些应用场合可能会用到高次多项式、分段线性技术、或者分段二次逼近模型,并为其中的系数建立一个查寻表。无论使用哪种模型,数字校准时都要对VOUT、VB和T进行数字化,同时要采用某种方式来确定全部系数,并进行必要的计算。式2由式1整理并解出P。从式2可以更清楚地看到,为了得到精确的压力值,数字计算(通常由微控制器(μC)执行)所需的信息。
P = (VOUT/VB-U0-U1×(T-T0))/(S0×(1+S1×(T-T0)) (式2)
电压驱动
图1电路中的电压驱动方式使用一个高精度ADC来对VOUT(AIN1/AIN2)、温度(AIN3/AIN4)和VB (AIN5/AIN6)进行数字化。这些测量值随后被传送到μC,在那里计算实际的压力。电桥直接由电源驱动,这个电源同时也为ADC、电压基准和μC供电。电路图中标有Rt的电阻式温度检测器用来测量温度。通过ADC内的输入复用器同时测量电桥、RTD和电源电压。为确定校准系数,整个系统(或至少是RTD和电桥)被放到温箱里,向电桥施加校准过的压力,并在多个不同温度下进行测量。测量数据通过测试系统进行处理,以确定校准系数。最终的系数被下载到μC并存储到非易失性存储器中。
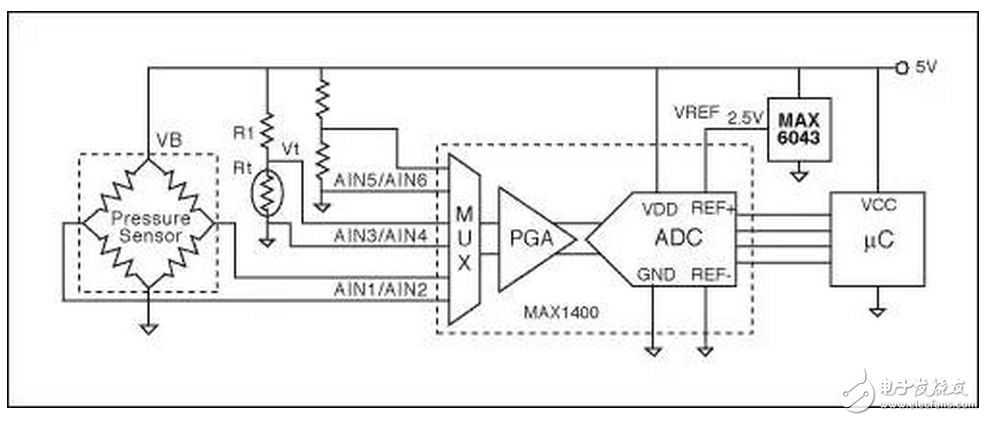
图1. 该电路直接测量计算实际压力所需的变量(激励电压、温度和电桥输出)
设计该电路时主要应考虑的是动态范围和ADC的分辨率。最低要求取决于具体应用和所选的传感器和RTD的参数。为了举例说明,使用下列参数:
系统规格
满量程压力:100psi
压力分辨率:0.05psi
温度范围:-40°C到+85°C
电源电压:4.75到5.25V
压力传感器规格
S0 (灵敏度): 150到300μV/V/psi
S1 (灵敏度的温度系数): 最大-2500ppm/°C
U0 (偏移): -3到+3mV/V
U1 (偏移的温度系数): -15到+15μV/V/°C
RB (输入电阻): 4.5k
TCR (电阻温度系数): 1200ppm/°C
RTD: PT100
α: 3850ppm/°C (ΔR/°C = 0.385,Ω额定值)
-40°C时的值: 84.27Ω
0°C时值: 100Ω
85°C时值: 132.80Ω
电压分辨率
能够接受的最小电压分辨率可根据能够检测到的最小压力变化所对应的VOUT得到。极端情况为使用最低灵敏度的传感器,在最高温度和最低供电电压下进行测量。注意,式1中的偏移项不影响分辨率,因为分辨率仅与压力响应有关。
使用式1以及上述假设:
ΔVOUTmin=4.75V(0.05psi/count150μV/V/psi ×(1+(-2500ppm/°C)×(85°C-25°C))≈30.3μV/count
所以: 最低ADC分辨率=30μV/count
输入范围
输入范围取决于最大输入电压和最小或者最负的输入电压。根据式1,产生最大VOUT的条件是:最大压力(100psi)、最低温度(-40°C)、最大电源电压(5.25V)和3mV/V的偏移、-15μV/V/°C的偏移温度系数、-2500ppm/°C的TCS、以及最高灵敏度的芯片(300μV/V/psi)。最负信号一般都在无压力(P=0)、电源电压为5.25V、-3mV/V的偏移、-40°C的温度以及OTC等于+15μV/V/°C的情况下出现。
再次使用公式1以及上述假设:
VOUTmax=5.25V×(100psi·300μV/V/psi×(1+(-2500ppm/°C)×(-40°C-25°C))+3mV/V+(-0.015mV/V/°C)×(-40°C-25°C))-204mV
VOUTmin =5.25×(-3mV/V+(0.015mV/V/°C×(-40°C-25°C)))--21mV
因此:ADC的输入范围=-21mV到+204mV
分辨位数
适用于本应用的ADC应具有-21mV到+204mV 的输入范围和30μV/count的电压分辨率。该ADC的编码总数为(204mV + 21mV)/(30μV/count)=7500counts,或稍低于13位的动态范围。如果传感器的输出范围与ADC的输入范围完全匹配,那么一个13位的转换器就可以满足需要。由于-21mV到+204mV的量程与通常的ADC输入范围都不匹配,因此需要或者对输入信号进行电平移动和放大,或者选用更高分辨率的ADC。幸运的是,现代的Σ-Δ转换器的分辨率高,具有双极性输入和内部放大器,使高分辨率ADC的使用变为现实。这些Σ-Δ ADC提供了一个更为经济的方案,而不需要增加其它元器件。这不仅减小了电路板尺寸,还避免了放大和电平移位电路所引入的漂移误差。
工作于5V电源的典型Σ-Δ转换器,采用2.5V参考电压,具有±2.5V的输入电压范围。为了满足我们对于压力传感器分辨率的要求,这种ADC的动态范围应当是:(2.5V-(-2.5V))/(30μV/count)=166,667counts。这相当于17.35位,很多ADC都能满足该要求,例如18位的MAX1400。如果选用SAR ADC,则是相当昂贵的,因为这是将18位转换器用于13位应用,且只产生11位的结果。然而,选用18位(17位加上符号位)的Σ-Δ转换器更为现实,尽管三个最高位其实并没有使用。除了廉价外,Σ-Δ转换器还具有高输入阻抗和很好的噪声抑制特性。
18位ADC可以使用带内部放大器的更低分辨率的转换器来代替,例如16位的MAX1416。8倍的增益相当于将ADC转换结果向高位移了3位。从而利用了全部的转换位并将转换需求减少到15位。是选用无增益的高分辨率转换器,还是有增益的低分辨率转换器,这要看在具体使用的增益和转换速率下的噪声规格。Σ-Δ转换器的有效分辨率通常受到噪声的限制。
温度测量
如果测量温度仅仅是为了对压力传感器进行补偿,那么,温度测量不要求十分准确,只要测量结果与温度的对应关系具有足够的可重复性即可。这样将会有更大的灵活性和较松的设计要求。有三个基本的设计要求:避免自加热、具有足够的温度分辨率、保证在ADC的测量范围之内。
使最大Vt电压接近于最大压力信号有利于采用相同的ADC和内部增益来测量温度和压力。本例中的最大输入电压为+204mV。考虑到电阻的误差,最高温度信号电压可保守地选择为+180mV。将Rt上的电压限制到+180mV也有利于避免Rt的自加热问题。一旦最大电压选定,根据在85°C (Rt=132.8Ω),VB=5.25V的条件下产生该最大电压可以计算得到R1。R1的值可通过式3进行计算,式中的Vtmax是RT上所允许的最大压降。温度分辨率等于ADC的电压分辨率除以Vt的温度敏感度。式4给出了温度分辨率的计算方法。(注意:本例采用的是计算出的最小电压分辨率,是一种较为保守的设计。你也可以使用实际的ADC无噪声分辨)
R1=Rt×(VB/Vtmax-1) (式3)
R1=132.8Ω×(5.25V/0.18V-1)≈3.7kΩ
TRES=VRES×(R1+Rt)2/(VB×R1×ΔRt/°C) (式4)
这里,TRES是ADC所能分辨的摄氏温度测量分辨率。
TRES=30μV/count×(3700Ω+132.8Ω)2/(4.75VΩ 3700Ω×0.38Ω/°C)≈0.07°C/count
0.07°C的温度分辨率足以满足大多数应用的要求。但是,如果需要更高的分辨率,有以下几个选择:使用一个更高分辨率的ADC;将RTD换成热敏电阻;或将RTD用于电桥,以便在ADC中能够使用更高的增益。
注意,要得到有用的温度结果,软件必须对供电电压的变化进行补偿。另外一种代替方法是将R1连接到VREF,而不是VB。这样可使Vt不依赖于VB,但也增加了参考电压的负载。
优化的电压驱动
硅应变计和ADC的一些特性允许图1电路进一步简化。从式1可以看出,电桥输出与供电电压(VB)直接成正比。具有这种特性的传感器称为比例传感器。式5为适用于所有具有温度相关误差的比例传感器的通用表达式。在式1中,将VB右边的所有部分用通用表达式f(p,t)代替便是式5。这里,p是被测物理量的强度,而t则为温度。
VOUT=VB×?(p,t) (式5)
ADC也具有比例属性,它的输出与输入电压和参考电压的比直接成比例。式6描述了一般的ADC的数据读取值(D)与输入信号(Vs)、参考电压(VREF)、满量程读数(FS)、以及比例因子(K)之间的关系。该比例因子与具体的转换器架构以及内部放大倍数有关。
D=(Vs/VREF)FS×K (式6)
将式6中的Vs用式5中的VOUT表达式代换,ADC对于性能的影响就会显现出来。结果见式7:
D=(VB/VREF)×?(p,t)×FS×K (式7)
由式7可见,对于测量结果而言,更为重要的是VB和VREF的比值,而非它们的绝对值。因此,图1电路中的电压基准源可以不用。ADC的参考电压可以取自一个简单的电阻分压器,只要保持恒定的VB/VREF之比即可。这一改进不仅省去了电压基准,也免去了对VB的测量,以及补偿VB变化所需的所有软件。这种技术适用于所有比例传感器。RT和R1串联构成的温度传感器也是比例型的,因此,温度检测也不需要电压基准。该电路如图2所示。

图2. 比例测量电路示例。
压力传感器的输出、RTD电压、以及ADC参考电压均与供电电压直接成正比该电路无需绝对电压基准,同时简化了确定实际压力时所必需的计算。
省去RTD
硅基电阻对温度十分敏感,根据这种特性,可用电桥电阻作为系统的温度传感器。这不仅降低了成本,而且会有更好的效果。因为它不再受RTD和压敏电桥之间温度梯度的影响。正像前面所提到的,温度测量的绝对精度并不重要,只要温度测量是可重复的和唯一的。这种唯一性要求限定了这种温度检测方法只能用于施压后桥路电阻保持恒定的电桥。幸运的是,大多数硅传感器采用全工作桥,能够满足该要求。
图3电路中,在电桥低压侧串联一个电阻(R1),从而得到一个温度相关电压。增加这个电阻会减小电桥电压,从而减小其输出。减小的幅度一般不是很大,况且只需略微增加增益或减小参考电压就足以对其加以补偿。式8可用于计算R1的保守值。对于大多数应用,当R1小于RB/2时,电路能很好地工作。
R1=(RB×VRES)/(VDD×TCR×TRES-2.5×VRES) (式8)
这里,RB是传感器电桥的输入电阻,VRES是ADC的电压分辨率,VDD是供电电压,TCR为传感器电桥的电阻温度系数,而TRES是所期望的温度分辨率。
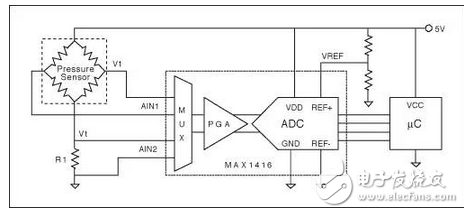
图3. 用电桥输出测量压力和用电桥电阻测量温度的比例电路实例
继续上述实例并假定希望得到0.05°C的温度分辨率,R1=(4.5kΩ×30μV/count)/(((5V×1200ppm/°C×0.05°C/count)-2.5)×30μV/count)=0.6kΩ。由于R1小于RB的一半,这一结果是有效的。在该例中,R1的增加使VB下降12%。在选择转换器时,可以将17.35位的分辨率要求向上舍入为18位。增加的分辨率用于补偿VB降低的影响绰绰有余。
温度上升时,电桥电阻的上升使电桥上的电压降也上升。这种VB随温度的变化形成了一个附加的TCS项。正好该值为正值,而传感器的固有TCS值是负数,这样,将一个电阻与传感器串联实际会减小未经补偿的TCS误差。上面的校准技术仍然有效。只是需要补偿的误差略小了一些。
电流驱动
有一类特殊的压阻式传感器被称为恒流传感器或电流驱动传感器。这些传感器经过特殊处理,当它们采用电流源驱动时,灵敏度在温度变化时保持恒定(TCS ≈ 0)。电流驱动传感器经常增加附加电阻,可以消除或者显著降低偏移误差和OTC误差。这实际上是一种模拟的传感器校准技术。这可以将设计者从繁杂的工作中解放出来,不必对每个传感器在不同温度和压力下进行测量。这种传感器在宽温范围内的绝对精度通常不如数字校准的传感器好。数字技术仍然能用于改善这些传感器的性能,通过测量电桥上的电压很容易获得温度信息,其灵敏度通常大于2000ppm/°C。图4所示是一种电流驱动的电桥电路。该电路使用同一个电压基准源来建立恒定电流和为ADC提供基准电压。
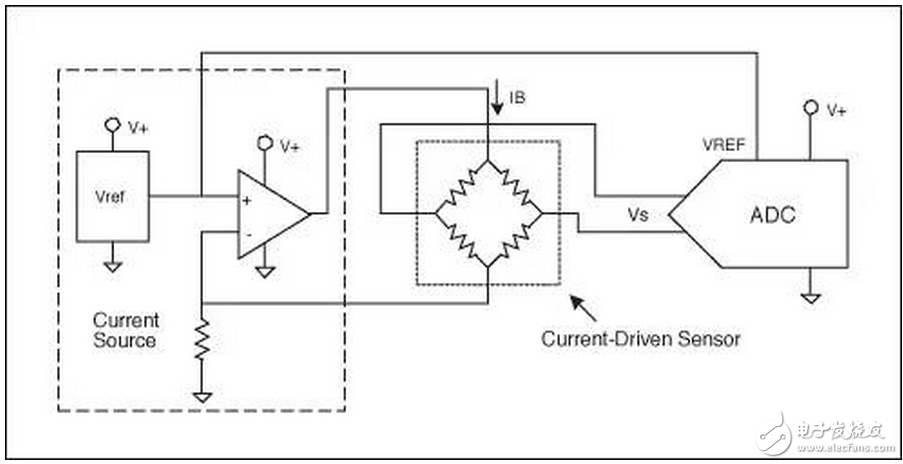
图4. 该电路使用了一个电流驱动传感器,采用传统的电流源电路驱动
省去电流源
理解了电流驱动式传感器如何对STC进行补偿,就可以采用图5电路在不带电流源的情况下达到与图4电路相同的效果。电流驱动传感器仍具有一个激励电压(VB),只是VB并不固定于电源电压。VB由电桥阻抗和流过电桥的电流来决定。如前所述,硅电阻具有正温度系数。这样,当电桥由电流源供电时,VB将随温度的升高而增加。如果电桥的TCR (阻抗温度系数)与TCS幅值相等而符号相反,那么,VB将随着温度以适当的比率增加,对灵敏度的降低进行补偿。在某个有限的温度范围内,TCS将接近零。

图5. 此电路采用电流驱动传感器,但无需电流源和电压参考
从7出发,将其中的VB用IB×RB来代换,即可得到图4电路中的ADC输出方程。可得到公式9,其中,RB是电桥的输入电阻,IB是流经电桥的电流。
D=(IB×RB/VREF)×?(p,t)×FS×K (式9)
图5电路能够提供与图4电路相同的性能,而不需要电流源或电压参考。这可以通过比较两个电路的输出来说明。图5中的ADC输出可由式7出发得到,将其中的VB和VREF替代为相应的表达式即可。结果如式10:
重复式7: D=(VB/VREF)×f(p,t)×FS×K
对于图5电路: VB=VDD×RB/(R1+RB)
和VREF=VDD×R1/(R1+RB)
将它们代入等式7可得到式10:
D=(RB/R1)×?(p,t)×FS×K (式10)
如果选择R1等于VREF/IB,那么式9和式10是完全相同的,这就表明,图5电路也会得出和图4电路相同的结果。为了得到相同的结果,R1必须等于VREF/IB,但这不是温度补偿所要求的。只要RB乘以一个温度无关的常数,就可以实现温度补偿。R1可选择最适合于系统要求的电阻值。
当使用图5电路时,要记住ADC的参考电压随温度变化。这使得ADC不适合用来监测其它系统电压。事实上,如果需要进行温度敏感测量来实现额外的补偿,可以使用一个额外的ADC通道来测量供电电压。还有,在使用图5电路时,必须注意要确保VREF位于ADC的规定范围之内。
结论
硅压阻式应变计比较高的输出幅度使其可以直接和低成本、高分辨率Σ-ΔADC接口。这样避免了放大和电平移位电路带来的成本和误差。另外,这种应变计的热特性和ADC的比例特性可被用来显著降低高精度电路的复杂程度。
