五、平衡电桥的等效电阻
1.电桥的概念
电桥电路的构成特点是:4个节点,5条支路。图8所示电路就是一个电桥电路,其中,a-c、c-b、b-d和d-a节点间所接支路为桥臂电阻,c-d间所接支路为桥电阻。
对于一般电桥电路,只能按上述方法求等效电阻。而当电桥平衡时,计算则大为简化。
2.电桥平衡及平衡条件
在电桥电路中,如图10所示,如果桥支路两端的电位值相等,即Vc=Vd,则电桥就处于平衡状态。
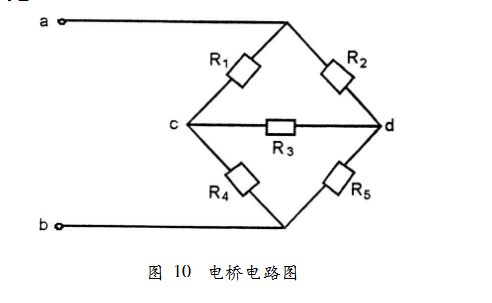
那么,在什么情况下电桥可以达到平衡?根据电桥平衡概念,很容易推得电桥平衡条件是当相邻电阻成比例,或对臂电阻乘积相等时,电桥达到平衡状态。
由此可知,图8所示电桥不满足平衡条件。但是,如果将R4和R5分别改为258和208(如图11所示),此时,R1@R5=R2@R4,或者R1/R4=R2/R5,该电桥达到平衡条件,就是平衡电桥。
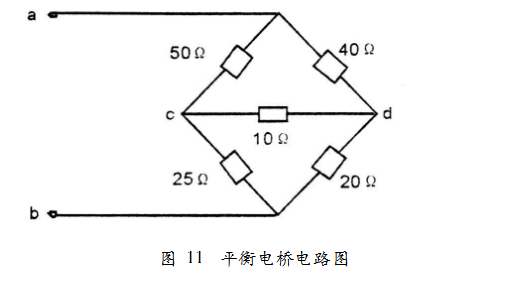
3.平衡电桥电阻计算
电桥平衡时,可以不必用上述电阻星形三角形变换方法计算等效电阻,而是利用电桥平衡特点来计算,具体可以采用以下两种方法:
(1)由于c、d等电位(即Ucd=0),因此可用一根导线将两点直接短接,如图12所示
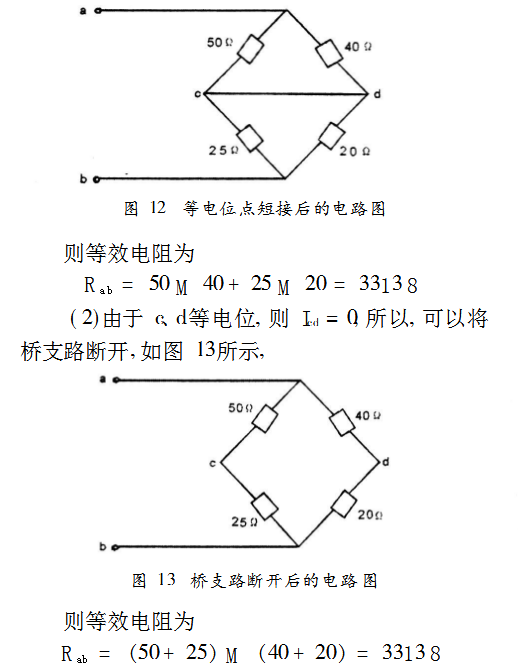
说明:
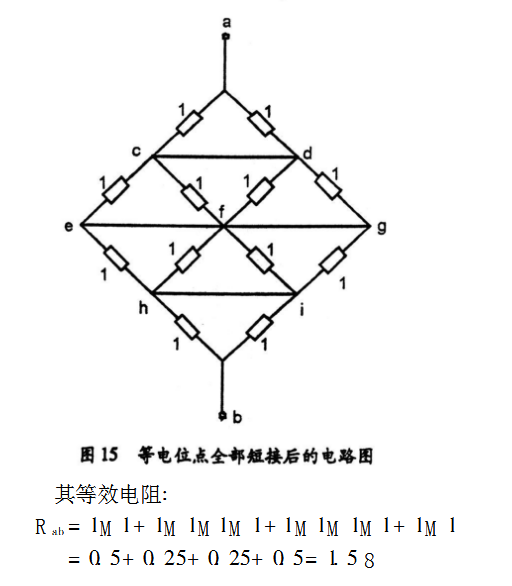
如果电路中含有几个平衡电桥,同样可以根据平衡特点,将各等电位点短接或者断开。例如,图14所示电路,其中就含有四个平衡电桥,计算时可将等电位点全部短接,如图15所示。
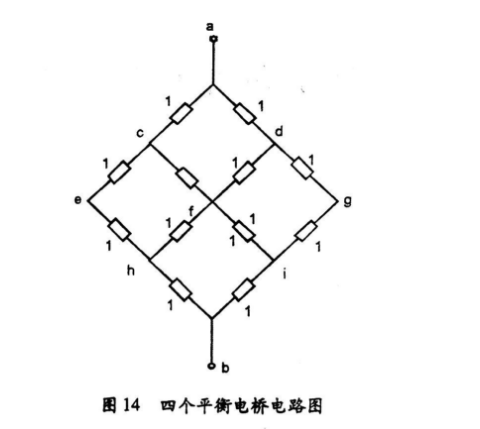
具有对称结构的电路
观察可知,图14所示就是一个具有左右对称、上下也对称的电路。计算这种电路时,还可以利用电路对称特点,使计算变得更简便。
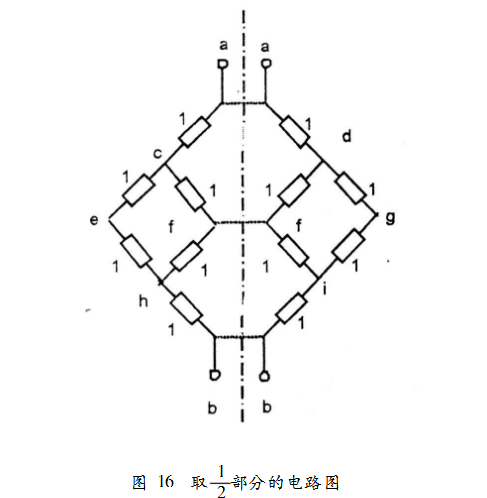
(1)如果只考虑左右对称,则用一假想平面将电路沿对称轴分成左右两部分,如图16所示,然后求出其中一半的等效电阻,即:
Rcabc=1+(1+1)M(1+1)+1=38最后,求得总等效电阻为:
Rab=Rcabc/2=1.58(2)
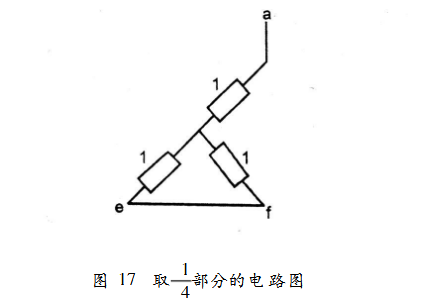
如果同时还考虑该电路上下也对称的特点,那么计算就更简单了,计算时只需取四分之一部分即可,如图17所示。
Rab=Rae=1+1M1=1.58
综上所述,在实际等效电阻计算中,只有根据电路的具体形式及电阻之间的联接关系,选择正确、恰当的计算方法,掌握灵活、简便的运算技巧,才能准确而又快速地进行分析和计算。当然熟练掌握和运用这些方法和技巧不是一蹴而就的,需要花一定的时间,下一番功夫,加强训练,不断总结,才能逐步积累经验,真正掌握等效电阻的计算方法和技巧。
