这个问题起源于上一个冰河时代中期的某个时候,就在成功的乳齿象狩猎之后。循环分析或节点分析将产生与此处所示相同的答案,但需要更多的脑力劳动。有时,如果我们保持警惕,会有更简单的方法。
这个问题实际上证明了对称性在某些电路分析中可以提供的好处。也就是说,由 12 个相等的电阻组成的立方体对角之间的电阻是多少(图 1)
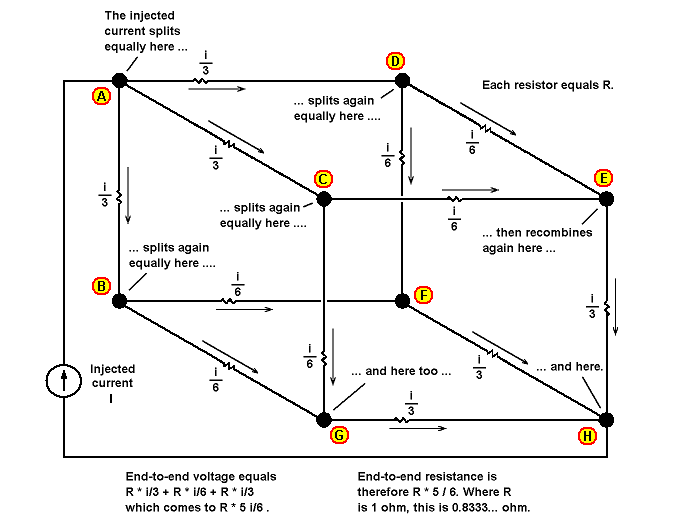
图 1一个电阻立方体,每个边缘由 12 个相等的电阻组成,提示我们确定每个角的电阻。资料约翰·邓恩
您可以编写节点或循环方程来解决这个问题,但过程会很繁琐。您必须原谅我,但使用 SPICE 是作弊行为,至少在我看来是这样。试图看看哪些内容与哪些内容同时发生可能会让你语无伦次。然而,使用一些简单的观察并识别对称性适用的位置将顺利地得出正确的结果。
在图 1 中,我们选择节点 A 和节点 H 作为立方体的对角。我们向这些相对的角落注入电流,为了让事情变得简单,我们让电流为一安培。
首先,我们看看当前的部门。
因为我们具有对称性,所以我们可以说,远离节点 A 的三个电阻将分别承载注入电流的三分之一。节点 B、节点 C 和节点 D 将从各自连接回节点 A 的电阻接收三分之一安培的电流。
同样,由于对称性,我们可以进一步指出,远离节点 B、节点 C 和节点 D 的两个电阻将分别承载其各自节点到达电流的一半。节点 B 将分别向节点 F 和节点 G 传送六分之一安培,节点 C 将分别向节点 E 和节点 G 传送六分之一安培,节点 D 将分别向节点 E 传送六分之一安培和节点F。
接下来,我们看看当前的总结。
节点 E 将接收来自节点 C 和节点 D 的两个六分之一安培的电流,节点 F 将接收来自节点 B 和节点 D 的两个六分之一安培的电流,而节点 G 将接收来自节点 B 和节点 D 的两个六分之一安培的电流。 - 节点 B 和节点 C 各六分之一安培。
节点 H 将从节点 E、节点 F 和节点 G 接收三个各三分之一安培的电流。
可以肯定的是,这整个推理链在语言上是拗口的,但对图 1 进行目视检查将使这一切变得非常容易理解。
如果我们让每个电阻器为一欧姆,则承载三分之一安培的每个电阻器上的压降将为三分之一伏,而承载六分之一安培的每个电阻器上的压降将为三分之一伏特。六伏特。
如果我们将从节点 H 到节点 A 的电压降相加,无论我们选择什么路径,结果都是六分之五伏。因此,立方体的角对角电阻达到一欧姆的六分之五。
