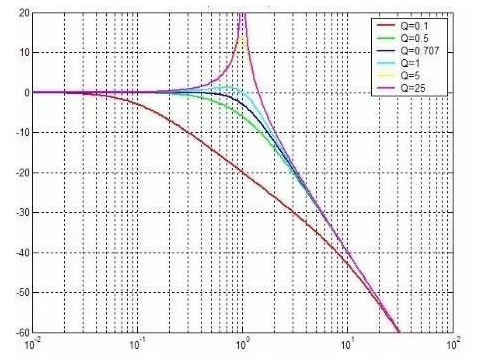
零点和极点对频率响应的影响可以总结为：
*当频率远小于某零点/极点的模时，该零点/极点对频率响应的影响可以忽略。
*当频率接近某极点的模时，该极点的效果渐渐体现。当频率远大于该极点时，该极点使得频率响应的幅度以20dB/dec的速度衰减，而相位相对DC产生-π/2的变化。
*共轭极点是一种特殊的极点，它们总是成对出现且共轭极点对的模都相等，因此当频率远大于一对共轭极点的模的时候，该共轭极点对会使频率响应的幅度以40dB/dec的速度衰减，而相位相对DC产生-π的变化。而在频率接近共轭极点对的模的时候，频率响应曲线的变化取决于共轭极点对的位置（详见下文）。
*当频率接近某零点的模时，该零点的效果渐渐体现。当频率远大于该零点时，该零点使得频率响应的幅度以20dB/dec的速度增加。而相位相对DC产生π/2（当零点在左半平面）或-π/2（当零点在右半平面）的变化。
*频率响应的总体幅度/相位取决于所有零点和极点对幅度/相位的贡献。
共轭极点对
共轭极点对是一类特殊的极点。一对共轭极点（s-p）（s-p*）可以写作
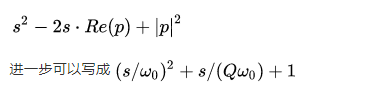其中ω0为共轭极点的谐振频率，Q称作共轭极点的品质因数。
共轭极点对模型最初来源于LC谐振电路，如下图中的RLC串联电路。
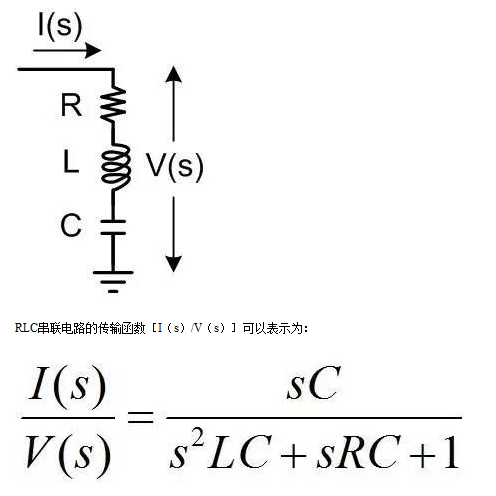
其中共轭极点的谐振频率ω0=1/√LC即LC tank的谐振频率，品质因数Q=（1/R）∙√（L/C）即为LC tank的品质因数，表示在谐振频率附近每周期LC tank存储的能量与耗散能量的比值。共轭极点可以由LC tank形成，也可由反馈通路形成。
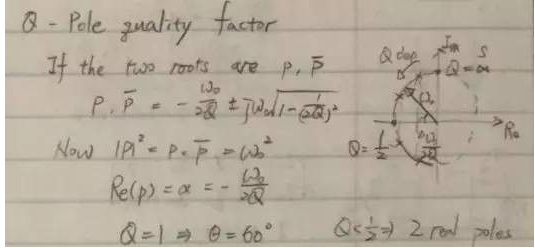
共轭极点对的Q值由共轭极点的位置决定。当共轭极点的谐振频率固定而改变品质因数（即固定L和C而改变R）时，共轭极点对的轨迹在以原点为圆心，半径为ω0的圆上。当共轭极点对靠近纵轴时，品质因数变大；而当共轭极点对靠近横轴时，品质因数变小。共轭极点对的品质因数必须大于等于1/2，当Q小于1/2时共轭极点对退化为两个实极点。
对于传输函数具有共轭极点对的系统，系统的自然响应中含有包络指数衰减的正弦波。有时候在放大器的瞬时响应中会看到衰减震荡的现象，这种现象就是由共轭极点造成的。
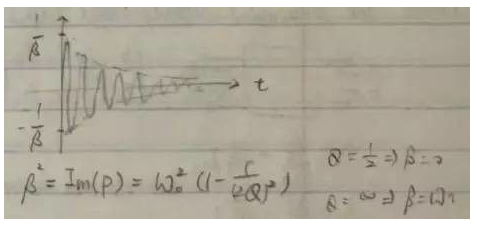
正弦波的频率接近谐振频率ω0，而包络的衰减速度取决于Q。Q值约等于包络衰减到初始值的1/e时所需要的谐振周期。Q值大时包络衰减较慢，反之Q值小时包络衰减较快。在放大器设计中我们往往希望看到settling time比较小的瞬时响应，因此应该避免高Q值得共轭极点对。
共轭极点对另一个重要性质是它会引起频率响应的尖峰（peaking）。这一点可以从零极点图来理解。
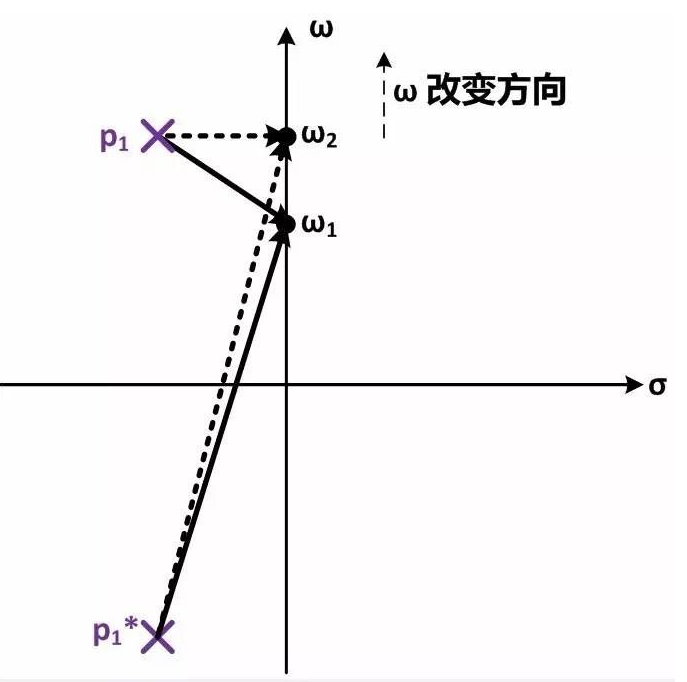
在零极点图上，有共轭极点p1和p1*，位置在σ±jω0。当频率从ω1（略小于ω0）移动到ω2（等于ω0）时，连接到极点p1*的极点向量长度基本不变，但连接到极点p1的极点长度显著变短了。因此频率响应在谐振频率（ω=ω0）处会产生一个尖峰，尖峰的高度随Q值变大而变大。极端情况是Q值无穷大时，此时p1和p1*都在ω轴上，因此当ω=ω0时，连接p1和ω的极点向量长度为0，这样频率响应的幅度变为无穷大，所以就产生了高度无穷大的尖峰。在设计需要较小settling time的放大器时我们希望避免明显的频率响应尖峰（频率响应尖峰明显=》共轭极点对Q值大=》瞬时响应中衰减震荡持续时间较长=》settling time较长）；但另一方面在设计宽带放大器（例如在CML电路中）时我们往往会故意引入频率响应尖峰以增加带宽。
