由传感器所检测到的奇异信号往往载有设备运行状态特征的重要信息。判断状态信号的奇异点出现时刻,并对信号奇异性实现定量描述,在信号处理和故障诊断等领域有着重要的意义。
信号的奇异性分析是提取信号特征的重要手段,傅里叶变换一直是研究信号奇异性的经典工具,但是由于傅里叶变换对信号的表示要么在时域,要么在频域,缺乏空间局部特性,因而只能确定信号奇异性的整体信息,无法确定奇异点的空间分布。小波变换具有时-频局部化特性,能够有效地分析信号的奇异性,确定奇异点的位置与奇异度的大小,为信号奇异性分析提供了有力的工具。
一 基本理论
(1) 小波分析概况
小波分析是自1986年以来由Meyer,Mallat及Daubechies等的研究工作为基础而迅速发展起来的一门新兴学科,他是傅里叶分析(Fourier Analysis) 划时代的发展结果,是目前数学分析和信号处理领域中广泛应用的一套新理论、新方法,如:信号分析、图像处理、量子力学、军事电子对抗与武器的智能化、计算机分类与识别、数据压缩、医学成像与诊断、地震勘探数据处理、边缘检测、音乐与语音人工合成、大型机械的故障诊断、大气与海洋波的分析、分形力学、流体湍流以及天体力学等。但以上大多数领域的应用都可以归结为信号处理问题,故本文才重点介绍小波分析在信号处理方面的应用。
在信号处理领域,对原始信号进行变换,从变换的结果和过程中提取信号的特征,获得更多的信息,而这些信息是原来信号没有直接提供的(隐含的),目前,已经有许多变换应用于信号处理,最基本的是频域变换和时域变换,最熟悉的莫过于傅里叶变换(Fourier Transform),然而,傅里叶变换只能分别对信号的时域和频域进行观察,不能把二者有机地结合起来。为了解决此问题,引入了短时傅里叶变换(Short-time Fourier Transform),该变换能够给出信号的时间和频率的二维分布,在短时傅里叶变换中,其窗口宽度是一个恒定的值,不能根据信号局部特征调整其窗口宽度。为此,引入了小波变换,解决了以上问题。
小波分析方法是一种窗口大小(即窗口面积)固定但其形状可改变、时间窗和频率窗都可改变的时频局部分析方法。即在低频部分具有较高的频率分辨率和较
低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,所以被誉为数学显微镜。在大尺度下,可以将信号的低频信息(全局)表现出来,在小尺度下,可以将信号的高频(局部)特征反映出来。 (2) 信号奇异性的有关定义
数学上称无限次可导函数是光滑的或没有奇异性,若函数在某处有间断或某阶导数不连续,则称函数在此处有奇异性,该点就是奇异点。信号的突变点往往包含重要的信息。宇宙射线和太阳黑子爆发,空间核磁暴,对于在太空飞行的卫星和飞船安全构成重大威胁,影响太空飞行器的使用寿命。通过处理采集的空间数据,检测到奇变点,找到太空天气异动的时刻,做出科学的判断,及时调整飞行器姿态,以保护飞行器的安全。寻找变化周期,总结规律,可为进行太空天气预报提供依据。
假设一维信号s(t)=s0(t)+n(t),n(t)为噪声。s0(t)在t的某一邻域内二阶可导,
一阶导数‘
0()St的极值代表了在极值某一相邻区间内,信号线性变化最剧烈的时刻。我们往往对信号变化最剧烈的时刻,也就是’0()St的模‘0()St最大值所在时刻感兴趣。’0()St极值点对应于s0(t)的拐点。s0(t)的拐点对应于二阶导数‘’0()St的零点位置。‘’0()St的零点不一定是‘0()St的极值点。通过’‘0()St的零点位置以及零点邻域内值的正负性质,可以判断出s0(t)变化的凹凸特性,也可以判断该点是否是’0()St在某一邻域内的极值(极大值或极小值)。但是‘0()St的极小值并不一定成为’0()
St的最大值。
二 小波分析基础


从以上分析,用观测信号的平滑版本stt取代原信号s0(t)、1Wst和2Wst取代s0(t)的一阶和二阶导数进行分析。表1比较了含有噪声的信号和不含噪声突变点和拐点的区别。为了使结果更准确,综合考虑1Wst和2Wst多尺度计算的结果,来判断信号的突变点

三 仿真实验与结果分析
当小波函数可看作某一平滑函数的一阶导数时,信号小波变换模的局部极值
点,对应于信号的突变点;当小波函数可看作某一平滑函数的二阶导数时,信号小波变换的过零点应于信号的突变点。因此,采用小波变换模的过零点和局部极值点的方法可以检测信号的突变点。比较来说,用局部极值点的方法进行检测更具优越性。
一般信号奇异性分为两种情况:①信号在某一时刻其幅值发生突变,引起信号的不连续,这种类型的突变称为第一种类型的间断点;②信号外观上很光滑,幅值没有发生突变,但是信号的一阶微分有突变发生且一阶不连续,这种类型的突变称为第二种类型的间断点。
应用小波分析可以检测出信号中突变点的位置、类型以及变化的幅度。下面的例子将介绍用小波分析检测第一类间断点,信号幅值变化的准确时间,即间断点的准确位置。在这个例子中信号的不连续是由于低频特征的正弦信号在后半部分突然加入高频特征的正弦信号的缘故,分析的目的是将加入高频特征的正弦信号的时间检测出来。在MATLAB的命令窗口拟进行如下编程:
load freqbrk; %装载文件名为freqbrk的信号


该程序是用db(Daubechies)小波对信号第一类间断点进行分析,结果如下:
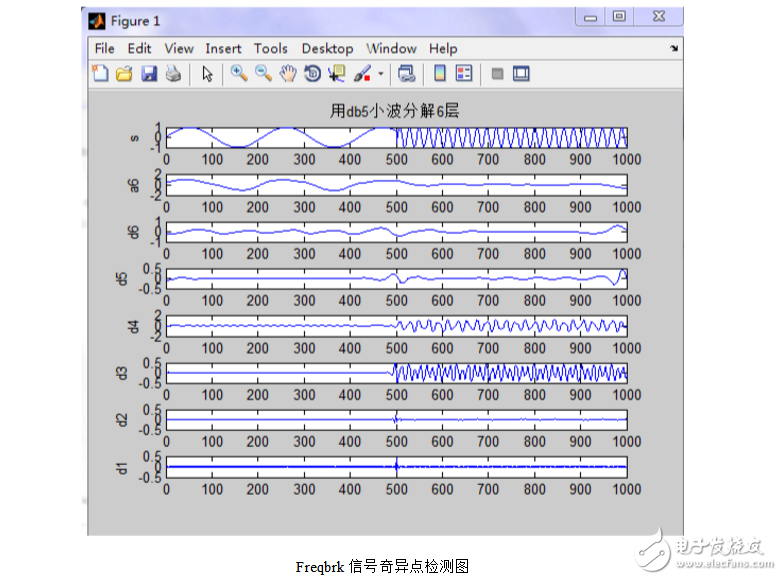
从结果波形图上可以看出,信号的不连续点在500t。使用db6小波将信
号进行6层分解,来检测第一种类型的间断点,可以非常清楚地观察到信号的不连续点,即高频特征的正弦信号的加入点,这是因为间断点包含了高频信息。如果只需要识别第一种类型的间断点,则可以非常清楚地观察到信号的不连续点,即高频特征的正弦信号的加入点,这是因为间断点包含了高频信息。如果只需要识别信号的不连续点,用db1小波比用db6小波效果好。
原始信号是由两个独立的满足指数方程的信号在t=500处连接起来的,因此它看上去是光滑的,但它的一阶微分有突变。采用db6小波对信号分解后,在信号的第一层高频系数d1中可以明显的看到t=500的间断点。要注意的是,在信号奇异点的检测中,选择小波的正则性非常重要,因为这时小波可实现一个长的冲
激响应滤波器。
四 结束语
从实际数据的图形结果,可看出:2Wst的结果能够精确定位拐点,但是拐点不一定是突变点,只有表现为凸特性的拐点才是突变点;而突变点一定是拐点。1Wst和1Wst是很难精确定位突变点的位置,但是可以判断拐点是否为突变点。所以,要综合考虑1Wst和2Wst在尺度上的计算结果,2Wst用于精确定位拐点(鉴别凸性的拐点),而1Wst和1Wst用于判断该拐点是否是模极大,是否是突变点。这样既可以保证结果稳健,又能精确定位奇异点的位置。 信号奇异点可通过信号的小波变换局部极大值来定位,而奇异性运用该点的Lipschitz α来定量描述。运用该理论来实现信号的奇异性检测,比常规手段更优越。需要注意的是:选择不同的小波分析信号的奇异性及奇异性位置和奇异度的大小,其检测效果也不一样,因此,选择合适的小波非常重要。
