热敏电阻的原理及和阻值的关系如下:
一、热敏电阻的原理热敏电阻将长期处于不动作状态;当环境温度和电流处于c区时,热敏电阻的散热功率与发热功率接近,因而可能动作也可能不动作。热敏电阻在环境温度相同时,动作时间随着电流的增加而急剧缩短;热敏电阻在环境温度相对较高时具有更短的动作时间和较小的维持电流及动作电流。
二、热敏电阻和阻值的关系:热敏电阻器的典型特点是对温度敏感,不同的温度下表现出不同的电阻值。正温度系数热敏电阻器(PTC)在温度越高时电阻值越大,负温度系数热敏电阻器(NTC)在温度越高时电阻值越低,它们同属于半导体器件。
热敏电阻的电阻-温度特性可近似地用下式表示:R=R0exp{B(1/T-1/T0)}:R:温度T(K)时的电阻值、Ro:温度T0、(K)时的电阻值、B:B值、*T(K)=t(ºC)+273.15。实际上,热敏电阻的B值并非是恒定的,其变化大小因材料构成而异,最大甚至可达5K/°C。因此在较大的温度范围内应用式1时,将与实测值之间存在一定误差。此处,若将式1中的B值用式2所示的作为温度的函数计算时,则可降低与实测值之间的误差,可认为近似相等。
由于环境温度的变化导致热敏电阻本体的温度变化,热敏电阻一般都是半导体陶瓷做成的,当自身温度变化时,其陶瓷内部的电子迁移率会随温度的变化而变化。通常热敏电阻会分为PTC(正温度系数)和NTC(负温度系数)热敏电阻。正温度系数就是电阻值随温度升高而增大的电阻器,负温度系数电阻值随温度升高面指数降低。
解决非线性问题
如果您打算在整个温度范围内均使用热敏电阻温度传感器件,那么该器件的设计工作会颇具挑战性。热敏电阻通常为一款高阻抗、电阻性器件,因此当您需要将热敏电阻的阻值转换为电压值时,该器件可以简化其中的一个接口问题。然而更具挑战性的接口问题是,如何利用线性 ADC 以数字形式捕获热敏电阻的非线性行为。
“热敏电阻”一词源于对“热度敏感的电阻”这一描述的概括。热敏电阻包括两种基本的类型,分别为正温度系数热敏电阻和负温度系数热敏电阻。负温度系数热敏电阻非常适用于高精度温度测量。要确定热敏电阻周围的温度,您可以借助Steinhart-Hart公式:T=1/(A0+A1(lnRT)+A3(lnRT3))来实现。其中,T为开氏温度;RT为热敏电阻在温度T时的阻值;而 A0、A1和A3则是由热敏电阻生产厂商提供的常数。
热敏电阻的阻值会随着温度的改变而改变,而这种改变是非线性的,Steinhart-Hart公式表明了这一点。在进行温度测量时,需要驱动一个通过热敏电阻的参考电流,以创建一个等效电压,该等效电压具有非线性的响应。您可以使用配备在微控制器上的参照表,尝试对热敏电阻的非线性响应进行补偿。即使您可以在微控制器固件上运行此类算法,但您还是需要一个高精度转换器用于在出现极端值温度时进行数据捕获。
另一种方法是,您可以在数字化之前使用“硬件线性化”技术和一个较低精度的 ADC。(Figure 1)其中一种技术是将一个电阻RSER与热敏电阻RTHERM以及参考电压或电源进行串联(见图1)。将 PGA(可编程增益放大器)设置为1V/V,但在这样的电路中,一个10位精度的ADC只能感应很有限的温度范围(大约±25°C)。
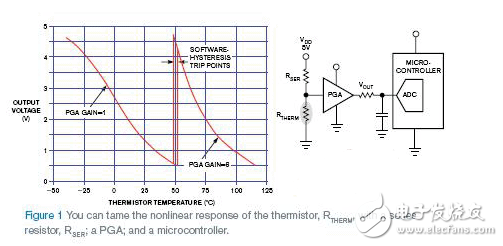
Figure 1,请注意,在图1中对高温区没能解析。但如果在这些温度值下增加 PGA 的增益,就可以将 PGA 的输出信号控制在一定范围内,在此范围内 ADC 能够提供可靠地转换,从而对热敏电阻的温度进行识别。
微控制器固件的温度传感算法可读取 10 位精度的 ADC 数字值,并将其传送到PGA 滞后软件程序。PGA 滞后程序会校验 PGA 增益设置,并将 ADC 数字值与图1显示的电压节点的值进行比较。如果 ADC 输出超过了电压节点的值,则微控制器会将 PGA 增益设置到下一个较高或较低的增益设定值上。如果有必要,微控制器会再次获取一个新的 ADC 值。然后 PGA 增益和 ADC 值会被传送到一个微控制器分段线性内插程序。
从非线性的热敏电阻上获取数据有时候会被看作是一项“不可能实现的任务”。您可以将一个串联电阻、一个微控制器、一个 10 位 ADC 以及一个 PGA 合理的配合使用,以解决非线性热敏电阻在超过±25°C温度以后所带来的测量难题。
