形位误差测量 - 滚珠螺母形位误差的CCD测量

　　本文所测为P级精度的滚珠螺母GQ25×6,文献[2]给出了其技术规范。现对其滚道圆度误差、圆柱度误差、跳动误差及同轴度误差等参数进行测量。

　　4.1　滚道圆度误差测量

　　将内螺纹装卡在分度头上,标准测球放置在滚道内,在一个螺距范围内采集N个图像,使每两次采集图像之间螺母沿固定方向旋转360°/N,计算度量测球中心点(X0,Y0)和螺母外圆柱面中心点(Xb,Yb)的亚像素坐标,以此计算形位误差。由于内螺纹外圆柱面的加工精度较高,形状误差很小,故将其视为理想圆柱面,在N个图像中,其中心的位置相对于圆周像素保持不变。以螺母外圆柱面为基准,将各图像测球中心坐标通过外圆柱面中心坐标和标定系数统一在一个坐标中,如图3所示。

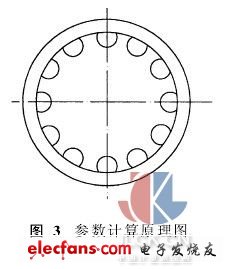
　　坐标变换的步骤是:首先对图像i (i=1,2,…,N)进行平移,使内螺纹外圆柱面中心与坐标原点重合;其次选择某个标定系数进行比例变换,使N个图像中的零件(以外圆半径为准)具有相同的像素数;然后将图像以原点为中心旋转360°(N-i) /N;最后平移回到原始位置(采集位置)。可根据各个测球中心坐标在统一坐标系中的位置求得圆度误差。

　　本文用解析方法确定各测球的分布中心(评定圆度的基准),使滚道圆度误差的评定符合最小区域法。设某一螺距范围内所有测球的球心坐标为(X0i, Y0i)(i=1,2,…,N),它们在端面上的理想分布应当在一个圆上。事实上,由于内螺纹滚道及测球的加工误差及测量误差,它们的分布是有误差的。以N个测球球心坐标(X0i, Y0i)为拟合点,利用解析方法求出测球中心分布圆的圆心(X0*, Y0*),使其在评定圆度误差时满足最小区域原则。算法步骤如下:

　　=m+1,m+2,…,N+i-1),构造直线方程L′。

　　(2)分别求L与L′垂直平分线的交点Ow,以该点为圆心经过4个点做两个圆,其半径差即为最小区域法评定的4个点的圆度误差。应时时判断每一次计算的圆度误差,满足最小区域条件时即停止计算,此时的圆心Ow即为最小区域圆圆心(X0*,Y0*),否则转步骤(3)继续计算。

　　(3)i从1到N做循环,返回步骤1重复计算。上述循环计算中,从外到内的循环次序是i-g-m-k。满足最小区域条件时,最小区域圆圆心至各测球中心距离中,至少各有两个最大值Rmax及两个最小值Rmin,且两最大值坐标点连线与两最小值坐标点连线的交点在最小圆内(最大值点与最小值点相互交替)。最小区域圆圆心(X0*, Y0*)至(X0i, Y0i)的最远点(Xmax,Ymax)距离与最近点(Xmin,Ymin)距离之差即为圆度误差,用下式表示:

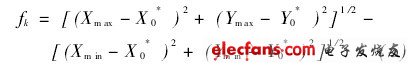
　　在内螺纹整个滚道内确定M个假想截面位置,重复测量每个位置的圆度误差,取最大值作为内螺纹公称直径的圆度误差。

　　4.2　滚道圆柱度误差测量

　　在圆度误差计算中,已经获得了M个位置的测球分布中心(X0i*, Y0i*)(i=1,2,…,M)。同计算圆度采取的方法相同,将M个位置的数据统一在一个坐标中,共得到N×M个测球中心坐标,对它们进行圆度计算,可得到内螺纹公称直径圆柱度误差。

　　4.3　滚道同轴度误差测量

　　同轴度误差是一种位置误差,它是指被测轴线对基准轴线的变动量。在圆柱度误差测量中,M个截面位置的测球分布中心(X0i*, Y0i*)是变化的,它的离散轨迹体现了被测轴线,而内螺纹外圆柱面的中心(Xb, Yb)是基准轴线。根据同轴度误差的最小区域评定法则, (X0i*, Y0i*)与(Xb, Yb)距离的最大值的两倍为内螺纹公称直径对其外径的同轴度误差。

　　4.4　滚道圆跳动误差测量

　　在圆度误差及圆柱度误差测量中,测球球心坐标(X0i, Y0i)及螺母外圆柱面中心(Xb, Yb)已经求出,根据定义,分别计算(X0i, Y0i)至(Xb, Yb)的距离Ri,则该截面滚道圆跳动误差为Rimax-Rimin。求解全部M个截面的圆跳动误差,其最大值即为内螺纹滚道对基准(内螺纹外圆柱面轴线)的径向圆跳动误差。

　　4.5　实验

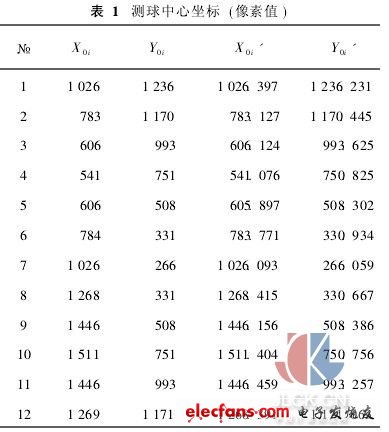
　　本实验依据提取的边缘,应用开发软件按前述几何参数的计算方法,测量了内螺纹滚道的形位误差。采集6个滚道截面进行测量(M=6),每个滚道截面采集12个图像(N=12)。图4为测球边缘坐标和中心坐标(X0i, Y0i) (i=1,2,…,N)及其亚像素值(X0i', Y0i'),内螺纹外圆柱面的亚像素中心坐标(Xb, Yb)为(1026.349,751.128)(像素值)。计算出一个螺距范围内12幅图像的测球参数,以螺母外圆柱中心为基准经过旋转、平移等变换统一到一个坐标系中,结果(像素值)如表1所示。

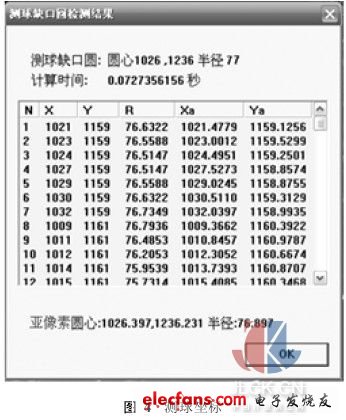
　　根据表1中数据,由整像素坐标按前述最小区域评定法求得圆度误差为: f=0.731,最小区域圆圆心坐标为(1026.134,750.866);而根据亚像素坐标求得的圆度误差为: f=0.449,最小区域圆圆心坐标为(1026.210,750.920)。该图像的标定系数k=0.025 8,按整像素计算圆度误差为0.731mm×0. 025 8= 0. 018 9mm,按亚像素计算圆度误差为0. 449mm×0. 025 8=0. 0116mm。对应表1中的数据,求各个测球中心至螺母外径中心之间的距离,其最大差值作为径向圆跳动误差值,计算结果为21. 6μm。最小区域圆圆心至螺母外径中心之间距离的2倍为该截面滚道中心相对于基准轴线的同心度误差,计算值为12. 9μm。6次亚像素测量结果见表2。

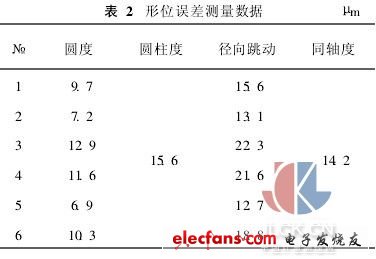
　　所测螺母形位误差结果为:圆度误差为0. 013mm,圆柱度误差为0. 016 mm,径向跳动误差为0. 022 mm,同轴度误差0. 014 mm。由文献[2]可知,本文所测螺母的几何尺寸及形位误差项目中,除圆度误差(公差为12μm)外,其余均符合技术要求。