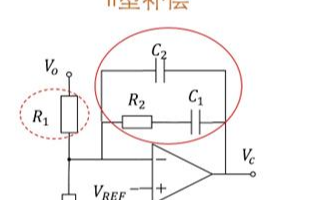
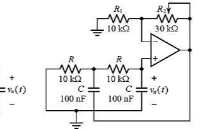
三电容电路零极点分析
现在我们来看这个纯粹的电路。假设这个电路是零状态的(relaxed),那么这个电路是线性时不变的(LTI),所以C1 C2组成了一个分压器,那么我们可以用V1来表示V2。
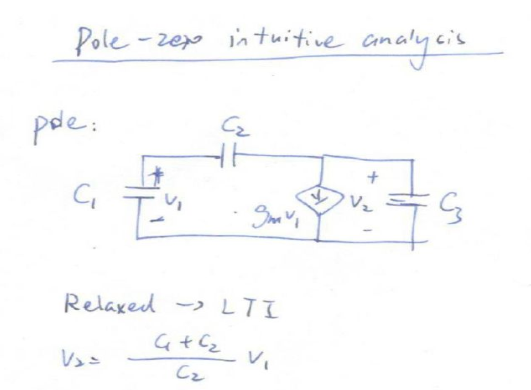
但是V2由是受控源两端的电压,而这个受控源也受到V1的控制,所以就变成了压控电流源被自己两端电压所控制。一个被自己电压控制的电流源就是一个电阻。所以我们可以算出该电阻:
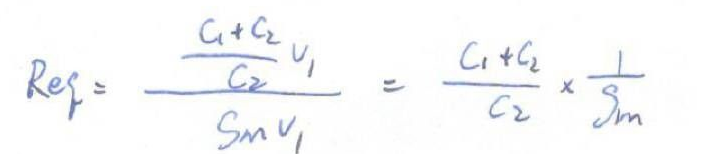
于是,三电容电路变成了下图。这个电路的时间常量很好算了,算出来果然跟我们之前算的一个极点吻合。
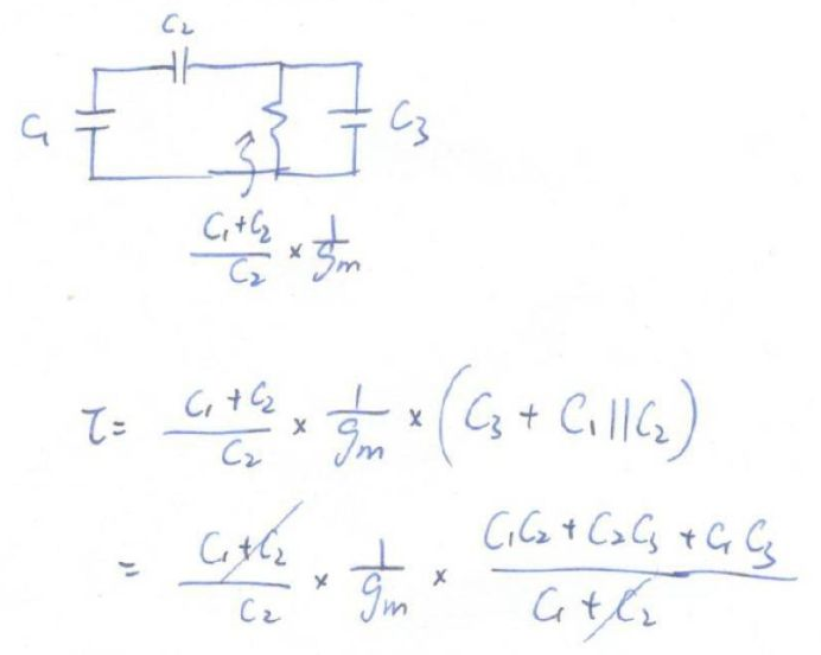
另一个极点呢?
我们现在假设C2 C3上的t=0- 时的初始状态为这样:
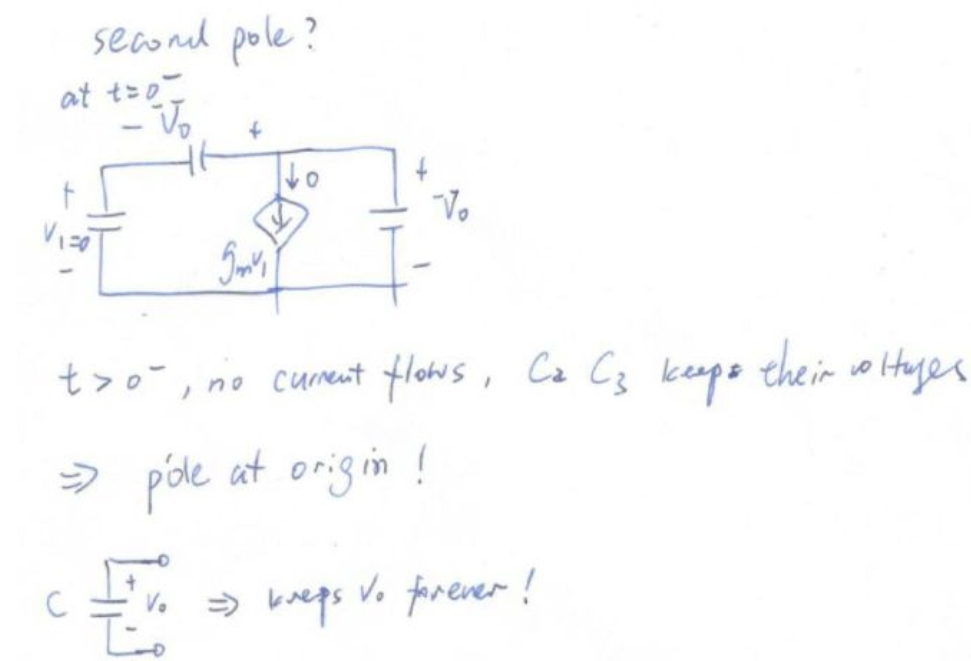
当t=0时,我们发现整个电路没有电流,C2 C3上的电压一直保持着,这种能够保持初始状态的网络,一定有一个极点在原点。我们可以举一个最简单的例子,一个电容可以保持电压,所以电容的阻抗这个网络函数有一个极点在原点。
这也与我们之前的推导吻合。
现在找零点,我们之前学过,零点是很特别的,是由激励和响应的相对位置决定的。找零点需要抵消响应。现在我们把响应V2 抵消掉,如图:
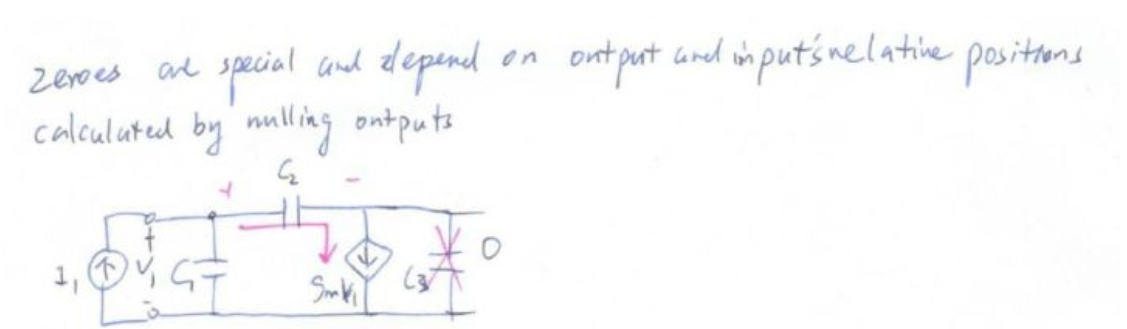
那么C3没有电流,受控源的电流等于C2的电流,但是C2的电流由可以被直接用V1表示出来,所以:
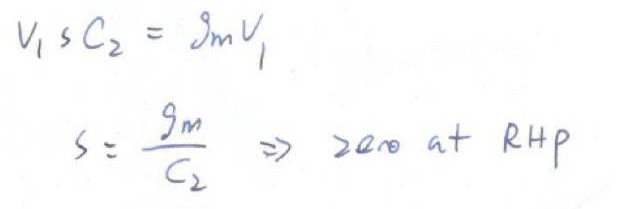
 电子发烧友App
电子发烧友App





















评论