第 3 节 戴维南定理和诺顿定理
一、戴维南定理
出发点：对于一个复杂的含有独立源的电路，如果只要计算某条支路上的电压和电流，那么就可以把电路分解成两个部分，把该条支路作为一个部分，把电路的其余部分作为另一个部分，并用一个含源二端网络 Ns 来表示。试图找到一个简化的等效电路去替换 Ns ，则该支路上的电压和电流的计算就会简单得多。
1 、戴维南定理
图 4.3-1 （ a ）中， Ns 是含源二端网络，欲计算电阻 R 的端电压 u 和端电流 i 。
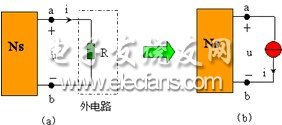
根据替代定理，可以用一个电流为 i 的理想电流源去替代外电路，如图 4.3-1 （ b ）所示，替代之后，电路中其他支路上的电压和电流则保持不变。
用叠加定理计算 a 、 b 端钮的电压 u 。
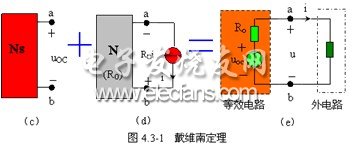
当含源二端网络 Ns 中的独立源单独作用时，外部的电流源 i 应视为开路，这时的电路如图 4.3-1 （ c ）所示。显然，这时的端钮电压就是含源二端网络 Ns 的开路电压 
。
当外部的电流源 i 单独作用时，把含源二端网络 Ns 中的所有独立源都视为 0 ，这时 Ns 中只剩下线性电阻和线性受控源等元件，没有独立源，成为一个无源二端网络，用 N 表示，其电路如图 4.3-1 （ d ）所示。显然，无源二端网络 N 可以等效为一个电阻，这个电阻称为含源二端网络 Ns 的等效内阻用 Ro 表示。这时电阻的端电压为 
。
根据叠加定理，得图 4.3-1 （ a ）电路中电阻的端电压为
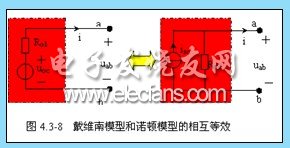
戴维南定理（Thevenin's theorem ）：对于一个线性的含源二端网络，对外电路而言，它可以用一个理想电压源和一个内阻相串联的支路来等效，这条支路称为戴维南等效支路，又称戴维南模型。其中，等效电压源的电压为该含源二端网络的开路电压 
，等效内阻为该含源二端网络中所有独立源都取 0 时的等效电阻 
。
2 、戴维南模型参数的计算
1 、电压 
的计算
先画出含源二端网络 Ns 开路时的电路，然后再计算开路电压 
。
2 、等效内阻 
的计算
（ 1 ）如果无源二端网络 N 中没有受控源，可以用电阻网络的等效方法，如电阻的串、并联方法等。
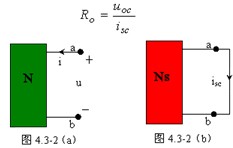
（ 2 ）外加电压法。电路如图 4.3-2 （ a ）所示，
（ 3 ）短路电流法。如图 4.3-2 （ b ）所示，
3 、应用戴维南定理时应注意的问题
1 、戴维南定理只适用于线性电路，也就是说，含源二端网络 Ns 必须是线性电路。但是，含源二端网络 Ns 以外的电路则没有限制，可以是线性电路，也可以是非线性电路。
2 、戴维南等效支路的“等效”是针对外电路而言的，即保证端钮处的电压、电流不变，而对端钮以内的电路并不等效。
3 、如果电路中含有受控源，对电路作分解时，不要把受控源和其控制量分开，否则无法求解。求含源二端网络 Ns 的等效内阻时，不能把受控源当独立源看待，即其他独立源都取 0 时，受控源应保留在电路中。
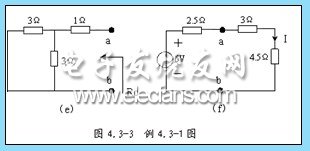
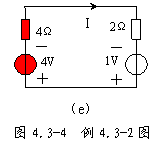
例 4.3-1 电路如图 4.3-3 （ a ）所示，试用戴维南定理求电流 I 。
 |
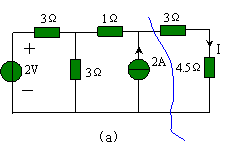解：为计算 4.5 Ω电阻上的电流 I ，可将电路分解成两个部分，如图 4.3-3 （ b ）所示。利用戴维南定理求 a 、 b 两端左侧电路的等效电路。
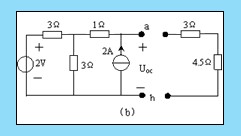
1 ．计算开路电压 
电路中 2V 电压源和 2A 电流源共同激励产生开路电压 
，由于是线性电路，可以采用叠加定理来计算。
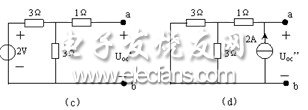
当 2V 电压源单独激励时，电流源视为开路，这时产生的开路电压为 
，如图 4.3-3 （ c ）所示。这里应注意，因为 a 、 b 端钮已开路，所以 1 Ω电阻上无电流通过，当然也就无电压。由分压公式得
又当 2A 电流源单独激励时，电压源视为短路，这时产生的开路电压为 
，如图 4.3-3 （ d ）所示。
Uoc''=2 × (1+3 ∥ 3)=5V
所以，当 2V 电压源和 2A 电流源共同激励时，由叠加定理得，开路电压为
2 ．计算等效内阻 
计算等效内阻 
时，把二端网络中的 2V 电压源和 2A 电流源都取 0 ，电路如图 4.3-3 （ e ）所示。显然，
Ro=1+3 ∥ 3=2.5 Ω
3 ．用戴维南等效支路替换图 4.3-3 （ b ）中左侧的含源二端网络，到了图 4.3-3 （ f ）所示的等效电路。所以，由全欧姆定律得电流
例 4.3-2 电路如图 4.3-4 （ a ）所示，试用戴维南定理求 1V 电压源的功率。
 |
解：欲求 1V 电压源的功率，只要求出该电压源支路的电流即可。现求 a 、 b 端钮左侧电路的戴维南等效支路。
计算 a 、 b 二端网络开路电压的电路如图 4.3-4 （ b ）所示。由 KVL 得
则
故开路电压为
 |
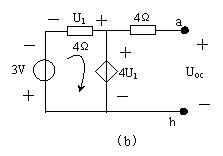再计算 a 、 b 二端网络的等效内阻。由于该二端网络内含有受控源，因此应采用外加电压法或短路电流法。我们先采用外加电压法计算，这时应把二端网络内的所有独立源都取为 0 ，电路如图 4.3-4 （ c ）所示。
图 4.3-4 （ c ）中，有
则
故
所以，等效内阻为
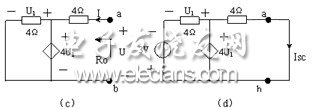
下面，采用短路电流法计算，这时应把二端网络内的所有独立源都保留，电路如图 4.3-4 （ d ）所示。图 4.3-4 （ d ）中，
则 
又
所以
等效内阻为
显然，这两种方法计算的结果是一样的。实际应用时，可根据具体情况选择一种方法。
3 ．戴维南等效电路如图 4.3-4 （ e ）所示。
由图 4.3-4 （ e ），得到 1V 电压源支路的电流为
所以， 1V 电压源吸收的功率为
 |
二、诺顿定理
诺顿定理
（ Norton theorem ）
对于一个线性的含源二端网络，对外电路而言，它可以用一个理想电流源和一个内阻相并联的电路来等效，称为诺顿等效模型。
其中，等效电流源的电流为该含源二端网络的短路电流 
，等效内阻为该含源二端网络中所有独立源都视为 0 时的等效电阻 
。
