第 4 节 最大功率传输定理
现在的问题是，当 Ns 已经给定时，负载获得最大功率的条件，即负载为何值时获得最大功率？最大功率又是多少？
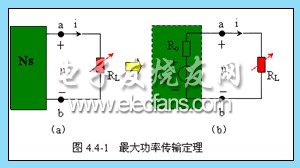
图 4.4-1 （ b ）中，流过负载 RL 的的电流为
则负载获得的功率为
令 
，得
这时，得功率的最大值为
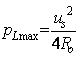
最大功率传输定理：一个含源二端网络对负载电阻供电，当负载电阻 RL 与该含源二端网络的等效内阻 
相等时，负载电阻上获得最大功率，且最大功率为 
。
称为最大功率匹配条件。
注 意：当负载获得最大功率时， 
，则电源的内阻消耗的功率与负载获得的功率是相等的，都是 
，也就是说，电源放出的功率有一半浪费在自己本身的内阻上了。因此，这时的效率只为 50% 。实际电路系统中一般不希望出现这种情况，往往要采用其他办法来提高效率。
例 4.4-1 图 4.4-2 （ a ）所示电路， R 是可调电阻，欲使 2 Ω电阻获得最大功率，求可调电阻 R 应调到何值，并求 2 Ω电阻获得的最大功率。
 |
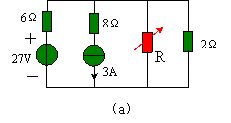解：将 2 Ω电阻左侧电路看成一个含源二端网络，求它的戴维南等效模型。
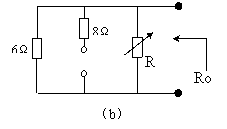
1 ．先求该含源二端网络的等效内阻 Ro ，电路如图 4.4-2 （ b ）所示，这时，等效内阻是 R 与
6 Ω并联，即
由最大功率的匹配条件，当 Ro=2 Ω时， 2 Ω电阻可以获得最大功率，即
解得，
这时该含源二端网络的等效内阻为
 |
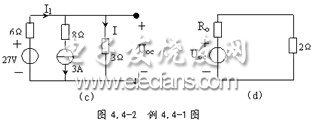
2 ．再求该含源二端网络的开路电压 Uoc ，电路如图 4.4-2 （ c ）所示，
解得，
所以，开路电压为
3 ．用戴维南等效模型替换后的电路如图 4.4-2 （ d ）所示， Uoc=3V ， Ro=2 Ω。因此，欲使 2 Ω电阻获得最大功率，可调电阻应为 
，这时 2 Ω电阻获得的最大功率为
