第 2 节 动态电路及初始状态
一、动态电路
动态电路（ dynamic circuits ）
动态元件具有动态性、记忆性和储能性等特点，含有动态元件的电路叫动态电路。
含有一个独立动态元件的电路称为一阶动态元件，电路方程是一阶微分方程；含有两个独立动态元件的电路称为二阶动态元件，电路方程是二阶微分方程。
图 5.2-1 所示电路中， LP1 、 LP2 和 LP3 是三个白炽灯，它们分别与电阻 R 、电容 C 和电感 L 相串联，并通过开关 S 接到直流电压源 Us 上，开关 S 闭合之前，三个灯泡都不亮。
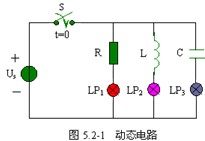
t=0 时开关 K 闭合，观察现象
1 、与电阻 R 串联的灯泡 LP1 立即发光，且亮度始终保持不变；
2 、与电感 L 串联的灯泡 LP2 开始并不发光，过一会才慢慢变亮，直至亮度达到最亮，且一直保持不变；
3 、与电容 C 串联的灯泡 LP3 立即发光，但稍后开始慢慢变暗，直至最后熄灭。
二、初始状态
1 、换路定则
换 路（ switching ）
动态电路中，把某一时刻电源或无源元件的接入、断开、某些支路的短路或开路及某些元件参数的改变称为电路换路，而且认为换路是在即刻完成的。
电路换路，使得电路改变原来的稳定状态，进入暂态（ transient state ）过程或过渡过程。当暂态过程结束后，电路又会达到新的稳定状态，简称稳态（ steady state ）。
换路定则
电容电压在换路瞬间不能跃变
电感电流在换路瞬间不能跃变
是换路前的一瞬间， 
是换路后的一瞬间。
注 意
电路中其它响应，如电容电流 
、电感电压 
、电阻电压 
、电阻电流 
等，都不受换路定则的约束，都有可能发生跃变。
2 、初始值的计算
初始值的计算步骤
1 、画出 t=0 －时刻的等效电路，此时电路处于稳态。对于直流激励，将电容视为开路，将电感视为短路，求出 
和 
。
2 、由换路定则求 t=0 ＋时刻的电路初始状态，
3 、根据替代定理，用电压为 
的电压源和电流为 
的电流源替代电路中的电容和电感，作出 t=0 ＋时刻的等效电路，再按直流电阻电路的计算方法求出其它响应的初始值。
例 5.2-1 图 5.2-2 （ a ）所示电路中，已知 
时开关 S 处于断开状态，且电路已处于稳态。 t=0 时刻开关 S 闭合，求 t=0 ＋时刻的 
、 
、 
、 
、 
。
解： 1. 
时电路已处于稳态，由于 12V 直流电压源激励，根据电容、电感的性质，可将电容视为开路，将电感视为短路，且开关 S 断开，作出 t=0 －时刻的等效电路，如图 5.2-2 （ b ）所示。由图 5.2-2 （ b ）可知，
2 ．由换路定则得，
3 ． t=0 ＋时刻，由替代定理，用 4V 电压源替代电容 C ，用 1A 的电流源替代电感 L ，且此时开关 S 闭合，得 t=0 ＋时刻的等效电路，如图 5.2-2 （ c ）所示。
由图 5.2-2 （ c ）得
又
则
所以，各初始值为