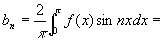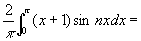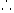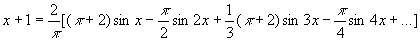10.4.1 函数展开成富里叶级数
定义：设周期为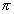
的函数f(x)在[-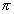,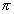]可积和绝对可积
令a
=
，
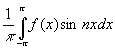n=1,2,3...，则称
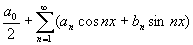是f(x)的富里叶级数记作
~
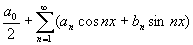
如果f(x)是周期为2l的函数在[-l,l]可积和绝对可积，则其富里叶级数为~
其中
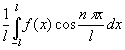
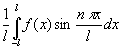n=1,2,3....
特殊的
(i)若f(x)为偶函数，则有
~
，
其中
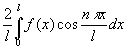n=1,2,3...
(ii)若f(x)为奇函数，则有
~
,
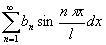其中
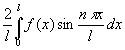n=1,2,3...
例：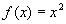
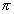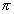在[-,]上展开成富里叶级数
解：因为f(x)为偶函数
所以富里叶系数
,
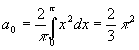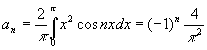
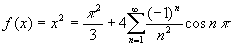
10.4.2 函数展开成正弦级数或余弦级数
在实际应用中,有时需要把定义在区间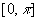
上的函数f(x)展开成正弦级数或余弦级数.根据上一节的知识,我们可以得到一下解决方法:
在开区间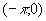
内补充函数f(x)的定义,得到定义在
上的函数F(x),使得它在
上成为奇函数(偶函数).按这种方法扩展函数定义域的过程成为奇延拓(偶延拓).然后用上一节的方法就可以得到函数富里叶级数.限制x在上,此时F(x)=f(x),这样便得到f(x)的正弦级数(余弦级数)展开式.
例:将函数f(x)=x+1(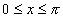
)展开城正弦级数
解:对函数f(x)进行奇延拓.
F(x)=f(x) (
)
F(x)=-f(-x) 
(
)
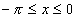