1. 函数相等
F1=f1(X0,……Xn-1) 若F1F2的输入变量均相等,而且变量的所有输入组合
F2=f2(X0,……Xn-1) 均有相等的输出取值,则F1=F2
举例:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 基本定律 | 加 | 乘 | ||||||||||||||||||||||||||||||||
| 0-1律 | A+0=A | A˙0=0 | ||||||||||||||||||||||||||||||||
| A+1=1 | A˙0=A | |||||||||||||||||||||||||||||||||
| A+A=A | A˙A=A | |||||||||||||||||||||||||||||||||
| A+Ā=1 | AĀ=0 | |||||||||||||||||||||||||||||||||
| 符合律 | (A+B)+C=A+(B+C) | (AB)C=A(BC) | ||||||||||||||||||||||||||||||||
| 交换律 | A+B=B+A | AB=BA | ||||||||||||||||||||||||||||||||
| 分配律 | A(B+C)=AB+AC | A+BC=(A+B)(A+C) | ||||||||||||||||||||||||||||||||
|
摩根定律 (反演律) |
|
|
||||||||||||||||||||||||||||||||
| 吸收律 |
A+AB=A A(A+B)=A (A+B)(A+C)=A+BC A+ĀB=A+B |
|||||||||||||||||||||||||||||||||
| 常用恒等式 | AB+C+BC=AB+ĀC AB+Ā C+BCD=AB+ĀC | |||||||||||||||||||||||||||||||||
|
注:这些公式反映了逻辑关系,而不是数量之间的关系,在运算中不能简单的用初等代数的运算规则。 如:初等代数中的移项规则不能用,这是因为逻辑代数中没有减法和除法的缘故。 |
||||||||||||||||||||||||||||||||||
3.三个变化规则
(1) 代入规则 等式两边同一变量以相同运算替换 等式不变
等式两边相同运算用同一变量代替
| __________ | |||||||||
| _ | _ | _ | _ | ||||||
| A | B | + | B | A | = | AB | + | A | B |
(2)对偶规则 表达式(等式)如果把式中:
|
+
|
 |
× |
|
×
|
 |
+ |
|
0
|
 |
1 |
|
1
|
 |
0 |
得到一个新的表达式(等式)称原表达式的对偶式.
|
|
|
|
||||||||||||||||||||||||
注意:1)保持原式运算次序
2)非号下面有两个或两个以上变量运算时,非号保留,非号下按规则变换
3)为了证明 F1=F2 可化成F1',F2' 证 F1'=F2'
__
(3)反演规则有F求F
|
+
|
 |
× |
|
×
|
 |
+ |
|
0
|
 |
1 |
|
1
|
 |
0 |
上式中:
|
|
|||||||||||||||||||||||||
|
注意:原
 反,反 反,反 原 原 |
注意: 对偶原则,反演原则都要注意保持先与后或的顺序
补充: 符合逻辑运算
若干基本逻辑运算的组合
| __ | |
|
1.与非运算F=
|
AB(见低出高,全高出低) |
|
 |
|
__
|
|
|
2. 或非运算 F=
|
A+B (见高出低,全低出高)
|
|
 |
3.与或非运算 F=AB+CD

|
_
|
_ |
_
|
|
|
4.异或运算 F=A
|
B+A
|
B=A⊕B特性: |
A⊕1=A,A⊕0=A
|
|
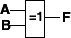 |
|
__
|
_ | |
|
5.同或运算 (符号运算) F=AB
|
+AB=A⊙B 特性: A⊙1=A , |
A⊙0=A
|
|
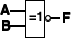 |
