2.1.1 逻辑变量与逻辑函数
与普通代数一样逻辑代数中的变量也用英文字母A，B，C,…等来表示，称为逻辑变量，逻辑变量的含义与普通代数情况完全不同，它们之间有着本质的区别，逻辑变量的取值只有两种可能：0或1，而且没有中间值，0和1并不表示数量的大小，而是表示两种对立的状态。按照逻辑学中的因果关系，某件事情的发生（结果）必然要具备其发生的条件（原因），这里可以约定1表示条件具备或事件发生，0表示条件不具备或事件不发生；相反也可以约定1表示条件不具备或事件不发生，0表示条件具备或事件发生。
如图2.1.1所示的电灯开关电路中，电灯是否点亮（结果）取决于开关是否接通（条件）。若定义Y＝1表示灯点亮，Y＝0表示灯熄灭；那么可以用A＝1表示开关闭合，A＝0表示开关断开。由于Y与A都是取值为1或为0的逻辑变量，并且开关的逻辑状态决定了电灯的逻辑状态，因此Y是A的函数，其函数表达式可写为Y＝f（A），逻辑变量A的取值决定了逻辑函数Y的结果。一般来说，一个逻辑函数中应包含多个逻辑变量，逻辑函数可表示为Y＝f（A，B，C，…），表达式由逻辑变量A，B，C，…和逻辑运算符等组成。逻辑运算符是逻辑运算关系中特定的符号，逻辑代数中最基本的逻辑运算有与、或、非三种，每种运算代表一种函数关系，这种函数关系可用逻辑符号写成逻辑表达式形式来描述，亦可以用文字来描述，还可以用表格或图形的方式来描述。
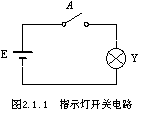
2.1.2 基本逻辑运算
人们常用因果关系来描述客观事物条件与结果之间的关系。在逻辑代数中,最基本的逻辑关系有三种,即与逻辑关系、或逻辑关系、非逻辑关系。下面通过几个具体的例子来描述这三种基本的逻辑关系。
一、与逻辑
如图2.1.2所示，A、B两串联开关控制电灯Y，开关A、B的状态组合有四种，这四种不同的状态组合与电灯点亮与熄灭之间的关系如表2.1.1所示。
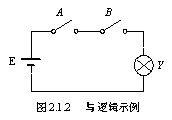
从表中可以看出，只有当开关A、B同时闭合时，电灯Y才会点亮；否则处于熄灭的状态。现在用1来表示条件具备或事件发生，即用1来表示开关闭合及灯亮；用0来表示条件不具备或事件不发生，即用0来表示开关断开及灯灭。因此表2.1.1所示的逻辑关系可以表示为表2.1.2所示的形式。这种把输入逻辑变量的所有取值组合及其相对应的输出结果列成的表格称之为真值表。从表2.1.1中可以得到如下的因果关系：只有当决定某一事件的条件（如开关闭合）全部具备时，这一事件（如灯亮）才会发生。这种因果关系称之为与逻辑关系。根据表2.1.2所示输出逻辑变量（逻辑函数）及输入逻辑变量的关系，这种与逻辑关系可以写成如下的逻辑函数表达式
Y=A·B （2.1.1）
式中：A与B为输入逻辑变量，即自变量；Y为输出逻辑变量，即因变量。式中的与运算符号“·”在不至于混淆的情况下，一般可以省略。与运算的意义为：只有当A和B都为1时，函数值Y才为1。读者很容易推广到三个（或三个以上）输入变量的情况。
由与逻辑关系的真值表可知与逻辑运算的运算规律为
0·0＝0
0·1＝1·0＝0
1·1＝1
简单的记为：“有0出0，全1出1”。
由此推出一般形式
A·0＝0 （2.1.2）
A·1＝A （2.1.3）
A·A＝A （2.1.4）
二、或逻辑
将图2.1.2所示电路稍作改变，把两个串联开关改为两并联开关控制电灯，电路如图2.1.3所示。两并联开关也有四种不同的状态组合，这些状态组合与灯亮、灯灭之间的关系如表2.1.3所示。同样用1表示条件具备或事件发生，0表示条件不具备或事件不发生，及1表示开关闭合、灯亮，0表示开关断开、灯灭，可以得到如表2.1.4所示的真值表。从其逻辑状态表中可以得到这样的因果关系：只有在决定某一事件（如灯亮）的各种条件中，有一个或几个条件（如开关闭合）具备时，这一事件就会发生。这种因果关系称之为或逻辑关系。
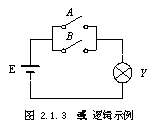
上述这种或逻辑关系可以写成如下的逻辑函数表达式
Y=A＋B （2.1.5）
式中“＋”为或逻辑运算符号。或运算的意义为：A或B只要有一个为1，则函数值Y为1。
由或逻辑关系的真值表可知或逻辑运算的运算规律为
0＋0=0
0＋1=1＋0=1
1＋1=1
简单的记为：“有1出1，全0出0”。
由此推出一般形式：
A＋0=A （2.1.6）
A＋1=1 （2.1.7）
A＋A=A （2.1.8）
三、非逻辑
如图2.1.4所示的开关电路中，开关A闭合时，灯亮；开关A断开时，灯灭。若用1表示开关闭合及灯亮，0表示开关断开及灯灭，可得逻辑真值表如表2.1.5所示。从其逻辑状态表中得到的因果关系如下：决定某一事件发生的条件（如开关闭合）具备时，事件（如灯亮）不发生；而当事件发生的条件不具备时，事件发生。这种因果关系称之为非逻辑关系。
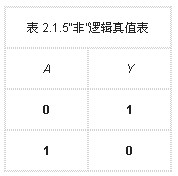
上述这种非逻辑关系可写成如下逻辑函数表达式
（2.1.9）
（2.1.9）式右边读作“A非”或“非A”。其中“¯”为非逻辑的逻辑运算符号。非运算的意义为：逻辑函数值为输入逻辑变量的反。
由非逻辑关系的真值表可知非逻辑的运算规律为：
简单的记为：“有0出1，有1出0”。
由此推出其一般形式
（2.1.10）
（2.1.11）
＝0 （2.1.12）
2.1.3 复合逻辑运算
实际数字系统中遇到的逻辑关系问题往往要比简单的与、或、非逻辑关系复杂得多，但是它们可以通过与、或、非的不同组合来实现，从而进行一些复合逻辑运算。常见的复合逻辑有：与非逻辑、或非逻辑、与或非逻辑、同或逻辑、异或逻辑等。
一、与非逻辑
与非逻辑实际上是与逻辑与和逻辑非的复合，它首先将输入变量进行与运算，然后再进行非运算。对于一个二输入逻辑变量的与非逻辑来说，其逻辑函数表达式为
（2.1.13）
与非逻辑的真值表如表2.1.6所示。
|
表 2.1.6 “与非”逻辑真值表 |
||
|
A |
B |
Y |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
二、或非逻辑
或非逻辑实际上是或逻辑和非逻辑的组合，它首先将输入变量进行或运算，然后再进行非运算。对于一个二输入逻辑变量的或非逻辑来说，其逻辑函数表达式为
（2.1.14）
|
表 2.1.7 “或非”逻辑真值表 |
||
|
A |
B |
Y |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
或非逻辑的真值表如表2.1.7所示。
|
表 2.1.8 “与或非”逻辑真值表 |
||||
|
A |
B |
C |
D |
Y |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
三、与或非逻辑
与或非逻辑是由与逻辑、或逻辑、非逻辑组合而成的，它首先将输入逻辑变量进行与运算，然后再进行或运算，最终进行非运算。对于一个2－2输入逻辑变量的与或非逻辑来说，其逻辑函数表达式为：
（2.1.15）
与或非逻辑的真值表如表2.1.8所示。
四、同或逻辑与异或逻辑
同或逻辑与异或逻辑都是只有两个输入逻辑变量的函数。
当两个输入逻辑变量取值相同时，输出逻辑函数值为1；两个输入逻辑变量取值不同时，输出逻辑函数值为0。这种逻辑关系称之为“同或”逻辑。其逻辑函数表达式为
＝⊙
＝
＋
（2.1.16）
式中：“⊙”为同或逻辑的运算符号。
|
表 2.1.9 “同或”逻辑真值表 |
||
|
A |
B |
Y=A⊙B |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
同或逻辑的真值表如表2.1.9所示。
由同或逻辑的真值表可知同或运算的规律为
0⊙0=1
0⊙1=1⊙0=0
1⊙1=1
简单的记为：“相同为1，相异为0”。
由此推出一般形式
⊙0= （2.1.17）
⊙1= （2.1.18）
⊙=0 （2.1.19）
⊙=1 （2.1.20）
与同或逻辑相反，当两个输入逻辑变量的取值相异时，输出逻辑函数值为1；两个输入逻辑变量取值相同时，输出逻辑函数值为0。这种逻辑关系称之为异或逻辑关系。其逻辑函数表达式为
（2.1.21）
式中“
”为异或逻辑的运算符号。
异或逻辑的真值表如表2.1.10所示。
|
表2.1.10“异或”逻辑真值表 |
||
|
A |
B |
Y=AÅB |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
由异或逻辑的真值表可知异或运算的规律为
简单的记为：“相同为0，相异为1”。
由此推出一般形式
（2.1.22）
（2.1.23）
（2.1.24）
（2.1.25）
2.1.4逻辑函数与真值表
在实际逻辑问题中。前面介绍的的基本运算和复合运算是很少单独出现，往往是构成各种复杂逻辑运算的基本单元，逻辑代数中的函数与普通代数中函数定义相类似，一个多变量输入的逻辑函数Y＝f（A，B，C，…），函数表达式由逻辑变量A，B，C，…和运算符号“+”，“ˉ”，“·”来构成。但概念上与普通代数的函数有本质的区别，主要表现为：
（1）逻辑函数自身和逻辑变量的取值只有0和1两种可能。
（2）逻辑函数与变量之间的关系完全由与、或、非三种基本运算确定。
从数字电路的角度逻辑函数可按如下定义：
设逻辑电路的输入逻辑变量为A，B，C，…，逻辑电路的输出Y，当A，B，C，…的值确定后，则Y的值就被唯一地确定下来，那么Y被称为A，B，C，…的逻辑函数。
例如:
,就是一个逻辑函数表达式，其中
表示逻辑变量A与B的反变量，表述一个逻辑电路输出端Y与其输入逻辑变量A，B，C之间的关系。
一、逻辑函数的真值表
逻辑函数表达式是表示输出量与输入量之间逻辑关系的一种形式，在数字逻辑电路中用真值表来描述逻辑函数更能直观输出量和输入量之间的逻辑关系。用真值表描述逻辑函数的方法是一种表格表示法，由于一个逻辑变量只有0和1两种可能的取值，故n个逻辑变量一共有
种可能的组合。任何逻辑函数总和若干个逻辑变量相关的，有限的变量个数使得变量取值组合的总数必然是有限的，从而能够用穷举的方法来描述逻辑函数的功能。为了清晰，常用的方法是对一个函数求出所有输入变量取值下的函数值，用表格的形式记录下来，这种表格就称为真值表。换而言之，真值表是一种由逻辑变量的所有可能取值组合及其对应的逻辑函数值勤所构成的表格。
真值表由两部份组成，左边一栏列出变量的所有取值组合，为了不发生遗漏，通常各变量取值组合按二进制数码顺序列出；右边一栏为逻辑函数的值。
例如：一个三输入变量的逻辑函数为
，其真值勤表如表2.1.11所示。
|
表2.1.11逻辑函数 |
|||
|
A |
B |
C |
Y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
的真值表真值表是一种十分有用的逻辑性工具，在逻辑性问题分析与设计中，会经常用这一工具。
二、真值表的逻辑表达式
真值表的最大特点是可直观输出量和输入量之间的逻辑关系，在数字逻辑电路中经常应用真值表来分析电路的逻辑功能。用表格的形式描述逻辑函数有很明显的局限性，因而经常要把真值表描述的逻辑功能写成逻辑函数表达式的形式。由真值表写出逻辑函数表达式实际上是由逻辑函数列写真值表的一个逆过程。
表2.1.11所示真值表与逻辑函数表达式的关系分析如下：
逻辑函数表达式可改写为
当A、B、C的取值为011时，
，则
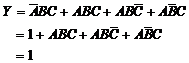
同理，在A、B、C的取值为111、110、101时，分别使
，
和
，使逻辑函数值为
。
因此，由真值表写出逻辑函数表达式时，首先把每个输出逻辑变量Y=1的相对应的一组输入变量（A、B、C、…）的组合状态以与项的形式表示，变量取值为1用原变量形式表示，变量取值为0用反变量形式表示；然后将所有使Y=1的与项进行逻辑或，便得到了输出Y的逻辑函数表达式，由于逻辑函数表达式Y中包含了所有使Y=1的输入组合，因此该表达式是完备的。
例2.1.1 列出下述逻辑问题的真值表，并写出描述该逻辑问题的逻辑函数表达式。
有A、B、C三个输入信号，当三个输入信号出现奇数个1时，输出Y为1；其余情况下，输出Y为0。
解 ：根据题意，当三个输入信号出现奇数个1时，输出为1，其余情况输出为0，得到8种不同取值组合的输出，真值表如表2.1.12所示。
从真值表中可见，输出Y＝1的输入变量取值组合为ABC＝001、010、100、111这四种，当
时，必然使得
；当
时，必然使得
；当A=1,B=0,C=0时，必然使得
；当A=B=C=1时，必然使得
，因此输出Y的逻辑函数应当等于这四个与项逻辑之和，即
|
表 2.1.12 奇数判断真值表 |
|||
|
A |
B |
C |
Y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
综上所述，一个逻辑函数表达式与表示该逻辑函数的真值表之间是可以相互转换的。
2.1.5 逻辑函数的相等
逻辑函数和普通代数中的函数一样存在相等的问题。假设有两个逻辑函数
（A1，A2，A3，…，An）
G（A1，A2，A3，…，An）
均为变量A1，A2，A3，…，An的逻辑函数，如果对应于变量A1，A2，A3，…，An的任意一组取值，Y与G的值都相等，则称Y和G是等值的，或者说Y和G是相等的，记作Y=G。
判断两个逻辑函数是否相等，通常有两种方法。一种方法是列出输入变量所有可能的取值组合，并按逻辑运算法则计算出各种输入取值下两个逻辑函数的相应值，然后进行比较。另一种方法是用逻辑代数的公理、定律和规则进行证明。