时序逻辑电路的分析，就是根据时序逻辑电路，得出该电路在时钟信号及输入信号的作用下，存储电路的状态转换关系及电路的输出结果，概括该电路的逻辑功能。分析时序逻辑电路一般采用存储电路的状态转移方程、输出逻辑函数表达式、状态转移表（图）及电压波形图等方法。

6.2.1同步时序逻辑电路的分析方法

同步时序逻辑电路的分析步骤可用图6.2.1所示框图来表示。

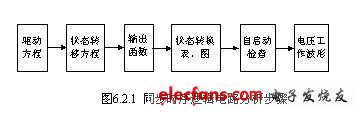
分析过程的具体步骤为：

(1) 根据逻辑电路写出各个触发器的驱动方程，即写出每个触发器输入端的逻辑函数表达式。

(2) 根据所给触发器，将得到的驱动方程代入触发器特性方程，得到时钟脉冲作用下的状态方程。

(3) 从逻辑电路中写出输出端的逻辑函数表达式。

(4) 将任何一组输入变量的取值及电路的初始状态，代入状态转移方程中和输出函数表达式中，得到时钟信号作用下的存储电路的次态逻辑值；再以得到的次态逻辑值为初始状态，和此时的输入变量的取值，再次代入状态转移方程中和输出函数表达式中，又得到新的次态逻辑值以及电路的输出值,如此循环代入逻辑值，直到所有输入变量的取值和所有逻辑状态值全部代入。将存储电路的状态转换以及电路的输出用表格的形式来描述它们之间的关系，称为状态转移表。将存储电路状态之间的转换关系用图形的方式来描述，就是状态转换图。

(5) 检查状态转换图(状态转移表)，如果在时钟信号和输入信号的作用下，各个状态之间能够建立联系，则说明该时序逻辑电路能够自启动，否则不能自启动。

(6) 根据状态转换表（图）来画触发器和输出端的时序图（即电压工作波形图）。

(7) 逻辑功能概述。

6.2.2同步时序逻辑电路的分析举例

下面通过例题来分析时序逻辑电路。

    例6.2.1 分析图6.2.2所示的同步时序逻辑电路。图中触发器由TTL门电路组成。

 
 

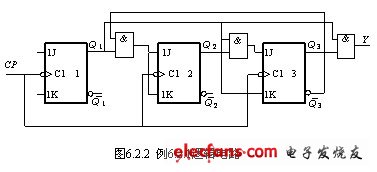
解：电路是由三个JK触发器组成的同步时序逻辑电路，电路中没有其他的输入信号，时钟信号是作为触发信号而作用在电路中的，属于下降沿触发。触发器的3个输出端为：Q₁、Q₂、Q₃，电路的输出端为Y。

    触发器1的J、K输入端悬空，由于题中的JK触发器是由TTL门电路组成，结合第三章TTL逻辑门的内部结构可知，在输入端悬空的情况下可视为高电平输入。所以可以得到该时序电路的驱动方程为：

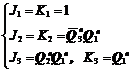                         （6.2.1）

代入式(5.3.1)JK触发器的状态方程：，可得电路的状态转移方程为：

                    （6.2.2）

输出端Y的表达式为：

                                                        （6.2.3）

上面得到的状态转移方程是在时钟信号的下降沿作用下的次态与初态的关系。从这些方程中我们并不容易看出逻辑状态间的转换关系，也不容易总结出其逻辑功能。在前面的章节中介绍了逻辑真值表，它反映的是逻辑电路中输入和输出的逻辑关系，也可以作出时序逻辑电路的真值表，可以把初态看作真值表中的输入量，次态看作真值表的输出量，这种真值表在这里叫做状态转移表。

根据这一方法，作状态转移表时，可以先假设初始状态为，在时钟信号的下降沿到来时，为计算次态的结果，须将初态值代入（6.2.2）式的状态转移方程中，得到次态结果为，再将得到的次态作为下一个时钟脉

冲下降沿作用时的初态，再次代入（6.2.2）式中，于是又得到一个新的次态结果，，依此类推的方法，得到一系列的次态值，记录在表6.2.1中。

表6.2.1  例6.2.1状态转移表
	时 钟 信 号	初     态	次     态	输    出
				Y
有 效 状 态	1 ↓ 2 ↓ 3 ↓ 4 ↓ 5 ↓ 6 ↓	0       0        0 0       0        1 0       1        0 0       1        1 1       0        0 1       0        1	0       0        1 0       1        0 0       1        1 1       0        0 1       0        1 0       0        0	0 0 0 0 0 1
偏 离状 态	1 ↓ 2 ↓	1       1        0 1       1        1	1       1        1 0       1        0	0 1

 

 

 

 

 

 

 

 

 

 

 

在表6.2.1中，表示出了时钟脉冲的下降沿作用下，所得到的次态值，也对应表示出了输出端Y的值。当第5个时钟脉冲下降沿作用时，得到触发器状态为，再来第6个时钟脉冲的下降沿，得到次态为，这样又回到了假设的初始状态，组成了时钟脉冲的循环计数，这6个状态的循环称为计数状态循环。电路中有3个触发器，其所有输出状态的组合应该有8种，6个循环状态之外的其他两种状态为110和111，这两种状态称为偏离状态。将初始状态代入式（6.2.2）中，可知两个时钟脉冲作用之后，仍然可以进入到计数循环中去。

从逻辑状态转换表中还不易直观的看出逻辑状态之间的转换关系，利用状态转换图可以更简洁明了的表示其状态转换关系。其状态转换图如图6.2.3所示。

在状态转换图中，表示出了触发器的所有状态之间的转换关系。同时也用斜线表示出了输入量和输出量之间的关系，输入量写在斜线的上面，输出量写在斜线的下面。在例6.2.1中，只有时钟信号输入，没有其他的输入量，所以在这个状态转换图中没有写出输入量。

根据状态转换表或状态转换图可以作出时钟脉冲作用下各个触发器的输出和电路输出端Y的电压波形图。作出例6.2.1中各触发器和输出信号的电压波形如图6.2.4所示。

 

 

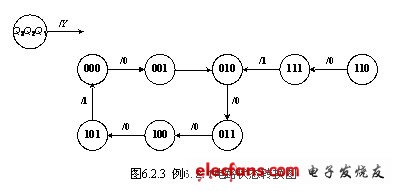
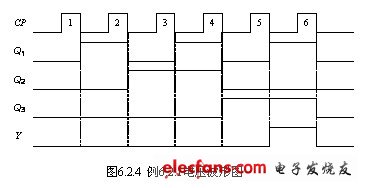
从前面得出的状态转换表、状态转换图和电压波形图可以看出，该逻辑电路是实现6逻辑状态的循环，是六进制计数器，输出端Y是进位输出端，每6个计数脉冲产生一个高电平进位信号，可以用于计数器的级联。偏离状态在时钟信号作用下也能够进入到计数循环中去，这说明电路具有自启动功能。也就是说，电路在受到外界干扰，使触发器的输出端的值为110或者111时，都可以进入到有效计数循环。这一功能提高了其抗干扰能力。

例6.2.2 分析图6.2.5所示的同步时序逻辑电路。

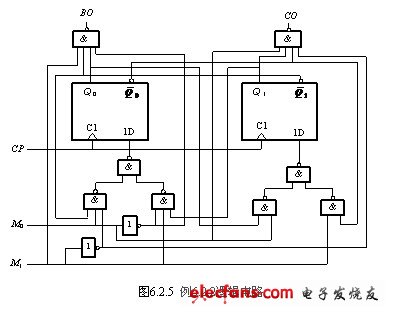
解：电路是由两个下降沿触发的D触发器组成的同步时序逻辑电路，电路中输入信号为M₀和M₁，触发器的两个输出端为Q₀和Q₁，电路的输出端为B_O和C_O。

从电路中可以得到该时序电路的驱动方程为：

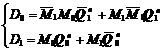                      （6.2.4）

代入式（5.4.1）D触发器的状态方程：，可得电路的状态转移方程为：

                 (6.2.5)
 

代入式（5.4.1）D触发器的状态方程：，可得电路的状态转移方程为：

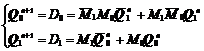                  (6.2.5)

输出端表达式为：

               ,                  (6.2.6)

对（6.2.5）式分析，根据输入信号M₁和M₀的控制作用，在时钟脉冲的上升沿作用下，触发器输出端Q₁和Q₀的次态方程可化简为：

，时，,；

，时，,；

，时，,；

，时，,；

根据上面的结果可以作出状态转换表，如表6.2.2所示。

根据状态表可以作出状态转换图，如图6.2.6所示。

图6.2.6中，状态循环之间的编码是采用循环码的计数编码方式。

表6.2.2  例6.2.2状态转换表
输	入	时 钟	初	态	次	态	输	出	功 能
M1	M0	CP					BO	CO
0 0 0 0	1 1 1 1	↑ ↑ ↑ ↑	0 0 1 1	0 1 1 0	0 1 1 0	1 1 0 0	1 1 1 1	1 1 1 0	加 计 数
1 1 1 1	0 0 0 0	↑ ↑ ↑ ↑	0 1 1 0	0 0 1 1	1 1 0 0	0 1 1 0	1 1 1 0	1 1 1 1	减 计 数
0	0	↑	×	×	0	0	1	1	置0
1	1	↑	×	×	1	0	1	1	置10

 

 

 

 

图6.2.6(a)为，时，触发器输出状态之间的转换情况，可见其计数循环为加计数；图6.2.6(b)为，时，触发器输出状态之间的转换情况，可见其计数循环为减计数；图6.2.6(c)为，时，触发器输出状态之间的转换情况，可见其功能是在时钟脉冲上升沿作用下，使触发器输出端置0；图6.2.6(d)为，时，触发器输出状态之间的转换情况，可见其功能是在时钟脉冲上升沿作用下，使触发器输出端Q₁Q₀置为10。

电路中的输出端CO只有在加计数循环中，触发器输出为10时才为0，所以CO是实现的是进位功能。电路中的输出端BO只有在减计数循环中，触发器输出为01时才为0，所以BO是实现的是借位功能。图6.2.7为该电路的电压波形图。

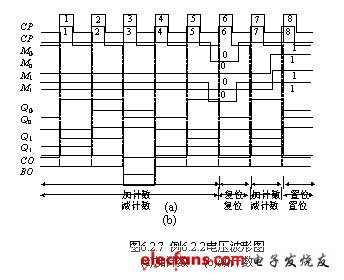
过上面的分析可知图6.2.5电路的逻辑功能是2位循环码加减计数器，M₁和M₀为工作模式控制，计数的复位（Q₁＝Q₀＝0）和置位（Q₁＝1，Q₀＝0）是在时钟脉冲作用下得到的，所以该计数器的复位和置位是与时钟同步的。BO为减计数借位端，CO为加计数进位端。