摘要
在机械臂抓取和操纵 3D 可变形物体时,必须考虑手指与物体之间的物理接触约束,以验证任务的稳定性。然而,以前的工作很少建立基于这些约束的接触相互作用模型,从而能够在抓取过程中精确控制力和变形。 本文考虑了可变形物体抓取过程的所有步骤,以通过计算初始接触点(预抓取策略)以及随后手指闭合时接触区域的接触力和局部变形来实现完整的抓取规划。可变形物体的行为使用非线性各向同性质量弹簧系统建模,该系统能够产生潜在变形。通过在仿真过程中结合两种模型(接触相互作用和物体变形),提出了一种新的抓取规划方法,以保证3D抓取可变形物体的稳定性。最后,用 Barrett 手(3 指)和 6-DOF 工业机械臂执行几个 3D 可变形物体的抓取实验。不仅会获得手+目标系统的最终稳定抓取策略,还会计算手臂+手接近策略(预抓取策略)。
1、规划抓取方法简介
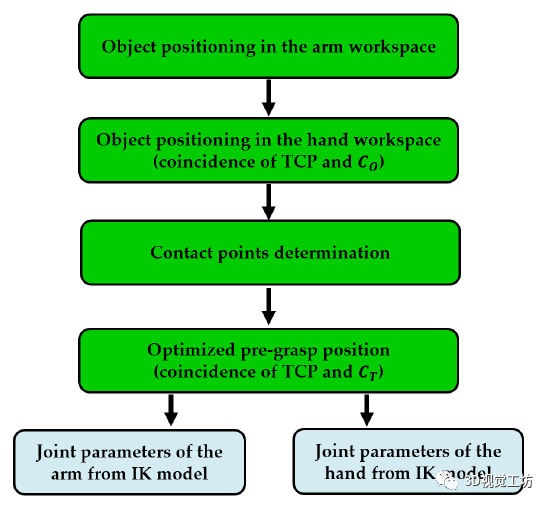
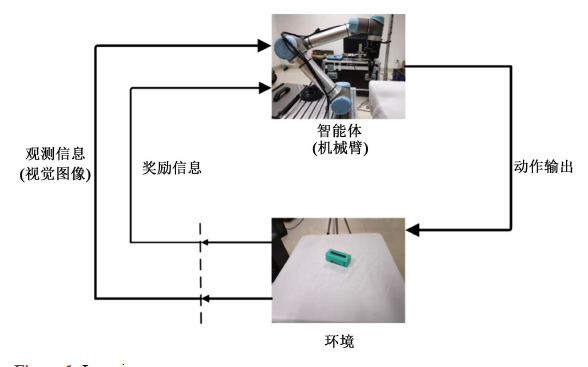
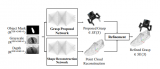
通过使用之前开发的接触模型,我们可以处理高度可变形的物体,并精确估计变形时产生的接触力。这些精确的估计将通过考虑新的抓握指标和优化机械手围绕物体的预抓握策略来保证物体的静态平衡。 图 1 中的流程图显示了计算和执行稳健抓取(即手指在物体表面的策略)所需的所有步骤,通过我们的抓取规划框架保证了物体的稳定性。
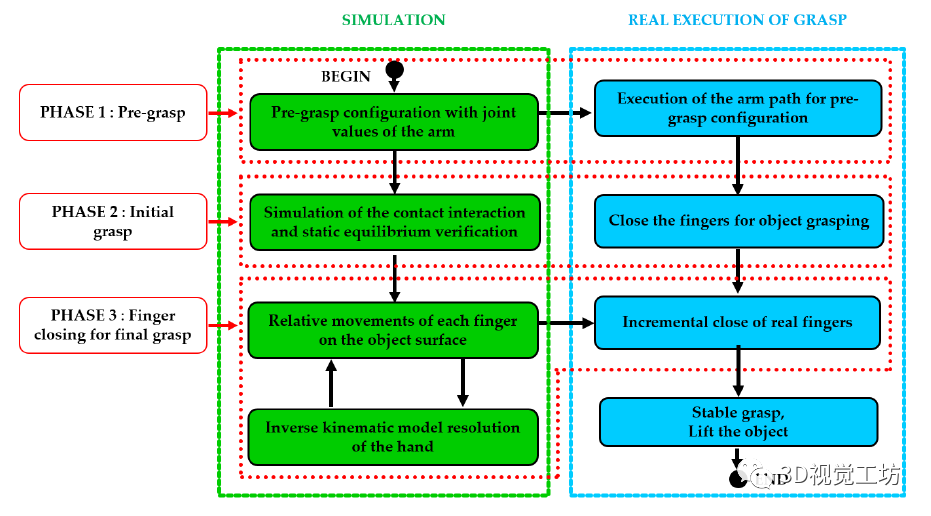
为了执行抓取计算,第一步确定预抓取策略。事实上,完整的抓取规划策略分为两个阶段:首先,确定机械臂的策略,使手靠近物体,手指可以到达物体表面。然后,根据新的几何标准确定手指的适当初始位姿以抓住物体。用于执行两个阶段的手臂和手的关节参数的确定通过其逆运动学 (IK) 的分辨率来保证。 一旦执行了预抓取,机器人就会移动到物体旁边,手指达到初始抓握位置。当手指接触到物体时,应该不会产生明显的变形,因为首先会施加一个很小的接触力,以避免抓握位置发生变化。一旦这个初始抓握被精确执行,算法的第三步就会被激活,手指的迭代闭合开始,基于接触交互模型的模拟。在模拟的每次迭代中,都会更新目标的形变并计算生成的接触力。计算出的接触力用于评估物体 + 手指系统的静态平衡。在仿真中重复迭代过程,直到达到静态平衡(参见图 1 中流程图左侧的仿真中的所有这些步骤)。 仿真过程完成后,可以通过执行从仿真中获得的接触力来执行对象的实际处理和操作(参见流程图右侧的步骤)。首先,将对象安装在机器人的工作区,其相对配置与仿真开始时相同。然后,机械臂向预抓位置(即现实中的第 1 阶段)移动,手指通过位置控制(即现实中的第 2 阶段)移向初始接触点。在此阶段(实际上是阶段 3 的开始),手指通过力控制闭合并逐渐挤压物体,直到接触力(由安装在 Barrett 手的每个手指内的接触传感器测量)等于在模拟步骤中计算的接触力。这些接触力保证了物体-手系统的平衡(通过模拟验证)。因此,物体可以从桌子上抬起没有任何滑动的风险,可以稳健地操纵。在接下来的部分中,将详细描述这些步骤,并通过对可变形物体进行真实的取放实验进行验证。
2、初始抓取策略
在本节中,我们将讨论三指抓取物体稳定性的特征。这意味着根据从表示对象外部 3D 表面的所有点集中选择的三个接触点来确定力闭合策略。此过程中考虑了以下假设: 1)使用三个手指进行抓取操作,建模为半径为 R 的半球 2)手指与物体的第一次接触是点接触 3)物体的外表面由一组点 表示,这些点由相对于物体质心 ( ) 的参考系测量的位置矢量 描述 事实上,当三指抓握收敛于理想的等边抓握时,在稳定性、防滑性和力平衡方面更可靠。因此,每个三指抓握都可以用一个值来表征,该值表示它与等边三角形的相似性。我们建议一种基于几何标准的算法来找到这种等边抓取。该算法首先通过扫描属于接触面 的点来确定所有可能的抓取三角形的集合。然后,使用Q1标准,把这些三角形的角度值(alpha、beta 和 lambda) 和(即,等边三角形的角度)进行比较,以便选择最接近等边三角形的部分:
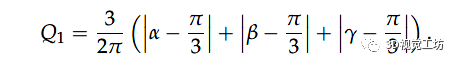
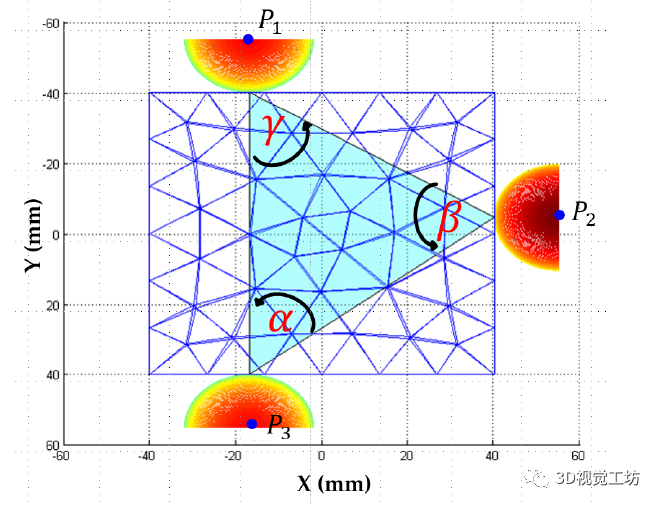
为了评估三角形的角度,我们使用由区间 [0, 0.3] 定义的误差范围。根据接触面 的点密度,该算法可以给出几种抓取配置。最后,使用第二个标准,称为 Q2,以便在它们之间选择一个。它测量物体 的质心与抓取三角形的中心 之间的距离,定义为 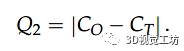
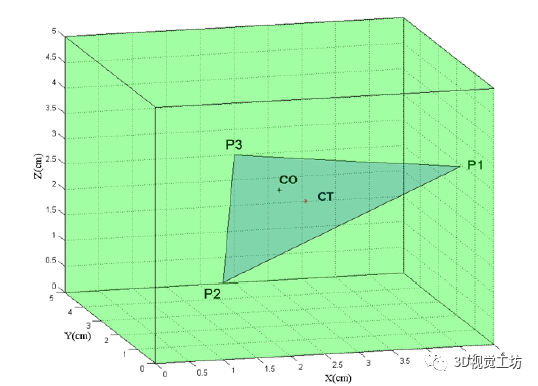
制定该标准是为了获得相对于重力和惯性力产生的扭矩的稳定抓握。基于这两个标准 Q1 和 Q2 的完整掌握合成算法在图表“算法 1”中表示:

3、机械手的预抓策略:手指的放置
三指机械手的预抓取策略包括两个步骤:第一步将手的方向与计算的初始抓取三角形对齐;第二步通过考虑手的运动学约束来调整对抓握的初始估计。第一步包括调整手的方向,使 TCP(工具中心点,沿垂直于手掌的轴定义)与 抓取三角形中心 重合。第二步涉及手指 IK 的分辨率,以估计关节值以达到初始抓取三角形的三个抓取点(、和 )。如果未找到 IK ,则更改 TCP 线的长度并重新计算 IK 分辨率。当找到 IK 时,通过应用的逆表达式计算电机命令 以关注这些关节值。实现的算法如图“算法 2”所示。在此迭代解决方案搜索的上下文中,我们认为该解决方案针对小于 2 度的每个手指的关节角度差值进行了验证。
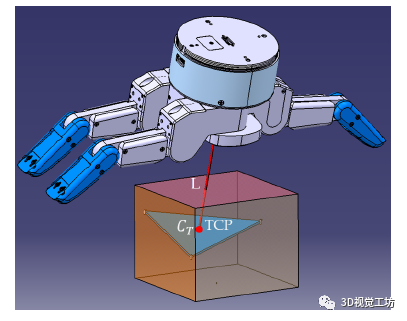

4、手 + 手臂系统的预抓策略:通过手臂实现轨迹移动
在建立手指的初始抓握点和手围绕物体的相应预抓握策略之后,我们应该通过用携带它的机械臂移动手来执行与抓取。下图显示了手 + 手臂系统的预抓策略流程图,该系统使用手臂和手的 IK 来实现初始抓握。为了实施这一规划策略,我们选择了一个 6 自由度机械臂(例如,用于我们真实实验的 Viper S1700D),以便手可以在物体周围的空间中获得任何姿势(位置 + 方向)。最初,目标放在桌子上,由平行于手臂底座的 XY 平面建模。
5、基于接触交互建模的稳定抓取
为了能够在手指闭合时评估实验中发生的所有力的平衡,需要一个指尖和物体接触的相互作用模型来精确确定抓取过程中力-形变间的关系。该模型将在没有任何形变的情况下接收物体的初始抓握作为输入。 在初步抓握之后,手指应反复靠近物体的中心,直到物体上的所有力达到平衡并执行稳定的抓握。为了计算这种平衡所需的指尖力,这种接触模型的模拟是通过几个连续的步骤来实现的。首先,检测手指与物体之间的接触;然后,计算接触力(通过评估手指和物体之间的相对速度)。最后,检查静态平衡以确保抓握稳定性。在模拟的每次迭代中,动态模型都会更新由于施加的力而导致的整体形状和接触区域变形。为每个接触点单独计算接触力,从而给出接触区域中接触压力的真实分布。接触模型考虑了法向力和摩擦引起的切向力的两种模式:滑动和粘附模式。由于对象由一组非线性弹簧 - 阻尼器对建模,因此非线性法向力由下式给出:
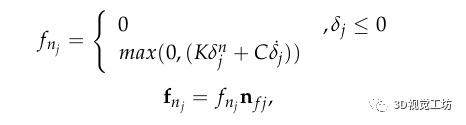
其中 是沿接触面 的法线方向测量的穿透距离; 和 分别是接触刚度和阻尼常数。 需要对沿每个触点作用的切向力进行建模,以防止任何滑动并确保抓握稳定性。接触模型考虑了摩擦引起的切向力的两种模式:滑动和粘附模式。在这个模型中,平行弹簧阻尼器的一端通过滑块元件连接到地面,另一端连接到指尖。因此,接触点位置在滑动条件下动态变化。这些变量分别对应于接触点处由于粘附和滑动引起的相对位移。如果接触断开,它们会动态重置为零。滑动摩擦力可以根据库仑定律定义如下:
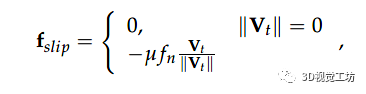
其中 、 和 分别是摩擦系数、法向力和切向速度。使用该模型,接触点位置在滑动条件下动态变化。如果切向力范数小于滑动阈值,则我们有一个粘附函数,其切向力定义为
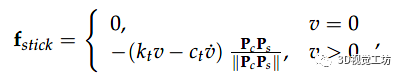
其中 是接触面上的切向变形, 是接触点位置, 是粘附状态下的接触点位置。参数 和 分别是使用 Dopico 方法估计的切向刚度和阻尼系数。 如本节开头所述,此接触模型将在达到初始抓取位置(作为预抓取策略的输出获得)并且手指开始接触物体表面后执行。事实上,在 Matlab 中实现了抓取执行策略的模拟,以确定应该施加的接触力以实现稳定抓取。该模拟将迭代地将手指靠近物体的中心,通过求解接触模型来评估传递给物体的力,更新由于变形导致的接触表面的状态,并验证手 + 物体系统的静态平衡。当在模拟中获得这种静态平衡时,模拟手指施加的接触力将作为真实机械手力控制的参考。
总结
本文致力于用工业机械手(机械手+机械臂)进行可变形物体抓取规划的完整过程。首先,这需要定义物体表面上的抓取点,从而确定初始抓取策略。然后,提出了通过考虑手臂和手的运动学约束。因此,抓取规划分为两个阶段,第一阶段,确定机器人手臂的策略,使手靠近物体;确定手指的适当策略以抓住物体, 手臂和手的关节参数的确定是由它们的逆运动学的分辨率来保证的。只考虑到手的情况下,实施的策略包括首先将 TCP(垂直于手掌的线)置于与抓握三角形中心(在初始抓握合成中获得)的交点处,并将其与法线对齐 这个抓取三角形的矢量。第二步是迭代搜索三个手指的关节参数的解决方案,以便使它们与先前由力闭合型稳定性条件定义的抓取点相对应。因此,该最终抓取方案通过应用所提出的预抓取策略,将基于力闭合的一般几何标准(即,它仅考虑物体的形状)的初始抓取与机械手的运动学约束相结合。然而,这种抓握策略确实只保证了刚性物体抓握的稳健性,而不能保证可变形物体的抓握稳健性。因此,当手指接触到要抓握的可变形物体时,就会激活力-形变方案。该方案基于物体与手指相互作用的模拟,它获得了手指应施加的接触力阈值,以确保在使物体表面变形时稳定抓握物体。最后,执行真实手指的迭代闭合以获得与真实物体的接触力。
审核编辑 :李倩
-
机器人
+关注
关注
212文章
29341浏览量
211106 -
3D
+关注
关注
9文章
2945浏览量
109242 -
机械臂
+关注
关注
13文章
542浏览量
25168
原文标题:一种使用工业机械臂稳定规划抓取 3D 可变形物体的方法
文章出处:【微信号:3D视觉工坊,微信公众号:3D视觉工坊】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
空间站机械臂抓取物体matlab代码实现设计
如何使用深度强化学习进行机械臂视觉抓取控制的优化方法概述
抓取作业机器人3D视觉系统的设计
机械臂路径规划方案的简单介绍
新一代双目结构光3D相机产品Gemini 2应用方案
myCobot Pro600六轴机械臂与3D深度视觉:物体精确识别抓取堆叠

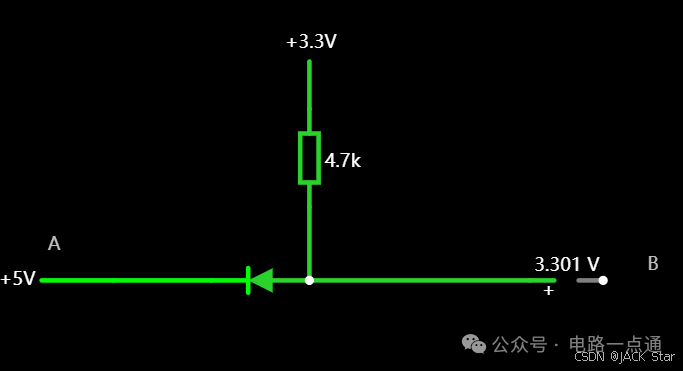
有几种电平转换电路,适用于不同的场景
一.起因一般在消费电路的元器件之间,不同的器件IO的电压是不同的,常规的有5V,3.3V,1.8V等。当器件的IO电压一样的时候,比如都是5V,都是3.3V,那么其之间可以直接通讯,比如拉中断,I2Cdata/clk脚双方直接通讯等。当器件的IO电压不一样的时候,就需要进行电平转换,不然无法实现高低电平的变化。二.电平转换电路常见的有几种电平转换电路,适用于

瑞萨RA8系列教程 | 基于 RASC 生成 Keil 工程
对于不习惯用 e2 studio 进行开发的同学,可以借助 RASC 生成 Keil 工程,然后在 Keil 环境下愉快的完成开发任务。

共赴之约 | 第二十七届中国北京国际科技产业博览会圆满落幕
作为第二十七届北京科博会的参展方,芯佰微有幸与800余家全球科技同仁共赴「科技引领创享未来」之约!文章来源:北京贸促5月11日下午,第二十七届中国北京国际科技产业博览会圆满落幕。本届北京科博会主题为“科技引领创享未来”,由北京市人民政府主办,北京市贸促会,北京市科委、中关村管委会,北京市经济和信息化局,北京市知识产权局和北辰集团共同承办。5万平方米的展览云集

道生物联与巍泰技术联合发布 RTK 无线定位系统:TurMass™ 技术与厘米级高精度定位的深度融合
道生物联与巍泰技术联合推出全新一代 RTK 无线定位系统——WTS-100(V3.0 RTK)。该系统以巍泰技术自主研发的 RTK(实时动态载波相位差分)高精度定位技术为核心,深度融合道生物联国产新兴窄带高并发 TurMass™ 无线通信技术,为室外大规模定位场景提供厘米级高精度、广覆盖、高并发、低功耗、低成本的一站式解决方案,助力行业智能化升级。

智能家居中的清凉“智”选,310V无刷吊扇驱动方案--其利天下
炎炎夏日,如何营造出清凉、舒适且节能的室内环境成为了大众关注的焦点。吊扇作为一种经典的家用电器,以其大风量、长寿命、低能耗等优势,依然是众多家庭的首选。而随着智能控制技术与无刷电机技术的不断进步,吊扇正朝着智能化、高效化、低噪化的方向发展。那么接下来小编将结合目前市面上的指标,详细为大家讲解其利天下有限公司推出的无刷吊扇驱动方案。▲其利天下无刷吊扇驱动方案一
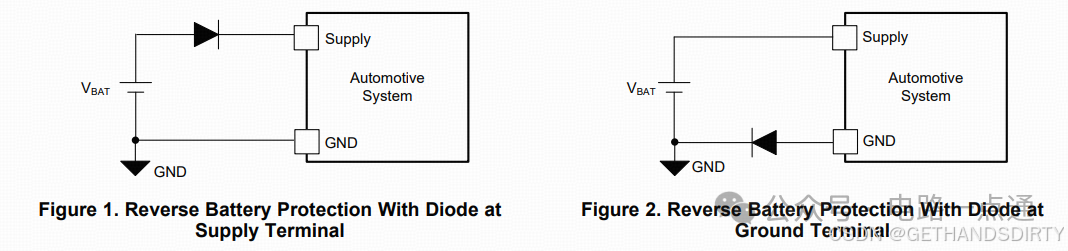
电源入口处防反接电路-汽车电子硬件电路设计
一、为什么要设计防反接电路电源入口处接线及线束制作一般人为操作,有正极和负极接反的可能性,可能会损坏电源和负载电路;汽车电子产品电性能测试标准ISO16750-2的4.7节包含了电压极性反接测试,汽车电子产品须通过该项测试。二、防反接电路设计1.基础版:二极管串联二极管是最简单的防反接电路,因为电源有电源路径(即正极)和返回路径(即负极,GND),那么用二极
半导体芯片需要做哪些测试
首先我们需要了解芯片制造环节做⼀款芯片最基本的环节是设计->流片->封装->测试,芯片成本构成⼀般为人力成本20%,流片40%,封装35%,测试5%(对于先进工艺,流片成本可能超过60%)。测试其实是芯片各个环节中最“便宜”的一步,在这个每家公司都喊着“CostDown”的激烈市场中,人力成本逐年攀升,晶圆厂和封装厂都在乙方市场中“叱咤风云”,唯独只有测试显

解决方案 | 芯佰微赋能示波器:高速ADC、USB控制器和RS232芯片——高性能示波器的秘密武器!
示波器解决方案总述:示波器是电子技术领域中不可或缺的精密测量仪器,通过直观的波形显示,将电信号随时间的变化转化为可视化图形,使复杂的电子现象变得清晰易懂。无论是在科研探索、工业检测还是通信领域,示波器都发挥着不可替代的作用,帮助工程师和技术人员深入剖析电信号的细节,精准定位问题所在,为创新与发展提供坚实的技术支撑。一、技术瓶颈亟待突破性能指标受限:受模拟前端
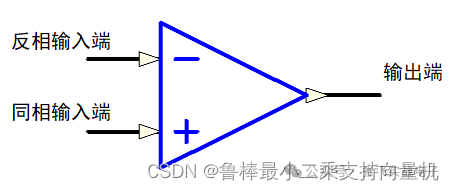
硬件设计基础----运算放大器
1什么是运算放大器运算放大器(运放)用于调节和放大模拟信号,运放是一个内含多级放大电路的集成器件,如图所示:左图为同相位,Vn端接地或稳定的电平,Vp端电平上升,则输出端Vo电平上升,Vp端电平下降,则输出端Vo电平下降;右图为反相位,Vp端接地或稳定的电平,Vn端电平上升,则输出端Vo电平下降,Vn端电平下降,则输出端Vo电平上升2运算放大器的性质理想运算

ElfBoard技术贴|如何调整eMMC存储分区
ELF 2开发板基于瑞芯微RK3588高性能处理器设计,拥有四核ARM Cortex-A76与四核ARM Cortex-A55的CPU架构,主频高达2.4GHz,内置6TOPS算力的NPU,这一设计让它能够轻松驾驭多种深度学习框架,高效处理各类复杂的AI任务。

米尔基于MYD-YG2LX系统启动时间优化应用笔记
1.概述MYD-YG2LX采用瑞萨RZ/G2L作为核心处理器,该处理器搭载双核Cortex-A55@1.2GHz+Cortex-M33@200MHz处理器,其内部集成高性能3D加速引擎Mail-G31GPU(500MHz)和视频处理单元(支持H.264硬件编解码),16位的DDR4-1600/DDR3L-1333内存控制器、千兆以太网控制器、USB、CAN、
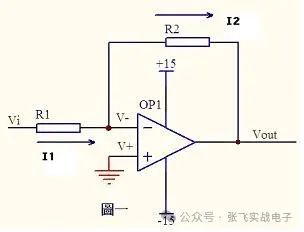
运放技术——基本电路分析
虚短和虚断的概念由于运放的电压放大倍数很大,一般通用型运算放大器的开环电压放大倍数都在80dB以上。而运放的输出电压是有限的,一般在10V~14V。因此运放的差模输入电压不足1mV,两输入端近似等电位,相当于“短路”。开环电压放大倍数越大,两输入端的电位越接近相等。“虚短”是指在分析运算放大器处于线性状态时,可把两输入端视为等电位,这一特性称为虚假短路,简称

飞凌嵌入式携手中移物联,谱写全国产化方案新生态
4月22日,飞凌嵌入式“2025嵌入式及边缘AI技术论坛”在深圳成功举办。中移物联网有限公司(以下简称“中移物联”)携OneOS操作系统与飞凌嵌入式共同推出的工业级核心板亮相会议展区,操作系统产品部高级专家严镭受邀作《OneOS工业操作系统——助力国产化智能制造》主题演讲。
ATA-2022B高压放大器在螺栓松动检测中的应用
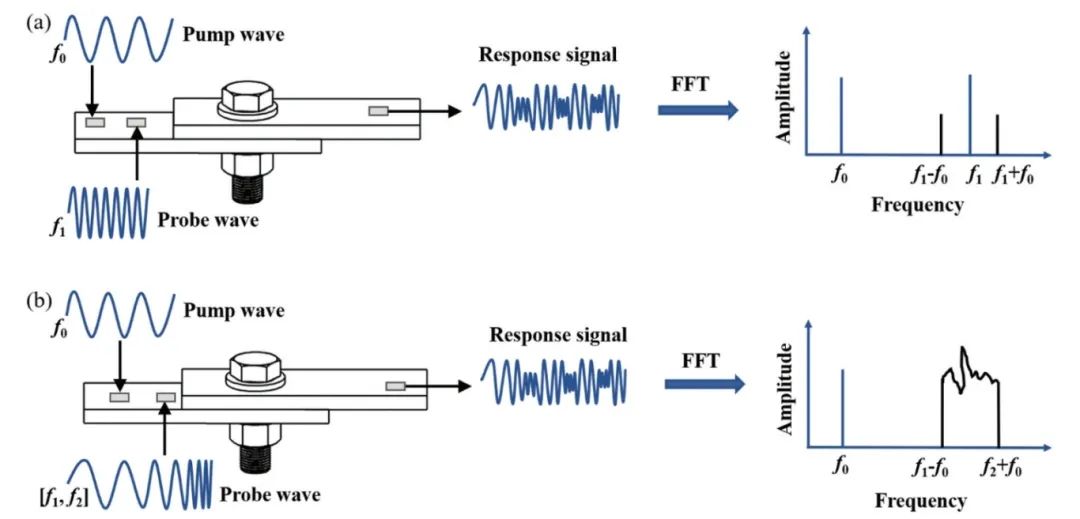
实验名称:ATA-2022B高压放大器在螺栓松动检测中的应用实验方向:超声检测实验设备:ATA-2022B高压放大器、函数信号发生器,压电陶瓷片,数据采集卡,示波器,PC等实验内容:本研究基于振动声调制的螺栓松动检测方法,其中低频泵浦波采用单频信号,而高频探测波采用扫频信号,利用泵浦波和探测波在接触面的振动声调制响应对螺栓的松动程度进行检测。通过螺栓松动检测
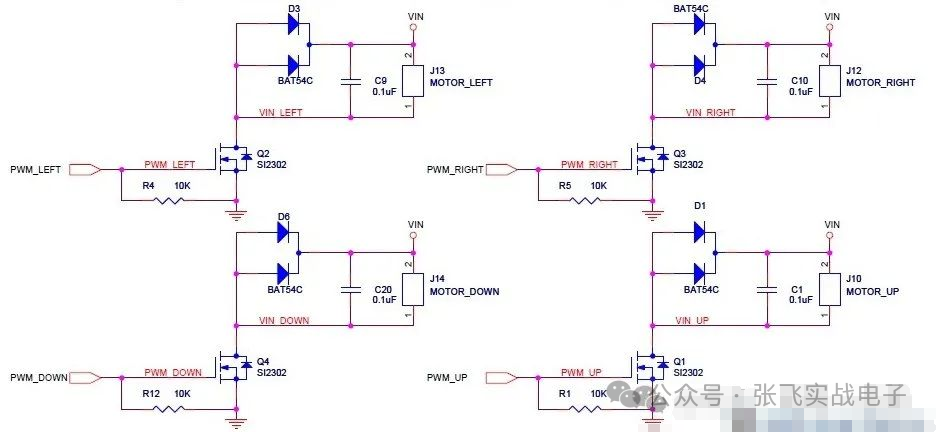
MOS管驱动电路——电机干扰与防护处理
此电路分主电路(完成功能)和保护功能电路。MOS管驱动相关知识:1、跟双极性晶体管相比,一般认为使MOS管导通不需要电流,只要GS电压(Vbe类似)高于一定的值,就可以了。MOS管和晶体管向比较c,b,e—–>d(漏),g(栅),s(源)。2、NMOS的特性,Vgs大于一定的值就会导通,适合用于源极接地时的情况(低端驱动),只要栅极电压达到4V或10V就可以





 一种使用工业机械臂稳定规划抓取3D可变形物体的方法
一种使用工业机械臂稳定规划抓取3D可变形物体的方法












评论