2.4.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( abs(pid.err)<= pid.umax )
{
index = 1 ;
pid.integral += pid.err ;
}
else
index = 0 ;
pid.voltage = pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<1000 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
printf( "%.2f\\n" , Speed ) ;
}
}
2.5 抗积分饱和型PID算法
2.5.1 实现原理
所谓积分饱和现象是指如果系统存在一个方向的偏差,PID控制器的输出会因为存在积分环节而不断累积增大,从而导致执行机构达到极限位置,若控制器输出响应继续增大,执行器开度不可能再增大,此时计算机输出控制量超出了正常运行范围而进入饱和区,一旦系统出现反向偏差,输出响应逐渐从饱和区退出,进入饱和区时间越长则退出饱和区的时间也就随之增加,这段时间里,执行机构仍然停留在极限位置而不能随着偏差方向立即作出相应的改变,造成控制性能恶化,这种现象称为积分饱和现象或积分失控现象。实现抗积分饱和算法的基本思路是计算系统的响应时,首先判断上一时刻的控制量是否超出了极限范围,如果超过上限,则只累计反向偏差,若低于下限,则只累计正向偏差,从而避免控制量长时间停留在饱和区。
2.5.2 MATLAB算法
clc
clear
%PID初始化
len = 180 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.1 ; %积分值
max = 400 ; %积分上限
min = -200 ; %积分下限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %误差累计
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral + Kd*(err_1-err_0); %位置型PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
MATLAB运行结果如下图所示。
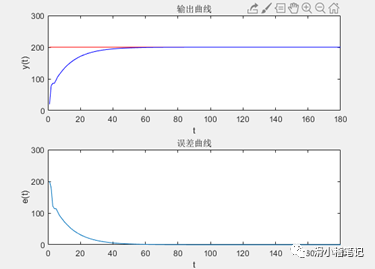
2.5.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
2.6 梯形积分PID算法
2.6.1 实现原理
根据梯形算法的积分环节公式
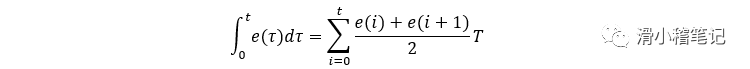
作为PID控制的积分项,其作用是消除余差,为了尽量减小余差,应提高积分项运算精度,为此可以将矩形积分改为梯形积分,具体实现的语句为pid.voltage = pid.Kppid.err+indexpid.Ki pid.integral/2+pid.Kd ( pid.err-pid.err_last ) ;
2.6.2 MATLAB算法
clc
clear
%PID初始化
len = 358 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.1 ; %积分值
max = 400 ; %积分上限
min = -200 ; %积分下限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %误差累计
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral/2 + Kd*(err_1-err_0); %PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
2.6.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
-
matlab
+关注
关注
188文章
2990浏览量
232925 -
直流电机
+关注
关注
36文章
1720浏览量
71220 -
PID
+关注
关注
37文章
1479浏览量
87053
发布评论请先 登录
PID算法之模糊PID 精选资料推荐
基于遗传算法的PID 控制及其MATLAB 仿真
MATLAB学习笔记之PID算法3


智能家居中的清凉“智”选,310V无刷吊扇驱动方案--其利天下
炎炎夏日,如何营造出清凉、舒适且节能的室内环境成为了大众关注的焦点。吊扇作为一种经典的家用电器,以其大风量、长寿命、低能耗等优势,依然是众多家庭的首选。而随着智能控制技术与无刷电机技术的不断进步,吊扇正朝着智能化、高效化、低噪化的方向发展。那么接下来小编将结合目前市面上的指标,详细为大家讲解其利天下有限公司推出的无刷吊扇驱动方案。▲其利天下无刷吊扇驱动方案一
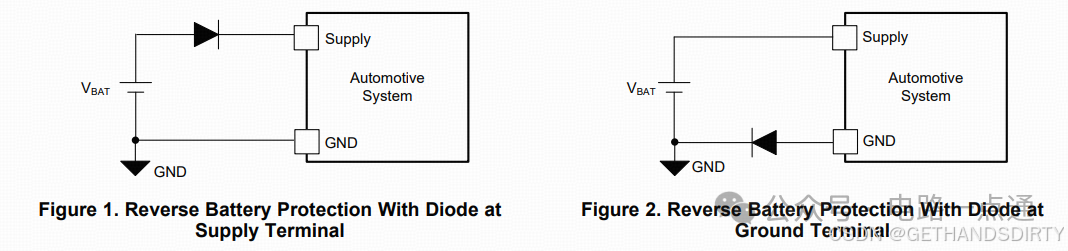
电源入口处防反接电路-汽车电子硬件电路设计
一、为什么要设计防反接电路电源入口处接线及线束制作一般人为操作,有正极和负极接反的可能性,可能会损坏电源和负载电路;汽车电子产品电性能测试标准ISO16750-2的4.7节包含了电压极性反接测试,汽车电子产品须通过该项测试。二、防反接电路设计1.基础版:二极管串联二极管是最简单的防反接电路,因为电源有电源路径(即正极)和返回路径(即负极,GND),那么用二极
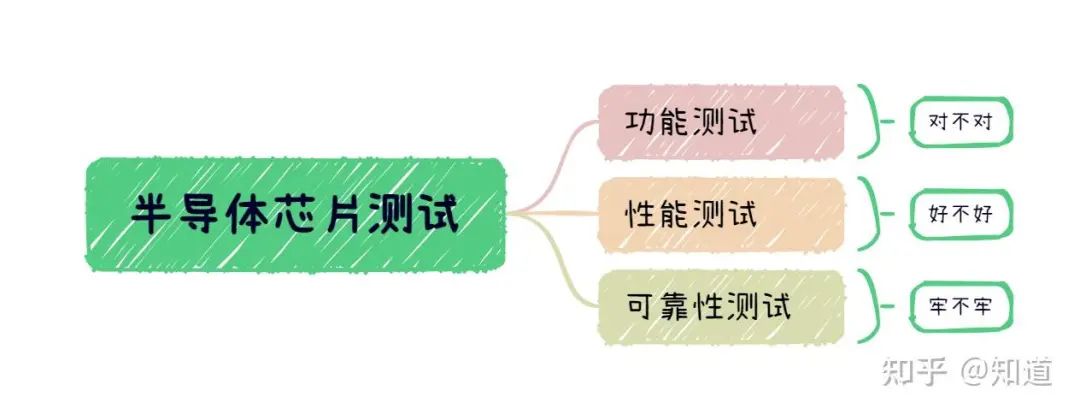
半导体芯片需要做哪些测试
首先我们需要了解芯片制造环节做⼀款芯片最基本的环节是设计->流片->封装->测试,芯片成本构成⼀般为人力成本20%,流片40%,封装35%,测试5%(对于先进工艺,流片成本可能超过60%)。测试其实是芯片各个环节中最“便宜”的一步,在这个每家公司都喊着“CostDown”的激烈市场中,人力成本逐年攀升,晶圆厂和封装厂都在乙方市场中“叱咤风云”,唯独只有测试显

解决方案 | 芯佰微赋能示波器:高速ADC、USB控制器和RS232芯片——高性能示波器的秘密武器!
示波器解决方案总述:示波器是电子技术领域中不可或缺的精密测量仪器,通过直观的波形显示,将电信号随时间的变化转化为可视化图形,使复杂的电子现象变得清晰易懂。无论是在科研探索、工业检测还是通信领域,示波器都发挥着不可替代的作用,帮助工程师和技术人员深入剖析电信号的细节,精准定位问题所在,为创新与发展提供坚实的技术支撑。一、技术瓶颈亟待突破性能指标受限:受模拟前端
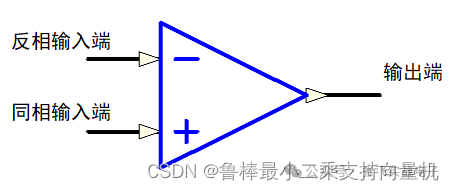
硬件设计基础----运算放大器
1什么是运算放大器运算放大器(运放)用于调节和放大模拟信号,运放是一个内含多级放大电路的集成器件,如图所示:左图为同相位,Vn端接地或稳定的电平,Vp端电平上升,则输出端Vo电平上升,Vp端电平下降,则输出端Vo电平下降;右图为反相位,Vp端接地或稳定的电平,Vn端电平上升,则输出端Vo电平下降,Vn端电平下降,则输出端Vo电平上升2运算放大器的性质理想运算

ElfBoard技术贴|如何调整eMMC存储分区
ELF 2开发板基于瑞芯微RK3588高性能处理器设计,拥有四核ARM Cortex-A76与四核ARM Cortex-A55的CPU架构,主频高达2.4GHz,内置6TOPS算力的NPU,这一设计让它能够轻松驾驭多种深度学习框架,高效处理各类复杂的AI任务。

米尔基于MYD-YG2LX系统启动时间优化应用笔记
1.概述MYD-YG2LX采用瑞萨RZ/G2L作为核心处理器,该处理器搭载双核Cortex-A55@1.2GHz+Cortex-M33@200MHz处理器,其内部集成高性能3D加速引擎Mail-G31GPU(500MHz)和视频处理单元(支持H.264硬件编解码),16位的DDR4-1600/DDR3L-1333内存控制器、千兆以太网控制器、USB、CAN、
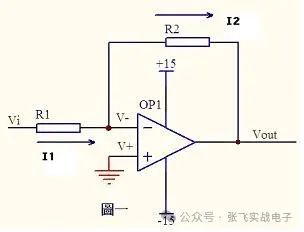
运放技术——基本电路分析
虚短和虚断的概念由于运放的电压放大倍数很大,一般通用型运算放大器的开环电压放大倍数都在80dB以上。而运放的输出电压是有限的,一般在10V~14V。因此运放的差模输入电压不足1mV,两输入端近似等电位,相当于“短路”。开环电压放大倍数越大,两输入端的电位越接近相等。“虚短”是指在分析运算放大器处于线性状态时,可把两输入端视为等电位,这一特性称为虚假短路,简称

飞凌嵌入式携手中移物联,谱写全国产化方案新生态
4月22日,飞凌嵌入式“2025嵌入式及边缘AI技术论坛”在深圳成功举办。中移物联网有限公司(以下简称“中移物联”)携OneOS操作系统与飞凌嵌入式共同推出的工业级核心板亮相会议展区,操作系统产品部高级专家严镭受邀作《OneOS工业操作系统——助力国产化智能制造》主题演讲。
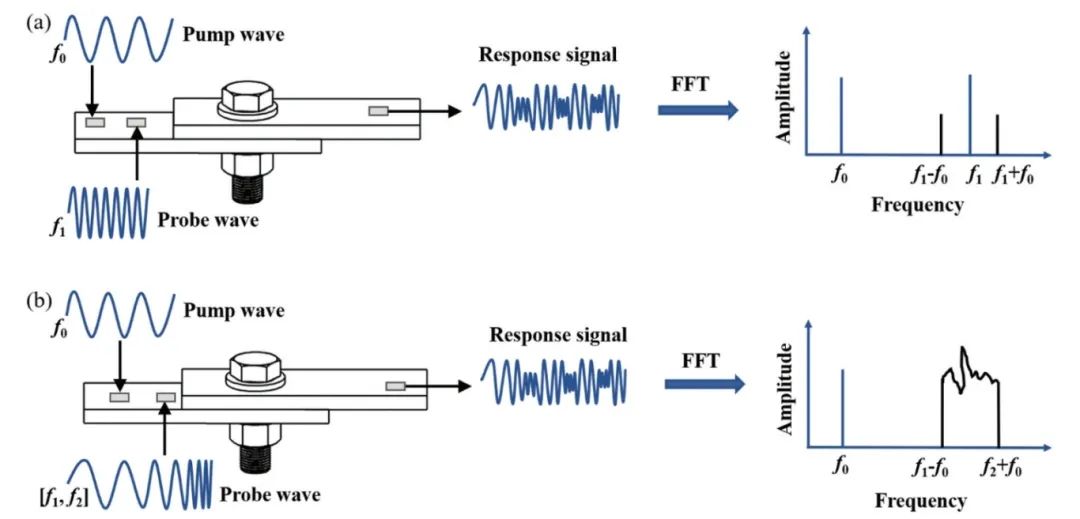
ATA-2022B高压放大器在螺栓松动检测中的应用
实验名称:ATA-2022B高压放大器在螺栓松动检测中的应用实验方向:超声检测实验设备:ATA-2022B高压放大器、函数信号发生器,压电陶瓷片,数据采集卡,示波器,PC等实验内容:本研究基于振动声调制的螺栓松动检测方法,其中低频泵浦波采用单频信号,而高频探测波采用扫频信号,利用泵浦波和探测波在接触面的振动声调制响应对螺栓的松动程度进行检测。通过螺栓松动检测
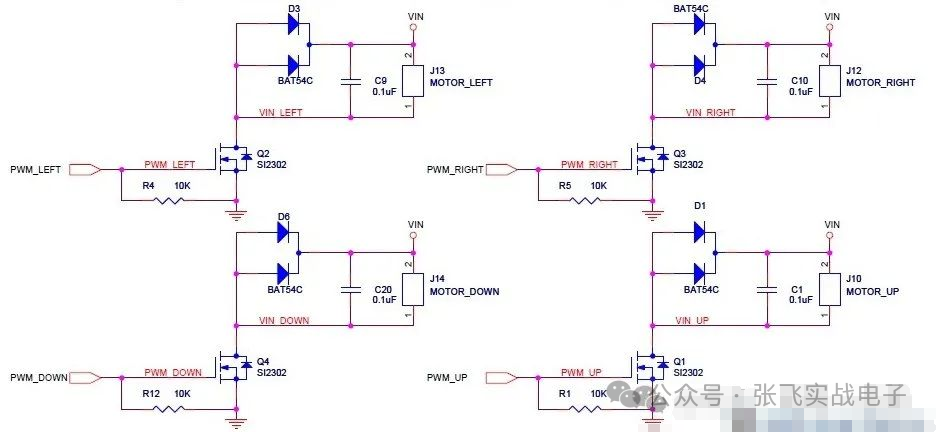
MOS管驱动电路——电机干扰与防护处理
此电路分主电路(完成功能)和保护功能电路。MOS管驱动相关知识:1、跟双极性晶体管相比,一般认为使MOS管导通不需要电流,只要GS电压(Vbe类似)高于一定的值,就可以了。MOS管和晶体管向比较c,b,e—–>d(漏),g(栅),s(源)。2、NMOS的特性,Vgs大于一定的值就会导通,适合用于源极接地时的情况(低端驱动),只要栅极电压达到4V或10V就可以
压敏(MOV)在电机上的应用剖析
一前言有刷直流电机是一种较为常见的直流电机。它的主要特点包括:1.结构相对简单,由定子、转子、电刷和换向器等组成;2.通过电刷与换向器的接触来实现电流的换向,从而使电枢绕组中的电流方向周期性改变,保证电机持续运转;3.具有调速性能较好等优点,可以通过改变电压等方式较为方便地调节转速。有刷直流电机在许多领域都有应用,比如一些电动工具、玩具、小型机械等。但它也存
硬件原理图学习笔记
这一个星期认真学习了硬件原理图的知识,做了一些笔记,方便以后查找。硬件原理图分为三类1.管脚类(gpio)和门电路类输入输出引脚,上拉电阻,三极管与门,或门,非门上拉电阻:正向标志作用,给悬空的引脚一个确定的状态三极管:反向三极管(gpio输出高电平,NP两端导通,被控制端导通,电压为0)->NPN正向三极管(gpio输出低电平,PN两端导通,被控制端导通,

TurMass™ vs LoRa:无线通讯模块的革命性突破
TurMass™凭借其高传输速率、强大并发能力、双向传输、超强抗干扰能力、超远传输距离、全国产技术、灵活组网方案以及便捷开发等八大优势,在无线通讯领域展现出强大的竞争力。

RZT2H CR52双核BOOT流程和例程代码分析
RZT2H是多核处理器,启动时,需要一个“主核”先启动,然后主核根据规则,加载和启动其他内核。本文以T2H内部的CR52双核为例,说明T2H多核启动流程。





 MATLAB学习笔记之PID算法2
MATLAB学习笔记之PID算法2












评论