上一篇文章介绍了一个电路,我称之为双运放电流源(或电流泵)。
这是原理图:

精密电流泵示意图。图片由Analog Devices提供
我展示了此拓扑的LTspice实现,我们查看了基本模拟的结果。不过,我想了解更多有关此电路的信息,尤其是因为它被描述为精密电流泵。我们真正期望从该电路获得什么样的精度?
在本文中,我们将执行旨在回答三个问题的模拟。
- 理想条件下的输出电流有多精确?
- 负载变化如何影响输出电流的精度?
- 当考虑电阻容差时,典型和最坏情况下的精度是多少?
基线精度
这是我们将用于第一次模拟的电路:

施加到差分输入级的电压在 100 ms 间隔内从 –250 mV 变为 250 mV。输入电压与输出电流相关的公式告诉我们,流过负载的电流应为 V IN /100。
为了查看生成的负载电流与理论预测的匹配程度,我们将绘制模拟负载电流与数学计算负载电流之间的差异。
误差极小,其大小与负载电流的大小成正比。
负载调节
当我们谈论电压调节器时,负载调节是指调节器在负载电阻变化的情况下保持恒定电压的能力。我们可以将相同的概念应用于电流源:对于不同的 R LOAD值,电路如何保持指定的输出电流?
对于此仿真,我们将提供 250 mV 的固定输入电压,并且我们将使用“阶跃”指令以 10 Ω 的阶跃从 1 Ω 到 1000 Ω 改变负载。
“测量”指令允许我们绘制误差与步进参数(即负载电阻)的关系图,而不是与时间的关系图;这是通过打开错误日志(View -> SPICE Error Log),右击并选择“Plot .step'ed .meas data”来完成的。



对于更大的负载电阻,输出电流误差确实会显着增加——从大约 50 nA 增加到 800 nA。然而,800 nA 仍然是一个非常小的误差。
如果我们用旨在接近真实运算放大器性能的宏模型替换理想运算放大器,您认为负载调节会有多大变化?让我们来看看。


输出误差的变化百分比非常相似。在第一次模拟中,误差在负载电阻范围内增加了 15.7 倍。在第二个仿真中,我使用了 LT1001A 的宏模型,它增加了 12.1 倍。
有趣的是,LT1001A 的性能优于 LTspice“理想的单极点运算放大器”——误差幅度在整个范围内要低得多,而且误差相对于负载电阻更稳定。我不知道该如何解释。也许理想的单极运算放大器并不像我想象的那么理想。
电阻容差的影响
我们不需要模拟来确定 R1 电阻变化的影响;输入电压和输出电流之间的数学关系让我们清楚地了解偏离标称值的 R1 值会引入多少误差。
此外,应用笔记中的电路图显示了 R4 与 R2 的比率将如何影响输出电流,因为该比率决定了 A V,而 I OUT与 V IN乘以A V成正比。
然而,不太清楚的是电阻器之间不完美匹配的影响。电路图表明R2和R3要匹配,R4和R5要匹配。我们可以通过执行蒙特卡罗模拟来研究这一点,其中电阻值在其公差范围内变化。
如果仿真包括大量蒙特卡罗运行,则仿真结果中报告的最大和最小误差可以解释为与电阻容差相关的最坏情况误差。
对于此仿真,我们将 R2 和 R4 固定为 100 kΩ;这防止了 A V的变化。我们将通过对 R3 和 R5 的值应用蒙特卡罗函数来降低电路的匹配。

如“step”SPICE 指令所示,一次仿真包含 100 次运行。“mc(100k,0.01)”值指定 100 kΩ 的标称电阻,容差为 1%。
这是 100 次运行的输出电流误差图。

平均误差为 15.6 µA,是预期 2.5 mA 输出电流的 0.6%,在最坏情况下,实际输出电流与预期电流的偏差约为 40 µA。
我会称之为非常好的精度。让我们看看当我们使用 0.1% 的公差而不是 1% 时情况如何改善。


现在平均误差为 1.6 µA,仅为预期输出电流的 0.06%,最坏情况下的误差已降至 4 µA 范围。
结论
我们进行了 LTspice 仿真,为双运算放大器电流泵的性能提供了宝贵的见解。
1% 的电阻容差,确定输入增益的电阻器固定在其理论值,可实现高精度。将 0.1% 的容差应用于所有电阻器会提供良好的性能,并且由于 0.1% 的电阻器很容易买到而且不贵,我同意应用笔记作者推荐 0.1% 容差而不是 1% 容差的观点。
-
电路
+关注
关注
173文章
6018浏览量
174212 -
电流
+关注
关注
40文章
7095浏览量
133847 -
拓扑
+关注
关注
4文章
346浏览量
29891 -
LTspice
+关注
关注
1文章
123浏览量
13792
发布评论请先 登录
怎样识别精密电阻
什么是精密电阻器及相关应用
精密电流分流器的用途
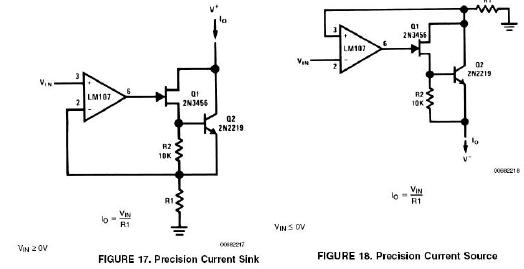
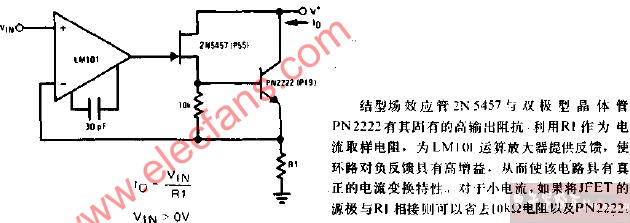
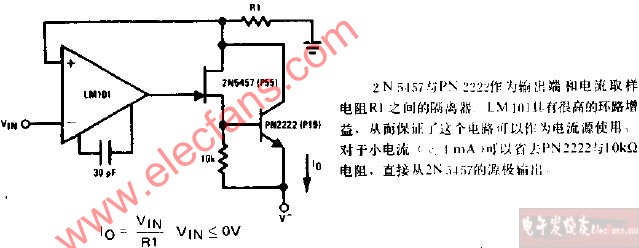
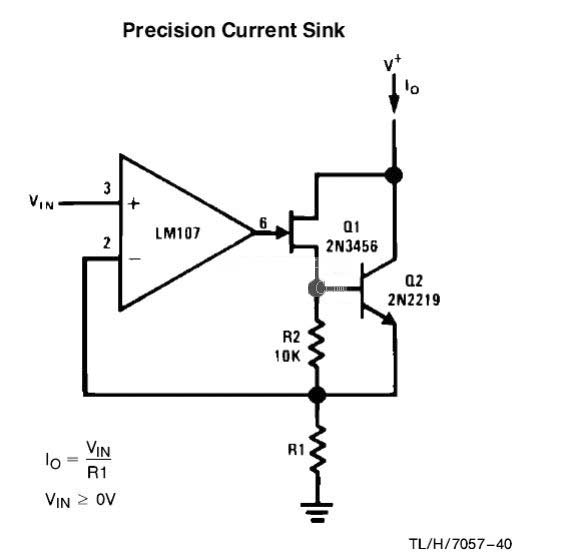
精密电流源:Precision Current Source





 剖析精密电流泵的LTspice性能
剖析精密电流泵的LTspice性能












评论