常用四轴的两种PID算法
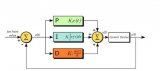
这里主要讲解的PID算法属于一种线性控制器,这种控制器被广泛应用于四轴上。要控制四轴,显而易见的是控制它的角度,那么最简单,同时也是最容易想到的一种控制策略就是角度单环PID控制器,系统框图如图所示:
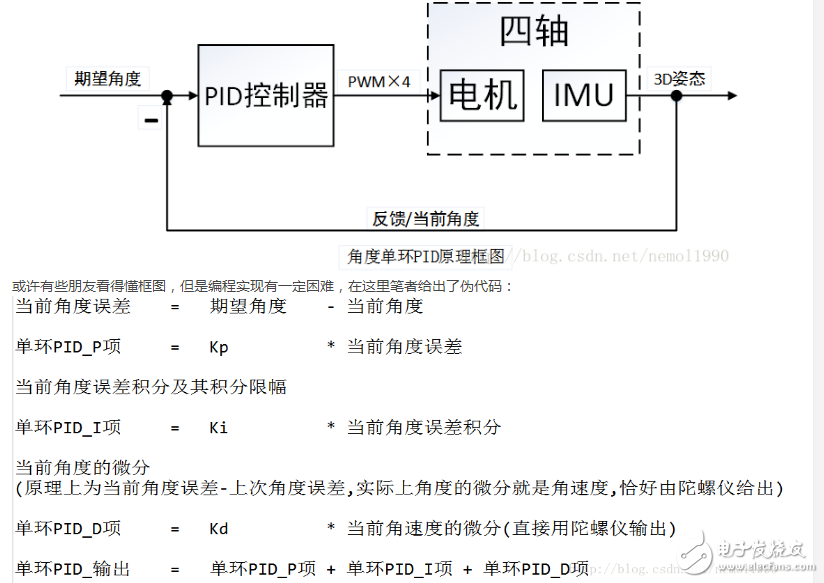
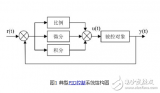
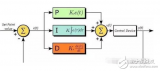
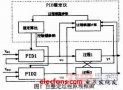
上述角度单环PID控制算法仅仅考虑了飞行器的角度信息,如果想增加飞行器的稳定性(增加阻尼)并提高它的控制品质,我们可以进一步的控制它的角速度,于是角度/角速度-串级PID控制算法应运而生。在这里,相信大多数朋友已经初步了解了角度单环PID的原理,但是依旧无法理解串级PID究竟有什么不同。其实很简单:它就是两个PID控制算法,只不过把他们串起来了(更精确的说是套起来)。那这么做有什么用?答案是,它增强了系统的抗干扰性(也就是增强稳定性),因为有两个控制器控制飞行器,它会比单个控制器控制更多的变量,使得飞行器的适应能力更强。为了更为清晰的讲解串级PID,这里笔者依旧画出串级PID的原理框图,如图所示:

同样,为了帮助一些朋友编程实现,给出串级PID伪代码:

四轴专用PID参数整定方法及原理
使用PID的四轴会在飞行中震荡,告诉大家为什么光使用PID并不能实现对四轴姿态‘足够好’的控制。文章中还是涉及了不少自控原理和其他控制相关的姿势,没有一点底子的话确实会看着很困惑(不然那么些人花好几年学控制还有什么意义?)。如果你只想知道结论的话,直接看文章开头和结尾部分就好了
PID控制器是什么?
我想每一个看到这里的人都对PID的概念有了足够的了解,我一遍遍叽歪比例积分微分没有任何意义。这里我只想说一些大家提的较少的‘重点’内容:
PID控制器是一个线性的控制器!从这里开始我们进入正题了,虽然若干年来PID已然成为了世界上使用最普遍的控制方法,也逐渐被人们神话到几乎可以控制一切………………但是,从理论上来说,只有‘线性的,符合要求的’被控系统才能在PID控制下实现良好的控制效果。
所以说,我们首先第一步,要保证我们的被控系统在被PID控制的区域‘表现为’一个线性系统才行。于是这里有人会说了,现实中没有哪个系统是线性的,自然,我们的四轴飞行器在大范围内是一个非常典型的非线性系统(随便按照理论推推模型就会出现漫天的三角函数),也就是说,我们‘仅’使用标准PID控制的话是不可能让四轴从各个姿态回到目标状态的过程都能保持稳定。于是这里出现我们使用PID时要注意的第一个问题:
我们的PID控制只能工作在四轴角度偏移不大的一个近似线性的区域内。这个区域没有定论,不过你要是飞机偏了90°的话想用PID调回到水平状态指定是非常危险的事情。PID的模型相关问题非常重要也比较费口舌,我们等下认真讨论,现在要先说另一个非常重要的非线性问题:
要保证我的控制通道与电机的输出力矩是线性的。如果我们的控制通道与电机输出力矩都不是线性的的话,我们的PID控制就很难起作用了,节省时间不举例子了,不明白的自行补脑吧,于是我这里要提醒大家的事情是:我们的航模电调调整的都是力矩而不是转速(虽然它叫做电子调速器),这是我们的福音,因为大家知道,螺旋桨产生的升力与转速的平方成正比,而角加速度与力矩成正比,正是因为我们的电调让电机产生的升力与我们输出的油门量成正比了我们才能使用PID控制器对四轴的姿态进行控制。这里可以看下我的四轴使用的四合一电调输出的升力与油门的对应曲线:

图中横坐标是输出油门的百分比,纵坐标是四个电机产生的总拉力(单位暂定kg),可以看到,具有非常好的线性关系,所以我们可以使用PID对大四轴实现比较好的控制。于是我们首先发现了第一个问题,有人反映小四轴不好调参数,因为小四轴没有专用的电子调速器,所以油门与输出力矩并不是严格线性的(这里我没有实践过,请大家随意批评指正),这时使用PID控制性能就会明显下降,当你的电机输出力矩与你的控制信号不是线性关系的时候,请先使用软件补偿的方法对油门做一下分段的线性仿射变化,再设计PID控制器。
不过对于大四轴而言貌似就不用那么麻烦了,那我们直接进入PID的控制模型环节。
PID控制器的数学模型
在标准的控制类书籍上PID算法是这么定义的:
这个公式是连续系统用的,我们单片机的控制是用不了的,我们的单片机使用的是离散的控制模型也叫0阶保持器的离散系统,就是需要把上面的公式离散化,而这个离散化的过程我们使用的是后项差分法。首先把上面的积分传递函数转化为连续的s域模型:
使用后向差分法可以得到s域到z域的映射关系:
于是可以得到:
这里特地给出了Kp Ki Kd这三个参数,这三个参数就是大家最常看到的那个离散的PID公式,也就是说你在这里既可以使用Kp Ti Td的参数来建模也可以使用Kp Ki Kd的参数来建模,到这里就总算是可以把我们的传递函数放在系统中用自控原理的相应工具来分析了。分析之前要先声明一个事情,有人发现(比如在MWC和其他许多飞控中)用陀螺仪的输出来当做PID中的微分项,会取得比标准PID更好的控制效果,乍一看这么做与用前后两次欧拉角作差没有区别(因为角速度整好就是角度的微分),控制效果不一样就说不通了。
其实是这个样子的,如果我们在程序中做了非常好的线程安全的处理并且控制频率和姿态解算读陀螺的频率是一样的的情况下二者确实是没有任何差别的,但是大家的飞控都写的非常简单,姿态解算频率都高于控制频率,于是读到的陀螺仪的数据并不是‘当前使用的姿态前一时刻’的数据而是‘后一时刻’的数据,这时候PID控制的微分部分就不再是‘后项差分’而是‘前向差分’了(这就是我前面要强调使用后项差分法的原因),那这个时候就尴尬了,我们不能全部使用前向差分模型来建模(因为积分还是使用的后向模型)两边分开用又会出现模型阶次不匹配的问题,所以这时候是无法使用PID模型来考虑接下来的问题的,你使用的其实是两个独立的控制器并联,一个是角度的PI控制器,而另一个是角速度的P控制器,二者采样时间不一样,于是得当做两个独立的控制回路调整参数,这是使用这种控制器时的参数调整方法。也就道出了为什么部分情况下使用角度微分和角速度控制效果不一样的问题,这种方法固然是很好的(可以有效的降低振动),当然前提是你按照二者独立控制的思路来设计参数。但是很不幸,大家都没有这么做,依然是把整体作为PID控制器来考虑,那么,我只能说这是个近似的PID控制器了,手调固然可以(万能的实验调参啊)但是通过建模的方式算出优化的参数就不可能了。我们接下来看会怎样:
从系统的零极点图理解PID控制的原理
有了上面的PID传递函数的离散系统模型我们就可以开始下一步了,将上面的分式上下做因式分解可以得到系统的零极点,在自控原理中我们知道,系统的极点确定系统的稳定性情况,零点不影响系统稳定性,零点和极点共同决定系统的响应。这里说的有些模糊,在现代控制理论中会提到一种控制器叫零极点配置控制器,能更好的阐述零点的作用:系统中的零点可以用来与系统中的不稳定(或者不想要)的极点对消来设计出理想的控制器(数学上),工程中我们考虑的是让零点与我们不想要的极点尽可能的靠近,就能削弱这个不想要的极点对系统的影响。下面我们用极点配置的方法来设计PID控制器,这里提前声明我们使用的并不是最标准的闭环极点配置方法,因为我们的PID控制器只有两个零点可以配置(如果使用PI控制器的话就只有一个零点可以自由配置了)而且还多了一个临界稳定的极点,反馈又使用的是单位负反馈……极大的限制了极点配置的自由度,于是我们为了简单起见仅从开环部分进行极点配置,这么做有许多不严谨的地方,但是会简化许多工程上的应用(在做自适应PID控制器的时候会用到完整的极点配置方法,到那里就会发现是多么复杂的一件事儿了……)。
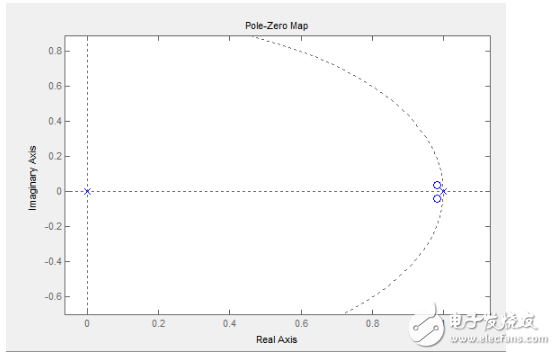
上图是PID控制器开环部分(就是上面推导的数学模型)常见的零极点分布情况,有两个固定在(0,0)和(1,0)位置的极点,两个对称分布的零点(手调参数时很难出现两个零点都在实轴上的情况而且我们也不希望那样),这两个零点的位置是可调的,微分时间常数Td主管零点位置的左右移(注意是‘主管’,也就是说对虚轴的位置还是有影响的),常数越大越靠右(也就是说临界稳定极点的影响越弱,抗噪声性能越好但到达0误差的稳态也就越困难,因为这个临界稳定的极点是在闭环系统中让系统到达稳态0误差的关键但很影响稳定性),积分常数Ti越大零点越靠近实轴,Ti在实际控制中的作用不好说明,留在后面再说,但是到这里大家也就看出我为什么要使用标准的Kp Ti Td参数而不是Kp Ki Kd参数了,因为使用这种参数时Kp对开环系统的稳定性(注意仅指开环系统)没有影响,我们就可以降低系统对这个参数的敏感性而主要考虑另外两个参数就好。大家在手调参数的看到的图形和这个都应该没有多少区别
接下来我们看一下我们被控系统的数学模型:
被控系统的小范围线性化模型
正如我前面所述,想要分析PID的控制性能必须得得到被控系统的线性近似模型(非线性系统下的分析工具没个正经能用的),这里大家可以通过动力学建模得到系统的非线性模型(像几乎所有的硕士博士论文那样)再泰勒展开,但是这样做往往得到的模型跟实际情况差异太大以至于没有参考价值,这里我推荐使用系统辨识的方法来得到系统的线性模型,因为这么做如果能做到正确的辨识的话还能得到系统的误差模型,于是现在在控制界很流行,只是实际用的时候就发现难度颇高,尽管有许多现成的工具但是依然特别难掌握,也难怪很多热会把这个当做是看家本领,作者在这方面也算是连皮毛都没摸全,不敢乱讲,这里就为了解释PID方便直接把我的大四轴辨识出来的Pitch轴模型拿出来当做例子来讲了:
画出来的系统阶跃响应是这个样子的:
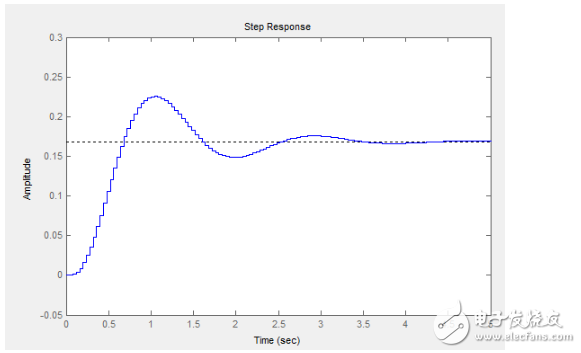
检验系统建模的相似程度就靠这个了,给我的飞机一个阶跃信号反映出来的情况和这个确实差不多。关键是下面,它的零极点分布情况:
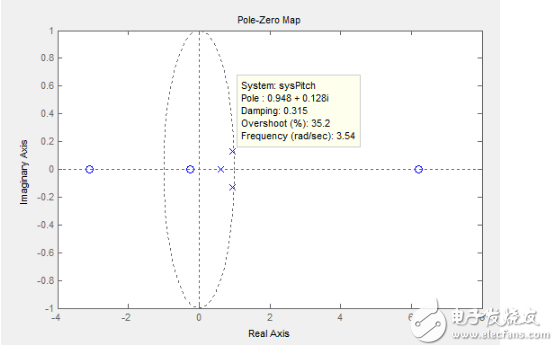
可以看到辨识出来的结果又两个很靠近不稳定边界的主导极点(气泡框那里)表现明显的零点又和这几个极点8杆子打不着,如果我们消灭那两个主导极点,我们的四轴理论上就可以控制的非常完美了,众所周知,主导极点越靠近0则系统稳定性越好,那么按照极点配置的方法(当然我这里指的还是开环的极点配置),那么我们接下来开始看用这种建模的方法怎么实现PID参数的配置:
用极点配置PID实现对系统的控制
那么按照上面的介绍我们来尝试消除这两个主导极点,前面说过,PID模型中两个对称零点的位置是可以任意调整的,不用计算,直接手试出如下的参数:
那么得到的开环零极点图是这样的:
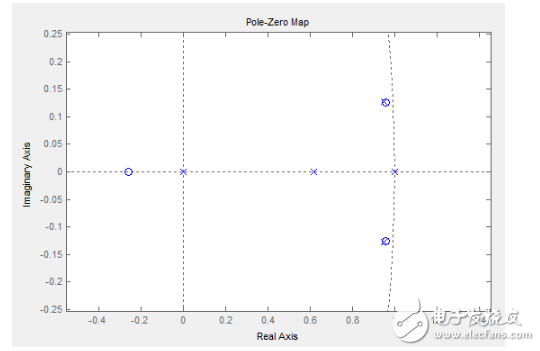
那么闭环响应是这个样子的:
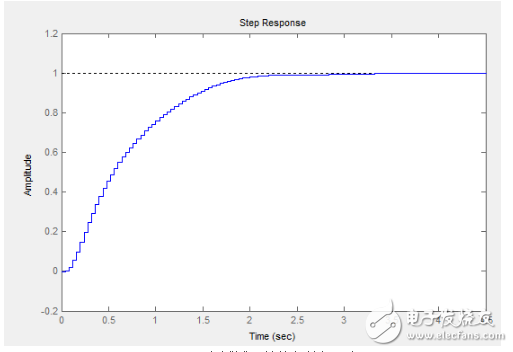
看着很漂亮啊,我们加大Kp到4试试,其他参数都不变

哟,完美嘛,0.5s即可到达稳态,0稳态误差,超调量也不过10%而已,相当的理想,而且从这里可以看出使用Kp Ti Td参数的优势:随意调整Kp,可以提高系统性能而且对闭环稳定性几乎没有影响,甚至对开环系统的稳定性完全没有影响,我想,这也就是MWC飞控用Kp(角速度的)作为动态参数的原因。那么好吧,令人沮丧的部分终于要来了,把这个参数烧到飞控里面,运行,哇塞,不错哦,不动摇杆它平衡的很好,那我们遥控下……我擦,越抖越大,控制不住了,翻了,打到人了,鲜血汩汩而出……………………
这是为什么呢?来看下我们这时的开环系统阶跃响应:
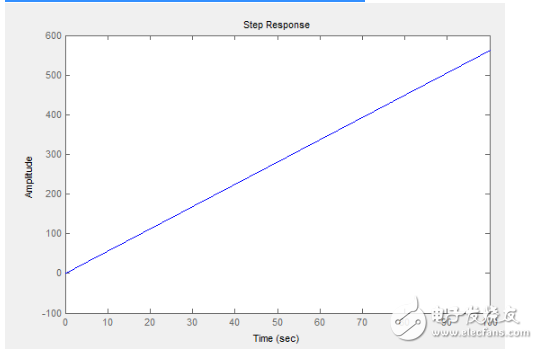
咦?怎么是一条直线呢?没错,它就是这样一个不稳定的状态,在我们高兴的做极点配置的时候,忘记了PID控制器本身还会引入一个临界稳定的极点,这个极点带来的好处0稳态误差,但是却对噪声非常敏感,也就是说,如果我们的飞机在气流平稳的地方飞行,飞机的电机性能又极佳,建模也准,最关键的,是姿态解算的精度又出奇的高的话,用这种方法得到的PID参数肯定是非常完美的。但是现实总是残酷的,具体为什么会对噪声这么敏感应该可以从系统的噪声辨识模型中得到解释,但是很遗憾到文章这里我并没有对噪声进行建模,有兴趣的可以尝试下。
这里就是使用PID控制的弊端了,它只提供了两个零点用来对极点进行抑制,但是又同时引入了一个不稳定的极点,不得已,我们只能让零点从那两个极点上向那个临界稳定的极点移动,企图用两个零点来牵制三个极点,这自然没办法达到良好的控制效果,但也就成了没有办法的办法了……大家在搜索PID参数整定方法的时候一定都听说过Ziegler-Nichols整定法则,这几乎是PID基于模型的参数整定唯一的方法了,但是为什么没人把这个如此著名的整定方法(这里指第一方法)应用在四轴的PID整定中呢?因为使用该法则有个铁打的前提:控制对象中既不能包含积分器,又不包含主导共轭复数极点,也就是说阶跃响应应该是一个S型…………………………很不幸,我们的四轴这两条都占了……积分器是在从角速度到角度转换的过程中,在与其他好多极点的共同作用中最终在我们的参数辨识中表现为了那两个讨厌的共轭复数极点,重新看一遍我的解释流程,就明白为什么不能用Ziegler-Nichols整定第一法则了,也就是为什么光用PID不能达到足够好的控制效果。
那么,既然非要用PID飞又既然缺少极点的情况下我们只能让零点右移,这么做的理由也是可以从另一个方面来佐证的:
调过PID的都知道增加微分可以提高系统的抗噪性能,减小积分会减小噪声积累(这里指Ki增加而不是Ti)反映到零点的移动中刚好就是零点向右侧的(1,0)点移动。所以可以得知,我们经过权衡能得到的PID最佳的控制参数的零点应该是落在了开环主导极点和(1,0)点连线所在的那一片区域内了,那么我们对PID的分析是否到此就结束了呢?显然没有,我还没有论证为什么大家在数年的总结中会得到“先调P,再调D,最后调I就能飞了”的实验整定方法能够凑效,并且还要提出个理论指导实践的方法来……
自控原理的书上有提到“串联响应频率校正”的设计方法,但是该方法屡试都不爽,有兴趣可以从这个方向走走,说不定能为我们的四轴PID控制器设计找到一条出路。
之前我曾说过,用Kp Ti Td型的参数设计的PID控制器稳定性对Kp并不敏感,那么我们是不是可以利用这点来优化我们的控制器设计呢?答案是肯定的。我们先来看下按照上面的‘向右看齐’参数调整方法会发生什么:
我们随便选一个在连线上的点作为参数查看它的开环零极点和闭环阶跃响应(这里Kp去1):
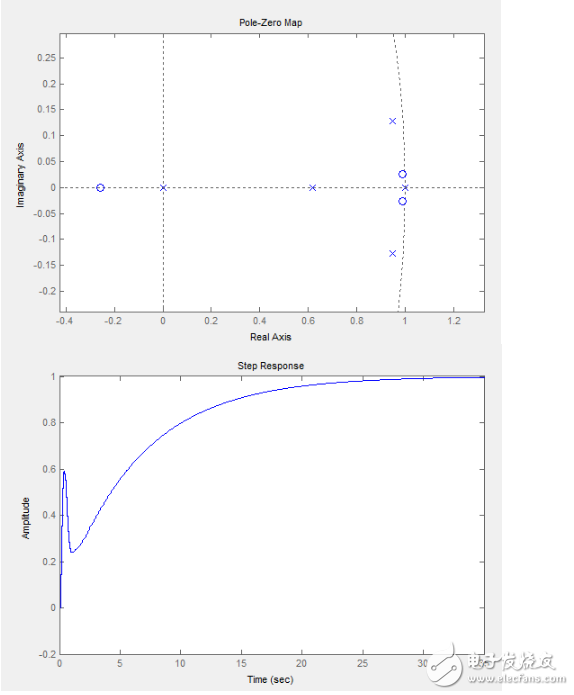
可以看到,积分的效果明显减弱了,系统先在0.几秒的时候迅速的达到了稳态(0.3左右)然后在以后漫长的时间内在积分作用的影响下以指数逼近最终的稳态1,大家看着这个图应该很快就想到该怎么做了,就是增大Kp,让系统的‘第一个’稳态在1附件,那问题就解决了,不错,我们这里把Kp设为4(不设置为3是为了等下验证另一个东西):
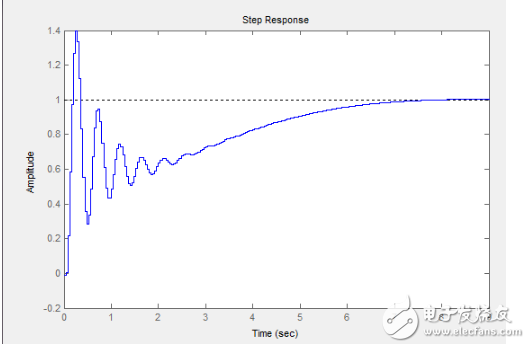
瞧,这个很丑的怪物出现了,比刚才好了不少,而且你最终得到的PID控制器输出效果会和这个差不了许多(之所以在视频上看不出来是因为人很少会从0----Pitch角0°突然给飞机一个1----Pitch角57°)另外要说的是为什么我用了4依然没有让它的第一步就稳定到1,这是因为闭环降低了系统总增益,但是这里给再高的增益会让系统不稳定,原因就在下面了:
为了更直观的说明不稳定的原因,这里要用Bode图来看一下系统闭环的频域响应:
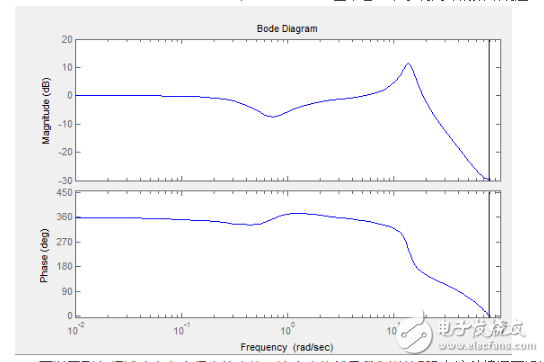
可以看到在频域响应有个很尖的尖峰,这个尖峰就是我们说的PID在这种情况下没法达到优良控制性能的关键,你会发现,使用纯PID控制的飞控,都会在空中来回抖动,频率基本是固定的,就是这个尖峰的缘故,尤其当Pitch轴和Roll轴使用同样的控制参数的时候,抖动会叠加,你经常会看到视频里用纯PID控制的四轴在两个控制轴交界的方向上抖啊抖抖啊抖抖啊抖抖啊抖…………于是这里就是我们需要用实验来权衡的地方,这个尖峰通过减小Kp的值可以得到一定的抑制,也可以让零点向左少许移动,二者都会延长到达稳态的时间,比较明智的做法是保证有足够的响应速度的前提下适当减小增益,毕竟在PID没法很好的完成控制任务的情况下,人的操作就显得非常重要了。这里给出我使用的一组PID参数:
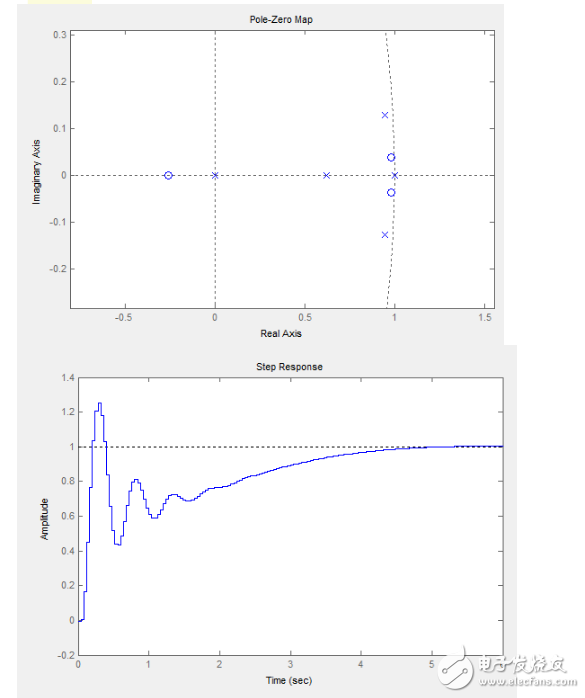
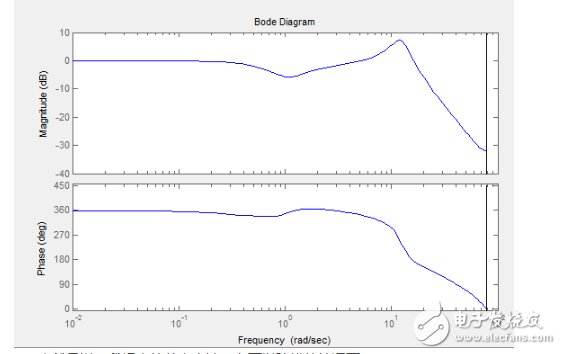
也就是说,我提出的整定方法,在可以建模的情况下:
①建立被控系统的模型
②根据上述的原则确定PID的开环0点应该出现的区域(就是在那个连线上)
③给一个开环情况下稳态误差较小的Kp
④看着阶跃响应微调Ti和Td使得在保证Td足够大的情况下超调量较小且积分效果打到稳态的时间又足够的长(2~3s以上依据个人口味)
⑤最后看着Bode图适当减小增益Kp
⑥回头再检查下阶跃响应是否满足心意就完事儿了
看到这儿,不知道有多少人会和我一样苦苦的一笑(这TM繁琐的步骤有意思吗?),这么做确实是一件非常不值得的事情,只是如我这般不服气的孩子凭着一股刨根问底的冲劲花了2个月用自己的方式来调PID的真实记录而已,好了,现在再来介绍不建模的情况下怎么通过试验整定四轴的PID参数
其实试验方法整定PID参数使用的依然是Ziegler-Nichols整定法则,不过这次使用的是第二法则,而且做完以后要按照我接下来给的步骤微调
鉴于该整定法则在阿莫上没有人提过(至少我没有找到),这里先贴上完整的Ziegler-Nichols整定第二法则:
首先,该法则使用Ti Td的参数形式(现在更理解为什么要用Ti Td参数格式了吧?)先仅使用Kp进行控制(取Ti为无穷大,比如32767,取Td为0,等价于Ki=0 Kd=0)从0开始慢慢增大Kp直到第一次出现临界稳定的情况记录下当前的Kp值计作Kc……
这里暂停一下,注意这里的临界稳定的含义,调参时请用一根圆杆子横穿四轴的重心,这个时候四轴会在杆子上等幅摆动,这个时候可不是临界稳定啊!四轴风扇油门推到很大的时候气流是会给一定旋转的阻力的,如果你Kp调到没过5它就等幅震荡了那绝对是不对的,要把油门推到飞机平时刚好起飞的位置(既杆子与飞机接触面基本不受力)。另外就是等幅震荡并不是说你把它放在那儿它慢慢岳震越大了,而是你给个阶跃响应它按照那个幅度等幅震荡,比如你用手轻轻拨了一下,它就在那个范围等幅震荡了。这个点很精确,多一小点就发散,少一小点就能慢慢停下来,比如我的四轴测完是11.6
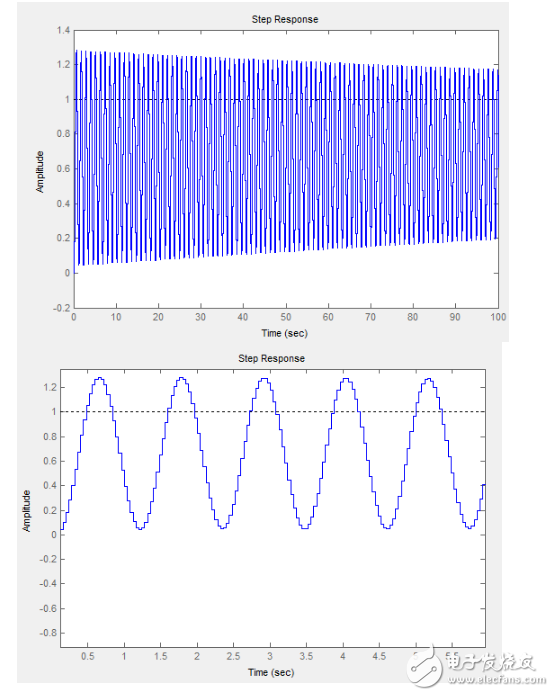
…………继续,则这时你需要测量它震荡一个周期的时间(单位为s)计做Pc,那我们就可以得到用Ziegler-Nichols整定第二法则得到的PID参数:
Kp = 0.6Kc
Ti = 0.5Pc
Td = 0.125Pc
我们看下这个参数的阶跃响应和开环零极点:
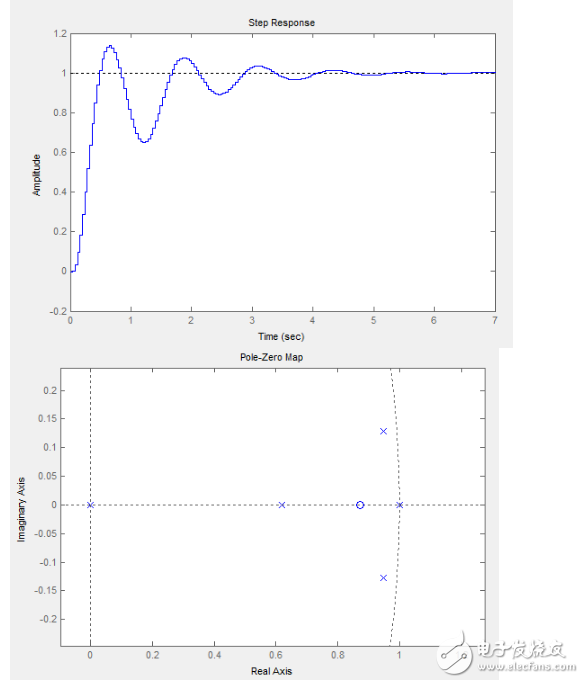
你会发现它只有一个零点,其实这并不是一个零点,而是两个零点重合了,但是你把这个参数烧到四轴上以后出现的情况和我前面的极点配置方法得到的情况非常相像,因为它的微分系数太小了,抵抗扰动的能力很弱,这里要说明为什么他要用一个重合的零点,大家在做控制的时候很少遇到这种震荡特性很强的系统,大家遇到的基本都是一阶的系统(阶跃函数表现为单调增到达稳态),这时候用这种无虚部的零点可以让超调量最小。
那么,也许有很多人跟我一样,刚开始调PID的时候两次调到这里,一次是应为震荡点没选对,Kc小了太多导致控制完全不起作用于是放弃了。第二次调对了Kc但是发现稳态效果很差,在Ki Kd的参数下折腾了好久越调越烂最终把这个方法放弃了。我估计到现在坛子里没见到这个整定方法很有可能就是这个原因吧。
那么好了,我这里要告诉你到了这一步该怎么继续调,不要动Kp和Ti,增大Td直到你觉得快速用手转动你的四轴的时候有了足够的阻力(注意是快速转动的过程中,而不是你压着它不动的时候的阻力),这时候你的四轴应该就已经调好了,想进一步微调就是你自己的事情了,让我们来看下这个时候系统是什么样子的,我们仅给这时的Td参数加上0.5(取个比较整的数而已,要是取1就更明显了)
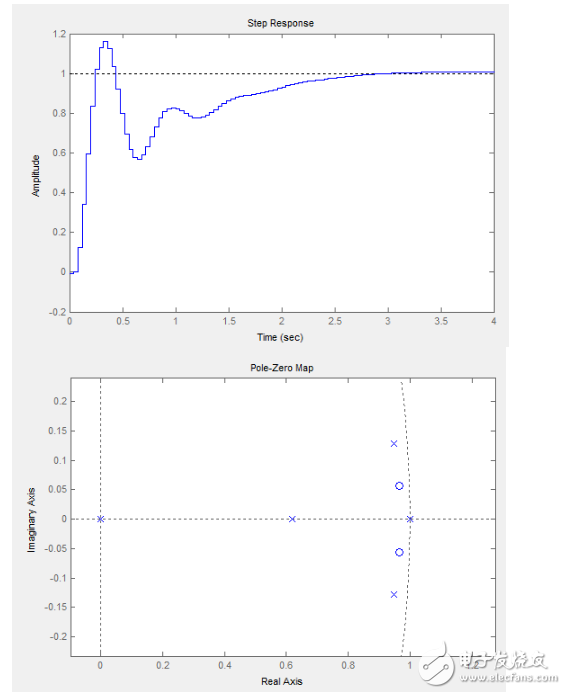
有没有发现和我前面得到的参数非常接近?看着这个图,结合前面我提到的内容,又有什么感悟呢?
维基百科上有个词条《齐格勒-尼科尔斯方法》,里面用的是Ki Kd的参数形式,需要用我前面提到的Ki Kd和Ti Td的转换关系转换一下。
总结:PID该怎么调,我们该注意什么
①先要保证电机的输出是线性的,微型四轴等没有电调的最好先对电机的油门行程和供电电压进行矫正,保证对电机的控制输入和电机输出的力矩程线性关系。
②严格注意自己控制程序中的每一步是否有线程安全的问题,不要让四轴的一次控制运算中使用了不是同一时间的状态测量值。
③用陀螺作为微分项能减少姿态解算误差带来的干扰,但要小心有可能会破坏了PID的控制模型导致控制效果变坏。
④作者强烈建议你使用Kp Ti Td的PID参数形式。
⑤记住Kp Ti Td参数变化对系统产生的影响是什么样的。
⑥注意调参的时候你是怎么固定你的四轴的。
⑦选择我上面提到的我的两种调参方法的一种整定参数。
⑧不要相信仅用PID能调出完美的四轴控制器,PID仅仅能让你的四轴飞起来而已,更不要相信增量式PID能在四轴的姿态控制中有所作为,牛逼的开源不开源四轴都不仅仅使用了PID控制器。
⑨不要手贱报控制专业
这里附上MATLAB的仿真代码
[plain] view plain copy%% lynx的四轴飞行器PID调试模型
clc,clear
%被控线性模型
TfPitchNum = [-0.00004584 0.0001312 0.0009171 0.000228];
TfPitchDen = [1 -2.514 2.087 -0.5657];
sysPitch = tf(TfPitchNum,TfPitchDen,0.04); %重新构造无噪声输入的模型
%ltiview(sysPitch)
sysPitchZpk = zpk(sysPitch);
%使用标准PID参数的柿子,这个是一个可用的参数
Kp = 6.5;
Ti = 0.8;
Td = 1.1;
% %临界稳定增益
% Kp = 11.6;
% Ti = 1000;
% Td = 0;
% %齐格勒-尼克尔思整定方法
% Kp = 11.6*0.6;
% Ti = 0.5*1.1;
% Td = 0.125*1.1+0.5;
Ts = 0.04
Ki = Kp*Ts/Ti; %0.3
Kd = Kp*Td/Ts; %17
p2 = Kd;
p1 = -Kp-2*p2;
p0 = Kp+Ki+p2;
ControlSys1Num = [p0 p1 p2];
ControlSys1Den = [1 -1 0];
ControlSys1 = tf(ControlSys1Num,ControlSys1Den,0.04);
SysOpen = series(ControlSys1,sysPitchZpk);
SysSum = feedback(SysOpen,1)
ltiview(SysSum)
ltiview(SysOpen)
%ltiview(ControlSys1)
tf(ControlSys1)
 电子发烧友App
电子发烧友App




















评论