KMeans算法是最常用的聚类算法,主要思想是:在给定K值和K个初始类簇中心点的情况下,把每个点(亦即数据记录)分到离其最近的类簇中心点所代表的类簇中,所有点分配完毕之后,根据一个类簇内的所有点重新计算该类簇的中心点(取平均值),然后再迭代的进行分配点和更新类簇中心点的步骤,直至类簇中心点的变化很小,或者达到指定的迭代次数。
KMeans算法本身思想比较简单,但是合理的确定K值和K个初始类簇中心点对于聚类效果的好坏有很大的影响。
1. 确定K个初始类簇中心点
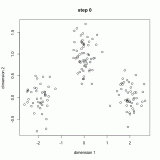
最简单的确定初始类簇中心点的方法是随机选择K个点作为初始的类簇中心点,但是该方法在有些情况下的效果较差,如下(下图中的数据是用五个二元正态高斯分布生成的,颜色代表聚类效果):

《大数据》一书中提到K个初始类簇点的选取还有两种方法:
1)选择彼此距离尽可能远的K个点
2)先对数据用层次聚类算法或者Canopy算法进行聚类,得到K个簇之后,从每个类簇中选择一个点,该点可以是该类簇的中心点,或者是距离类簇中心点最近的那个点。
1) 选择批次距离尽可能远的K个点
首先随机选择一个点作为第一个初始类簇中心点,然后选择距离该点最远的那个点作为第二个初始类簇中心点,然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点,以此类推,直至选出K个初始类簇中心点。
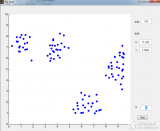
该方法经过我测试效果很好,用该方法确定初始类簇点之后运行KMeans得到的结果全部都能完美区分五个类簇:

2) 选用层次聚类或者Canopy算法进行初始聚类,然后利用这些类簇的中心点作为KMeans算法初始类簇中心点。
常用的层次聚类算法有BIRCH和ROCK,在此不作介绍,下面简单介绍一下Canopy算法,主要摘自Mahout的Wiki:
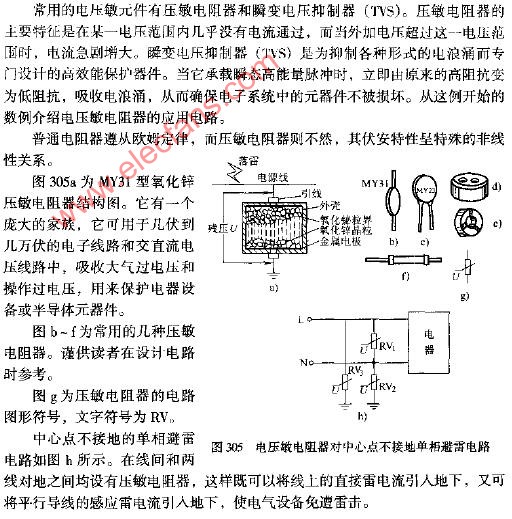
首先定义两个距离T1和T2,T1》T2.从初始的点的集合S中随机移除一个点P,然后对于还在S中的每个点I,计算该点I与点P的距离,如果距离小于T1,则将点I加入到点P所代表的Canopy中,如果距离小于T2,则将点I从集合S中移除,并将点I加入到点P所代表的Canopy中。迭代完一次之后,重新从集合S中随机选择一个点作为新的点P,然后重复执行以上步骤。
Canopy算法执行完毕后会得到很多Canopy,可以认为每个Canopy都是一个Cluster,与KMeans等硬划分算法不同,Canopy的聚类结果中每个点有可能属于多个Canopy。我们可以选择距离每个Canopy的中心点最近的那个数据点,或者直接选择每个Canopy的中心点作为KMeans的初始K个类簇中心点。
K值的确定。
《大数据》中提到:给定一个合适的类簇指标,比如平均半径或直径,只要我们假设的类簇的数目等于或者高于真实的类簇的数目时,该指标上升会很缓慢,而一旦试图得到少于真实数目的类簇时,该指标会急剧上升。
类簇的直径是指类簇内任意两点之间的最大距离。
类簇的半径是指类簇内所有点到类簇中心距离的最大值。
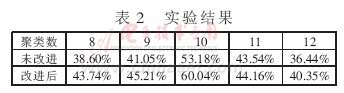
废话少说,上图。下图是当K的取值从2到9时,聚类效果和类簇指标的效果图:


左图是K取值从2到7时的聚类效果,右图是K取值从2到9时的类簇指标的变化曲线,此处我选择类簇指标是K个类簇的平均质心距离的加权平均值。从上图中可以明显看到,当K取值5时,类簇指标的下降趋势最快,所以K的正确取值应该是5.为以下是具体数据:
《span style=“background-color: white;”》2 个聚类
所有类簇的半径的加权平均值 8.51916676443
所有类簇的平均质心距离的加权平均值 4.82716260322
3 个聚类
所有类簇的半径的加权平均值 7.58444829472
所有类簇的平均质心距离的加权平均值 3.37661824845
4 个聚类
所有类簇的半径的加权平均值 5.65489660064
所有类簇的平均质心距离的加权平均值 2.22135360453
5 个聚类
所有类簇的半径的加权平均值 3.67478798553
所有类簇的平均质心距离的加权平均值 1.25657641195
6 个聚类
所有类簇的半径的加权平均值 3.44686996398
所有类簇的平均质心距离的加权平均值 1.20944264145
7 个聚类
所有类簇的半径的加权平均值 3.3036641135
所有类簇的平均质心距离的加权平均值 1.16653919186
8 个聚类
所有类簇的半径的加权平均值 3.30268530308
所有类簇的平均质心距离的加权平均值 1.11361639906
9 个聚类
所有类簇的半径的加权平均值 3.17924400582
所有类簇的平均质心距离的加权平均值 1.07431888569《/span》
uk是第k 个类的重心位置。成本函数是各个类畸变程度(distortions)之和。每个类的畸变程度等于该类重心与其内部成员位置距离的平方和。若类内部的成员彼此间越紧凑则类的畸变程度越小,反之,若类内部的成员彼此间越分散则类的畸变程度越大。求解成本函数最小化的参数就是一个重复配置每个类包含的观测值,并不断移动类重心的过程。
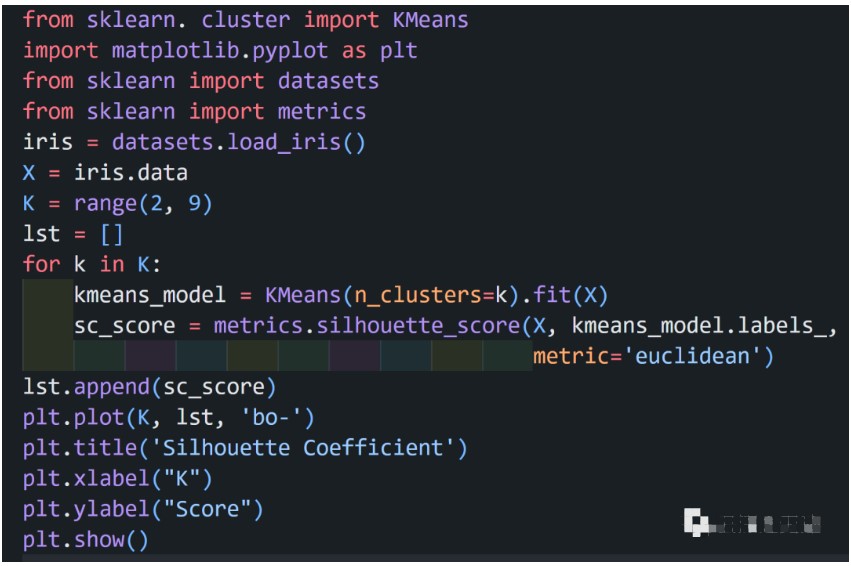
#-*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import sys
reload(sys)
sys.setdefaultencoding(‘utf-8’)
x = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
y = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
data = np.array(list(zip(x, y)))
# 肘部法则 求解最佳分类数
# K-Means参数的最优解也是以成本函数最小化为目标
# 成本函数是各个类畸变程度(distortions)之和。每个类的畸变程度等于该类重心与其内部成员位置距离的平方和
‘’‘’‘aa=[]
K = range(1, 10)
for k in range(1,10):
kmeans=KMeans(n_clusters=k)
kmeans.fit(data)
aa.append(sum(np.min(cdist(data, kmeans.cluster_centers_, ’euclidean‘),axis=1))/data.shape[0])
plt.figure()
plt.plot(np.array(K), aa, ’bx-‘)
plt.show()’‘’
#绘制散点图及聚类结果中心点
plt.figure()
plt.axis([0, 10, 0, 10])
plt.grid(True)
plt.plot(x,y,‘k.’)
kmeans=KMeans(n_clusters=3)
kmeans.fit(data)
plt.plot(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],‘r.’)
plt.show()
 电子发烧友App
电子发烧友App









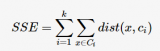


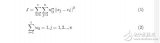










评论