2、反向投影直方图检测ROI
图像直方图是什么?其实就是与图像某一特征有关的数据集合的统计关系,反应在归一化直方图中则是与该图像特征有关的数据集合的概率关系。图像某一子区域的直方图可以看做是一个概率函数,它给出的是某个像素属于该区域纹理特征的概率。还是上例子吧。

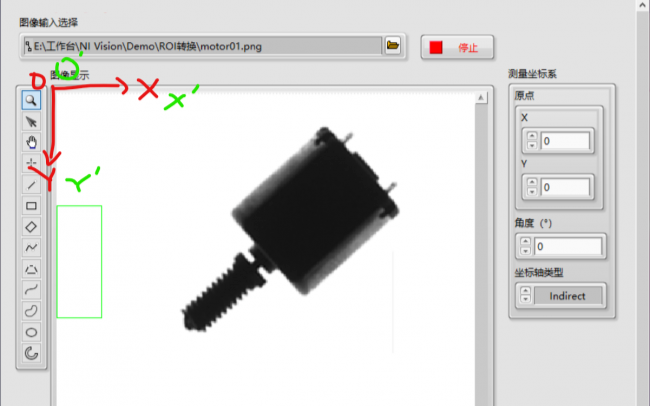
1) 求出上面灰度图中矩形框标记出的区域的归一化灰度直方图,为方便理解直方图的每个bin只有一个像素,则每个bin的数值不就是这一像素值在图片中出现的概率么。
2) 遍历上面图像中的每个像素,获取其灰度值在直方图(矩形框标记区域)的bin的数值,用该数概率值代替原来像素的灰度值。
3) 得到的概率映射图的每一像素不就代表了它属于标记区域的概率么?
从上例我们可以抽象出,方向投影直方图的作用是在于替换一个输入图像中每个像素值,使其变成归一化直方图中对应的概率值。OpenCV提供了反向投影直方图操作的API函数calcBackProject,其函数原型为:
void calcBackProject(const Mat* arrays, //原始图像
int narrays, //原始图像张数
const int* channels, //原始图像通道数量
const SparseMat& hist, //进行反投影的直方图
OutputArray backProject,//生成的反向投影图像
const float** ranges, //直方图每个维度的值域
double scale=1, //缩放因子
bool uniform=true ) //是否均匀12345678
很多参数与calcHist的意义类似,缩放因子表示对得到的反向投影图像的每个“像素”可乘以一浮点数进行缩放。
程序如下:
//CalcHistogram.h
#pragma once
#include “opencv2/core/core.hpp”
#include “opencv2/imgproc/imgproc.hpp”
#include “opencv2/highgui/highgui.hpp”
using namespace cv;
class CalcHistogram
{
private:
int histSize[3]; //直方图项的数量
float hranges[2]; //h通道像素的最小和最大值
float sranges[2];
float vranges[2];
const float *ranges[3]; //各通道的范围
int channels[3]; //三个通道
int dims;
Mat histogram; //用来存放 待反投影 的归一化直方图
public:
CalcHistogram(int hbins=90, int sbins=128, int vbins=128);
~CalcHistogram(void);
//计算直方图
Mat getHistogram(const Mat &image);
//画出直方图
void getHistogramImage(const Mat &image);
//直方图归一化
void setHistogram(const Mat& h);
//反投影直方图检测ROI
Mat reverseHistogram(const Mat& image);
};
12345678910111213141516171819202122232425262728293031323334353637
CalcHistogram.cpp
//CalcHistogram.cpp
#include “CalcHistogram.h”
CalcHistogram::CalcHistogram(int hbins, int sbins, int vbins)
{
histSize[0]=hbins;
histSize[1]=sbins;
histSize[2]=vbins;
hranges[0]=0; hranges[1]=180;
sranges[0]=0; sranges[1]=256;
vranges[0]=0; vranges[1]=256;
ranges[0]=hranges;
ranges[1]=sranges;
ranges[2]=vranges;
channels[0]=0;
channels[1]=1;
channels[2]=2;
dims=3;
}
CalcHistogram::~CalcHistogram(void)
{
}
Mat CalcHistogram::getHistogram(const Mat &image)
{
Mat hist;
calcHist(&image,
1,
channels,
Mat(),
hist,
dims,
histSize,
ranges,
true, //直方图是均匀的
false
);
return hist;
}
void CalcHistogram::getHistogramImage(const Mat &image)
{
Mat hist=getHistogram(image);
int scale = 4;
int hbins=histSize[0];
int sbins=histSize[1];
int vbins=histSize[2];
float *hist_sta = new float[sbins];
float *hist_val = new float[vbins];
float *hist_hue = new float[hbins];
memset(hist_val, 0, vbins*sizeof(float));
memset(hist_sta, 0, sbins*sizeof(float));
memset(hist_hue, 0, hbins*sizeof(float));
for( int s = 0; s 《 sbins; s++ )
{
for( int v = 0; v 《 vbins; v++ )
{
for(int h=0; h《hbins; h++)
{
float binVal = hist.at《float》(h, s, v);
hist_hue[h] += binVal;
hist_val[v] += binVal;
hist_sta[s] += binVal;
}
}
}
double max_sta=0, max_val=0,max_hue=0;
for(int i=0; i《sbins; ++i)
{
if(hist_sta[i]》max_sta)
max_sta = hist_sta[i];
}
for(int i=0; i《vbins; ++i)
{
if(hist_val[i]》max_val)
max_val = hist_val[i];
}
for(int i=0; i《hbins; ++i)
{
if(hist_hue[i]》max_hue)
max_hue = hist_hue[i];
}
Mat sta_img = Mat::zeros(240, sbins*scale+20, CV_8UC3);
Mat val_img = Mat::zeros(240, vbins*scale+20, CV_8UC3);
Mat hue_img = Mat::zeros(240, hbins*scale+20, CV_8UC3);
for(int i=0; i《sbins; ++i)
{
int intensity = cvRound(hist_sta[i]*(sta_img.rows-10)/max_sta);
rectangle(sta_img, Point(i*scale+10, sta_img.rows-intensity),Point((i+1)*scale-1+10, sta_img.rows-1), Scalar(0,255,0), 1);
}
for(int i=0; i《vbins; ++i)
{
int intensity = cvRound(hist_val[i]*(val_img.rows-10)/max_val);
rectangle(val_img, Point(i*scale+10, val_img.rows-intensity),Point((i+1)*scale-1+10, val_img.rows-1), Scalar(0,0,255), 1);
}
for(int i=0; i《hbins; ++i)
{
int intensity = cvRound(hist_hue[i]*(hue_img.rows-10)/max_hue);
rectangle(hue_img, Point(i*scale+10, hue_img.rows-intensity),Point((i+1)*scale-1+10, hue_img.rows-1), Scalar(255,0,0), 1);
}
imshow(“Shist”, sta_img);
imshow(“Vhist”, val_img);
imshow(“Hhist”, hue_img);
delete[] hist_sta;
delete[] hist_val;
delete[] hist_hue;
}
void CalcHistogram::setHistogram(const Mat& h)
{
histogram = h;
normalize(histogram,histogram, 1.0);
}
Mat CalcHistogram::reverseHistogram(const Mat& image)
{
Mat mapImg; //反向投影直方图之后得到的概率图
calcBackProject(&image,
1,
channels,
histogram,
mapImg,
ranges,
255.0
);
return mapImg;
}
//main.cpp
#include 《iostream》
#include “CalcHistogram.h”
using namespace std;
bool draw;
Mat src;//原始图像
Mat hsv;//原图转化为hsv
Mat roi;//ROI图像
Point cursor;//初始坐标
Rect rect;//标记ROI的矩形框
void onMouse(int event, int x, int y, int flags, void *param)
{
Mat img = hsv.clone();
switch (event)
{
//按下鼠标左键
case CV_EVENT_LBUTTONDOWN:
//点击鼠标图像时,清除之前ROI图像的显示窗口
cvDestroyWindow(“ROI”);
//存放起始坐标
cursor = Point(x, y);
//初始化起始矩形框
rect = Rect(x, y, 0, 0);
draw = true;
break;
//松开鼠标左键
case CV_EVENT_LBUTTONUP:
if (rect.height 》 0 && rect.width 》 0)
{
//将img中的矩形区域复制给roi,并显示在SignROI窗口
roi = img(Rect(rect.x, rect.y, rect.width, rect.height));
rectangle(img, rect, Scalar(0, 0, 255),2);
namedWindow(“SignROI”);
imshow(“SignROI”, img);
//将画过矩形框的图像用原图像还原
hsv.copyTo(img);
imshow(“SrcImage”, img);
//显示ROI图像
namedWindow(“ROI”);
imshow(“ROI”, roi);
//计算ROI的直方图并归一化
CalcHistogram h;
Mat hist=h.getHistogram(roi);
h.setHistogram(hist);
//在hsv图像上反向投影ROI的归一化直方图
Mat mapImage=h.reverseHistogram(hsv);
imshow(“mapImage”, mapImage);
waitKey(0);
}
draw = false;
break;
//移动光标
case CV_EVENT_MOUSEMOVE:
if (draw)
{
//用MIN得到左上点作为矩形框的起始坐标,如果不加这个,画矩形时只能向一个方向进行
rect.x = MIN(x, cursor.x);
rect.y = MIN(y, cursor.y);
rect.width = abs(cursor.x - x);
rect.height = abs(cursor.y - y);
//防止矩形区域超出图像的范围
rect &= Rect(0, 0, src.cols, src.rows);
}
break;
}
}
int main()
{
src=imread(“test.jpg”);
if(!src.data)
{
cout《《“error, the image is not built!”《《endl;
return -1;
}
cvtColor(src, hsv, CV_BGR2HSV);
//用鼠标获取ROI
namedWindow(“SrcImage”);
imshow(“SrcImage”,hsv);
setMouseCallback(“SrcImage”, onMouse, NULL);
waitKey();
return 0;
}12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091
运行结果:
程序说明:
程序中涉及反向投影直方图的代码就几行而已,只是因为之前的博客中把直方图的计算封装成了类,就代码重用了[其实是懒]!再唠叨一句,反向投影直方图的结果是一个概率映射,其体现的是已知的图像内容出现在图像中特定位置的概率。
 电子发烧友App
电子发烧友App
























评论