FTW - 计算特定相位截断杂散的频率和幅度的方法

FTW中的L位位置取决于FTW的特定值(切记，FTW的值依据所需DDS输出频率而变化，详见公式1)。这种依赖性非常大，因为任意给定FTW的L位位置决定相位截断杂散在DDS输出频谱中的分配方式。

对于任意给定FTW，图3演示了如何找到L的值。首先，将FTW转换为二进制。然后，将指数值分配给FTW位，MSB的起始指数值为1。图3为一个32位FTW的示例；因此，指数范围为1至32。L值是值为1的最后一位的指数(从MSB向LSB读)。图3中的FTW值为0x0036e580(十六进制)，因此，采用本协议时，此特定FTW的L的值为25。

给定FTW的L的值最为重要。首先，L决定相位截断杂散是否出现在DDS输出频谱中。若L ≤ P，则没有相位截断杂散。若L > P，则包括PPT杂散在内的相位截断杂散出现在DDS输出频谱中。其次，L和P的值可确定PPT杂散的幅度和频率(假定L > P)。

PPT幅度

两个PPT杂散具有相同的幅度(见公式2)。 若已知特定FTW的值和给定DDS设计的P值，两个PPT杂散的幅度为：

 

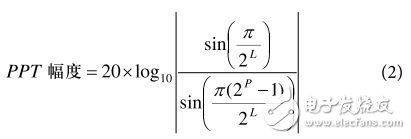
其中，PPT幅度的值以dBc为单位： 与频率为fO时主DDS输出信号的幅度相关的分贝。

请注意，公式2中的两个正弦函数的参数以弧度为单位。例如，假设DDS的P = 19，FTW如图3所示，则使用公式2得到的PPT杂散幅度为−114.38789 dBc。

PPT频率

需要多个步骤才能确定这两个PPT频率。第一步，得出K的值，FTW的十进制值截断为L位。要得到K，在FTW为二进制形式的情况下，消除尾随0并将得到的L位FTW转换为相应的十进制值。例如，图3中的FTW可得到K = 28,107(通过将二进制数字0000000000110110111001011转换为相应的十进制数字得出)。

使用K计算两个PPT杂散的频谱指数位置(R1和R2)，如下面的公式3和公式4所示：

例如，在DDS的P = 19且FTW如图3所示的情况下，公式3中括号内的数字为14,736,134,709，公式4中括号内的数字为928,378,285,515。将2 25 模数应用于这些值可得到

根据下面的公式5和公式6，使用R1和R2确定DDS输出频谱中的两个PPT频率位置(fPPT1和fPPT2)。

 

例如，若fS = 250 MHz，FTW如图3所示，且R1和R2的值已在前面的例子中计算出，则两个PPT杂散频率如下：
 

 

图3. FTW的L位

结论

尽管本应用笔记介绍了一种相对简单的方式来预测两个PPT杂散的频率和幅度，但公式3和公式4可能引起计算问题。具体而言，括号内的数字由一个整数定义，可能非常大。

为了解释这些计算中较大整数引起的问题，试重新考虑AD9912，其中N = 48，P = 19。假定FTW为0x400000000001(十六进制)，即70,368,744,177,665(十进制)。在此例中，L = 48；因此，K的值与FTW相同。

现在考虑公式4中括号内的数字。2L – 2P+ 1可得到以下值：
248 – 219 + 1 = 281,474,976,186,369

因此，由公式4中括号内的数字可得到
K × (2L – 2P+ 1) = 70,368,744,177,665 × 281,474,976,186,369
= 19,807,040,591,672,948,094,687,248,385

以二进制形式表示此整数需要94位。大部分计算软件工具无法精确表示这种大小的整数。例如，在64位机器上运行的MATLAB将K × (2 L– 2P + 1)表示为浮点数：1.980704059167295 × 1028。对应的整为19,807,040,591,672,950,000,000,000,000。此值与真实值偏差较大，因此得到的R2并不正确。

事实上，不仅大部分软件工具无法处理极大整数，而且大部分计算机内部的处理器芯片也无法处理极大整数。例如，一台带64位处理器的计算机无法处理94位整数。这个问题至关重要，因为计算R1和R2值需要极大整数计算，这超出了大部分计算机的能力。

除了正确表示公式3和公式4中括号内的数字，还需要计算括号内数字的2L模数。在前面的例子中，L = 48，这意味着模数达48位。大部分计算机不支持超过32位的模数计算。

总而言之，公式3和公式4产生的难题在使用软件工具实现PPT杂散计算时需要特别注意。用户必须将括号内的数字作为一个整数进行正确计算(无截断或四舍五入)，并且应在不损失精度的情况下正确处理模数计算。

尽管大部分软件工具和处理器无法直接处理极大整数，但也有例外。例如，软件工具Python本身支持极大整数计算。尽管MATLAB®本身无法处理极大整数，但支持极大整数计算的可变精度整数(VPI)工具箱可在MATLAB Central的Math Works网站上免费下载。