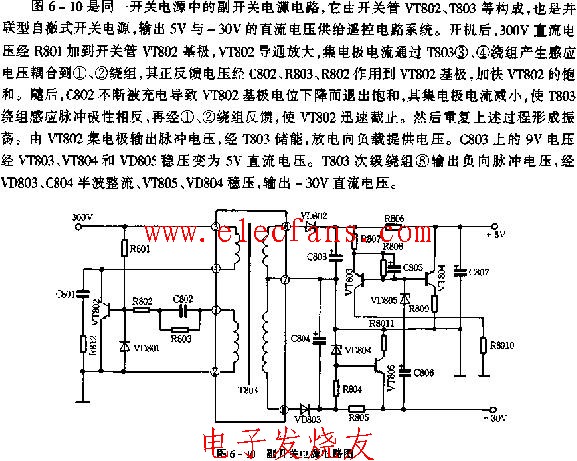
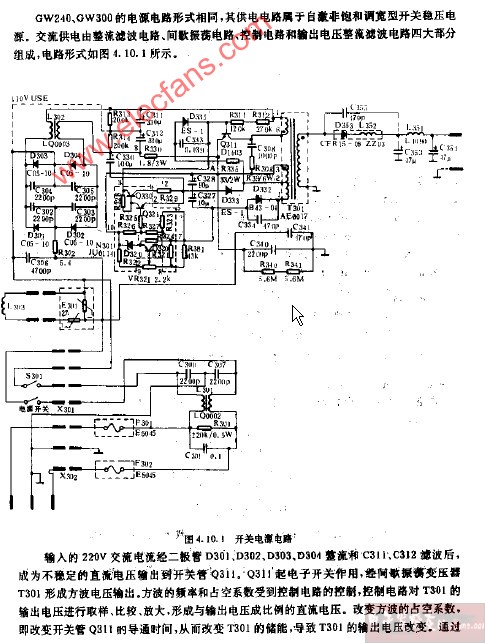
秘笈三 阻尼输入滤波系列第一部分 - 开关电源电路开发设计秘籍大全

　　秘笈三 阻尼输入滤波系列第一部分

　　开关调节器通常优于线性调节器，因为它们更高效，而开关拓扑结构则十分依赖输入滤波器。 这种电路元件与电源的典型负动态阻抗相结合， 可以诱发振荡问题。本文将阐述如何避免此类问题的出现。

　　一般而言，所有的电源都在一个给定输入范围保持其效率。因此，输入功率或多或少地与输入电压水平保持恒定。 图3.1显示的是一个开关电源的特征。 随着电压的下降，电流不断上升。

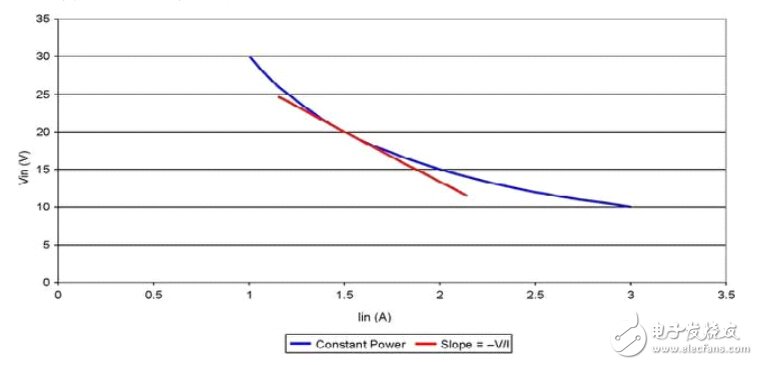
　　图3.1 开关电源表现出的负阻抗

　　负输入阻抗

　　电压-电流线呈现出一定的斜率， 其从本质上定义了电源的动态阻抗。 这根线的斜率等于负输入电压除以输入电流。 也就是说， 由Pin=V•， 可以得出V=Pin/I； 并由此可得dV/dI=–Pin/I2或dV/dI≈–V/I。

　　该近似值有些过于简单，因为控制环路影响了输入阻抗的频率响应。但是很多时候，当涉及电流模式控制时这种简单近似值就已足够了。

　　为什么需要输入滤波器

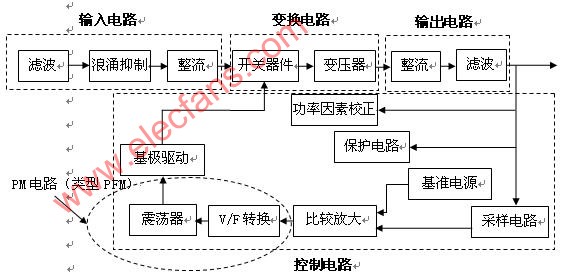
　　开关调节器输入电流为非连续电流，并且在输入电流得不到滤波的情况下其会中断系统的运行。 大多数电源系统都集成了一个如图3.2所示类型的滤波器。 电容为功率级的开关电流提供了一个低阻抗，而电感则为电容上的纹波电压提供了一个高阻抗。该滤波器的高阻抗使流入源极的开关电流最小化。在低频率时，该滤波器的源极阻抗等于电感阻抗。在您升高频率的同时，电感阻抗也随之增加。在极高频率时，输出电容分流阻抗。在中间频率时，电感和电容实质上就形成了一种并联谐振电路，从而使电源阻抗变高，呈现出较高的电阻。

　　大多数情况下，峰值电源阻抗可以通过首先确定滤波器 （Zo） 的特性阻抗来估算得出，而滤波器特性阻抗等于电感除以电容所得值的平方根。这就是谐振下电感或者电容的阻抗。 接下来， 对电容的等效串联电阻 （ESR） 和电感的电阻求和。 这样便得到电路的Q值。峰值电源阻抗大约等于Zo乘以电路的Q值。

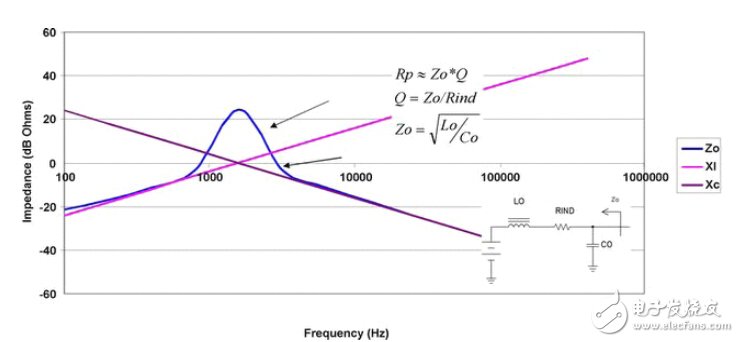
　　图3.2 谐振时滤波器的高阻抗和高阻性

　　振荡

　　但是， 开关的谐振滤波器与电源负阻抗耦合后会出现问题。 图3.3显示的是在一个电压驱动串联电路中值相等、极性相反的两个电阻。这种情况下，输出电压趋向于无穷大。当您获得由谐振输入滤波器等效电阻所提供电源的负电阻时，您也就会面临一个类似的电源系统情况；这时，电路往往就会出现振荡。

　　图3.3 与其负阻抗耦合的开关谐振滤波器可引起不必要的振荡

　　设计稳定电源系统的秘诀是保证系统电源阻抗始终大大小于电源的输入阻抗。我们需要在最小输入电压和最大负载（即最低输入阻抗）状态下达到这一目标。

　　秘笈四 阻尼输入滤波系列第二部分

　　控制源极阻抗

　　在“电源设计秘笈3”中， 我们讨论了输入滤波器的源极阻抗如何变得具有电阻性，以及其如何同开关调节器的负输入阻抗相互作用。在极端情况下，这些阻抗振幅可以相等，但是其符号相反从而构成了一个振荡器。业界通用的标准是输入滤波器的源极阻抗应至少比开关调节器的输入阻抗低6dB， 作为最小化振荡概率的安全裕度。

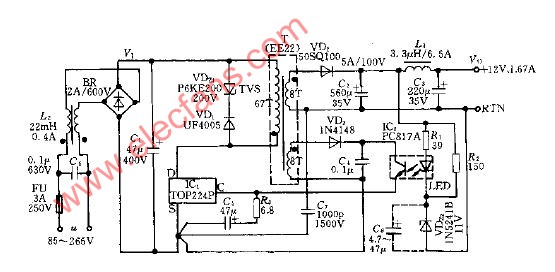
　　输入滤波器设计通常以根据纹波电流额定值或保持要求选择输入电容（图4.1所示CO）开始的。第二步通常包括根据系统的EMI要求选择电感 （LO）。正如我们上个月讨论的那样，在谐振附近，这两个组件的源极阻抗会非常高，从而导致系统不稳定。 图 1 描述了一种控制这种阻抗的方法， 其将串联电阻 （RD） 和电容 （CD） 与输入滤波器并联放置。利用一个跨接 CO 的电阻，可以阻尼滤波器。但是，在大多数情况下，这样做会导致功率损耗过高。另一种方法是在滤波器电感的两端添加一个串联连接的电感和电阻。

　　图4.1 CD和RD阻尼输出滤波器源极阻抗

　　选择阻尼电阻

　　有趣的是，一旦选择了四个其他电路组件，那么就会有一个阻尼电阻的最佳选择。图4.2 显示的是不同阻尼电阻情况下这类滤波器的输出阻抗。红色曲线表示过大的阻尼电阻。请思考一下极端的情况，如果阻尼电阻器开启，那么峰值可能会非常的高，且仅由CO和LO来设定。蓝色曲线表示阻尼电阻过低。如果电阻被短路，则谐振可由两个电容和电感的并联组合共同设置。绿色曲线代表最佳阻尼值。利用一些包含闭型解的计算方法（见参考文献 1）就可以很轻松地得到该值。

　　图4.2 在给定CD-CO比的情况下，有一个最佳阻尼电阻

　　选择组件

　　在选择阻尼组件时，图4.3非常有用。该图是通过使用RD Middlebrook建立的闭型解得到的。横坐标为阻尼滤波器输出阻抗与未阻尼滤波器典型阻抗 （ZO=（LO/CO）1/2） 的比。 纵坐标值有两个： 阻尼电容与滤波器电容 （N） 的比； 以及阻尼

　　电阻同该典型阻抗的比。 利用该图， 首先根据电路要求来选择LO和CO， 从而得到ZO。

　　随后，将最小电源输入阻抗除以二，得到您的最大输入滤波器源极阻抗 （6dB）。最小电源输入阻抗等于Vinmin2/Pmax。只需读取阻尼电容与滤波器电容的比以及阻尼电阻与典型阻抗的比， 您便可以计算得到一个横坐标值。例如，一个具有10μH电感和10μH 电容的滤波器具有Zo= （10μH/10μF）1/2=1Ohm 的典型阻抗。 如果它 正对 一个 12V 最 小输 入的 12W 电 源进 行滤 波， 那么 该电 源输 入阻 抗将 为Z=V2/P=122/12=12Ohms。这样，最大源极阻抗应等于该值的二分之一，也即6Ohms。

　　现在，在6/1=6的X轴上输入该图，那么，CD/CO=0.1，即1μF，同时RD/ZO=3，也即3Ohms。

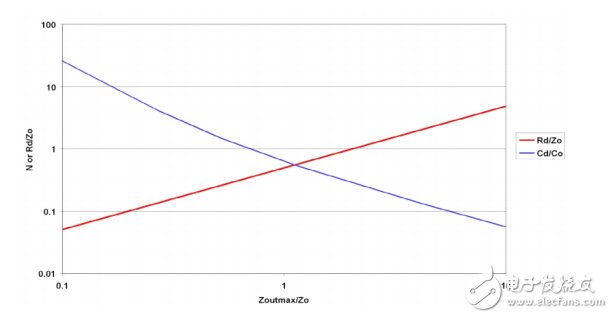
　　图4.3 选取LO和CO后，便可从最大允许源极阻抗范围内选择CD和RD

　　秘笈五 降压—升压电源设计中降压控制器的使用

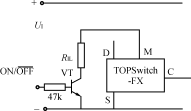
　　电子电路通常都工作在正稳压输出电压下，而这些电压一般都是由降压稳压器来提供的。如果同时还需要负输出电压，那么在降压—升压拓扑中就可以配置相同的降压控制器。负输出电压降压—升压有时称之为负反向，其工作占空比为50%， 可提供相当于输入电压但极性相反的输出电压。其可以随着输入电压的波动调节占空比，以“降压”或“升压”输出电压来维持稳压。

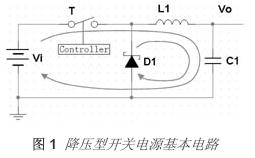
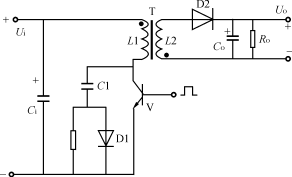
　　图 5.1显示了一款精简型降压—升压电路，以及电感上出现的开关电压。这样一来该电路与标准降压转换器的相似性就会顿时明朗起来。实际上，除了输出电压和接地相反以外，它和降压转换器完全一样。这种布局也可用于同步降压转换器。这就是与降压或同步降压转换器端相类似的地方，因为该电路的运行与降压转换器不同。

　　FET开关时出现在电感上的电压不同于降压转换器的电压。 正如在降压转换器中一样， 平衡伏特-微秒 （V-μs） 乘积以防止电感饱和是非常必要的。 当FET为开启时（如图 1 所示的ton间隔），全部输入电压被施加至电感。这种电感“点”侧上的正电压会引起电流斜坡上升， 这就带来电感的开启时间V-μs乘积。 FET 关闭 （toff）期间，电感的电压极性必须倒转以维持电流，从而拉动点侧为负极。电感电流斜坡下降， 并流经负载和输出电容， 再经二极管返回。 电感关闭时V-μs乘积必须等于开启时V-μs乘积。由于Vin和Vout不变，因此很容易便可得出占空比 （D） 的表达式：

　　D=Vout/（Vout “ Vin）。 这种控制电路通过计算出正确的占空比来维持输出电压稳压。

　　上述表达式和图5.1所示波形均假设运行在连续导电模式下。

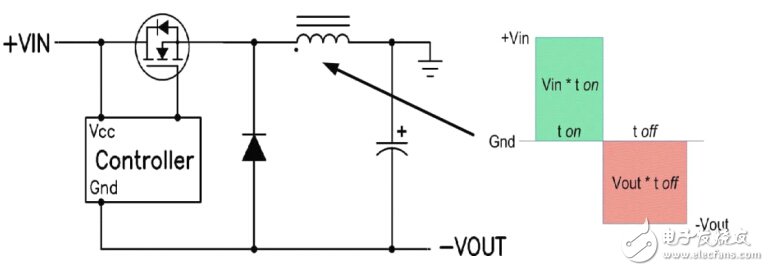
　　图 5.1 降压—升压电感要求平衡其伏特-微秒乘积

　　降压 — 升压电感必须工作在比输出负载电流更高的电流下。其被定义为IL=I《SUBOUT《 sub》/（1-D），或只是输入电流与输出电流相加。对于和输入电压大小相等的负输出电压（D =0.5）而言，平均电感电流为输出的2倍。

　　有趣的是，连接输入电容返回端的方法有两种，其会影响输出电容的rms电流。典型的电容布局是在 +Vin 和 Gnd 之间，与之相反，输入电容可以连接在 +Vin 和”V《SUBOUT《 sub》 之间。利用这种输入电容配置可降低输出电容的rms电流。然而，由于输入电容连接至 “Vout，因此 ”Vout上便形成了一个电容性分压器。这就在控制器开始起作用以前， 在开启时间的输出上形成一个正峰值。 为了最小化这种影响，最佳的方法通常是使用一个比输出电容要小得多的输入电容， 请参见图5.2所示的电路。输入电容的电流在提供dc输出电流和吸收平均输入电流之间相互交替。rms 电流电平在最高输入电流的低输入电压时最差。因此，选择电容器时要多加注意，不要让其ESR过高。陶瓷或聚合物电容器通常是这种拓扑较为合适的选择。

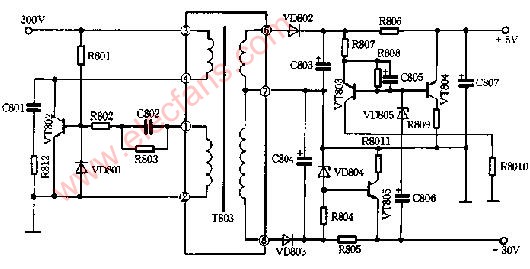
　　图5.2 降压控制器在降压—升压中的双重作用

　　必须要选择一个能够以最小输入电压减去二极管压降上电的控制器，而且在运行期间还必须能够承受得住Vin加Vout的电压。FET和二极管还必须具有适用于这一电压范围的额定值。通过连接输出接地的反馈电阻器可实现对输出电压的调节，这是由于控制器以负输出电压为参考电压。只需精心选取少量组件的值，并稍稍改动电路，降压控制器便可在负输出降压—升压拓扑中起到双重作用。