可再配置PLL的最佳配置 - 全文

引言

在开始查找PLL的最佳配置之前，需要考虑的是如何才能为PLL找到配置。具体而言，我们应找到PLL针对给定参考振荡器和所需输出频率所使用的所有可行配置。只有在确保获得能够满足需要的全部可行配置列表之后，我们才能确定哪一种树最好的。实际上，明确最佳PLL配置的大部分工作都涉及如何找到满足我们需求的全部可行配置列表。有鉴于此，本文将首先集中讨论所有可行的配置，然后再找出最佳的选择方案。

整数除PLL频率合成概述

从最基本的角度而言，任何频率合成器都旨在根据给定的参考频率生成所需的输出频率，即如下所示：

                        （1）

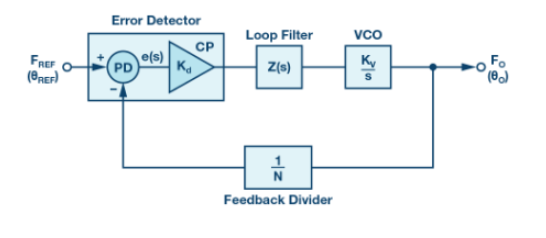
其中，κ代表的是指频率定标常量，有时也被视作标准频率。任何频率合成器电路都是一种趋近于κ的机制。概括介绍生成κ的方法不在本文的讨论范畴之内（不过今后可以撰文加以介绍）。我们在本文中将专门讨论整数除PLL频率合成器。PLL频率合成器在参考振荡器和输出时钟之间插入分隔块以趋近于κ。然后使用带有相位侦测器的反馈回路在两个分隔器之间保持相位相干性，最终生成所需的输出频率。相关的方框图如图1所示。该图显示了一种通用式充电泵整数除锁相回路。

三个分隔块用来趋近κ值：参考分隔器（Q）、反馈分隔器（P）和输出分隔器（N）。我们很容易就能看出，针对此类频率合成器，k的定义为：

                            （2）


图1. 基本整数除PLL的方框图

结合方程式1和方程式2，我们可得出输入和输出频率之间的关系：

                    （3） 

图1所示通用式的一般变体是将N设为1，Q设为1，或二者皆设为1的形式。这些都是根据系统设计需要而简化的。对这三种简化形式的分析是图1所示一般情况的一个子集。如果Q和N都设为1，那么输出频率的最大分辨率限定于参考频率，这样我们就只能合成整数参考倍数。在此情况下，P值的确定就成了较简单的算术问题。如果Q或N设为1，那么合成所需输出只存在单一的配置（最小Q/P或N/P比）。这时需要进行约分才能确定比值。

使用全部三个分隔块会给硬件增加一个通用层，可以通过对许多不同频率合成应用编程而直接重用PLL。不过，这种通用性也导致确定P、Q和N的使用值极为困难。具体而言，这会造成单个参考和输出频率存在多种配置，而且所有这些配置都有着极为不同的性能特点（功耗、启动时间、抖动、相位噪声等）。

可编程SoC中使用的另一种配置方法是采用多个输出分隔器，这能生成多个不同频率的输出（不过仍是VCO频率的整数倍数）。图2显示的是这种配置的具体情况。 



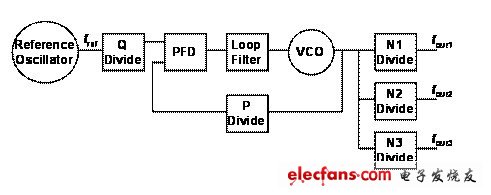
图2. 带多个输出分隔器的基本整数除PLL方框图

为可编程PLL查找所有可行的配置 

那么，就给定的一系列系统要求而言，我们如何选择P、Q和N的分隔值呢？首先，我们讨论一下稍微改变一下方程式3的一种变体：把所有已知的值放在右边，所有未知的值放在左边：

                        （4）

对任意参考和输出频率来说，求解方程式4的难点是存在三级自由度（仅由P、Q和N可能的分隔值范围决定）。求解方程式4最常见的办法就是采取搜索算法。这种算法会搜索解决方案空间，查找获得所需值的P、Q和N值集合。这种算法本质上属于搜索所有可行P、Q和N值的三嵌套回路。大多数PLL配置软件都在使用这种搜索算法。图3显示的是这种算法实施方法的概念伪码。请注意，为了仅可靠地生成有用配置，需要为该代码添加许多实际的系统约束。

Figure 3.  Pseudo code for calculating divide values

图3. 计算分隔值的伪码

for n=Nmin; n < Nmax; n++ 
    for q=Qmin; q < Qmax; q++
        for p=Pmin; p < Pmax; p++
            if p /（q*n）==（fout/fref）
                save [p,q,n]
            else
                continue
示例 

我们在示例中将从14.3181818…MHz参考（常见的视频应用频率）中合成50MHz输出。假定VCO的频率范围为100MHz到400MHz。我们使用类似于图3所示的搜索算法，可生成如表1所示的结果。该表列出了满足我们需要的所有可行配置。现在，我们需要从中选出“最佳”选择。

 

Table 1.  Summary of Example Results 表1. 示例结果汇总
N	Fref [MHz]	fvco [MHz]	Fout [MHz]	fpfd [MHz]	Q	P
2	14.318…	100	50	0.227	63	440
3	14.318…	150	50	0.682	21	220
4	14.318…	200	50	0.227	63	880
5	14.318…	250	50	0.227	63	1100
6	14.318…	300	50	0.682	21	440
7	14.318…	350	50	1.591	9	220
8	14.318…	400	50	0.227	63	1760

选择最佳配置 

我们现在已经找到了满足频率需求的所有配置，接下来将集中精力选择“最佳”配置。“最佳”配置完全取决于不同的应用。就远程监控站而言，我们需要快速唤醒部件，但对准确度的要求不是太高。对通信协议而言，我们不太在意启动时间或功耗，只需要极低的抖动时钟源。当然我们也可能同时面临着两种应用需求。在数据采集阶段，我们可能只需要快速唤醒功能，而在数据传输阶段，则需要较高的准确度。利用可编程PLL和可编程SoC，我们可以同时实现上述两种要求，但前提条件是知道采用哪种配置。 

我们将在此讨论针对不同应用而优化的几种常见PLL参数。表2总结了这些参数、相应的关键回路参数、以及优化方法。请注意，不是所有的可编程PLL都能为您提供以上所列出的全部参数。

功耗

功耗取决于VCO频率、充电泵电流和分隔块的设置。大多数VCO架构都要求较大的末端电流来提高频率。因此，随着频率的升高，功耗也会增加。每个PFD期间都会有一次充电泵电流放电。如果需要更高的充电泵电流（满足回路稳定或快速启动/稳定时间的要求），则每个PFD期间功耗的更高。时钟分隔器在每个时钟脉冲边沿都会消耗功耗。时钟分隔值越高，则需要更多的分隔单元进行转换，这也增加了功耗。

启动时间 / 稳定时间

充电泵PLL的启动和稳定时间取决于回路自然频率。该参数可视为PLL的频率转换速率，它对PLL改变输出频率的速度加以量化。它同VCO增益和充电泵电流成正比，而与反馈分隔值和回路滤波器电容成反比。为了最小化启动时间，我们应最大化VCO增益和充电泵电流，并最小化反馈分隔设置和回路滤波器电容。

抖动

与启动时间/稳定时间一样，PFD频率和VCO增益也会对抖动产生很大影响。PFD频率越高，就意味着PLL回路滤波器电压刷新的频率越高。这会避免回路滤波器电压漂移。使用回路滤波器电容，每个PFD期间的电压漂移量可以最小化。由于VCO增益决定着回路滤波器上单位电压漂移的输出频率漂移量，因此降低VCO增益可降低PLL对回路滤波器电压漂移的敏感度。

相位噪声

优化相位噪声与具体的应用密切相关，但我们这里还是要指出以下问题。一般而言，我们可将PLL设为较低的闭环带宽，从而抑制参考振荡器产生的相噪声，设置PLL为较高的闭环带宽则能抑制VCO产生的相噪声。

我们还可通过控制输出分隔器（N）这一参数来降低相位噪声。相位噪声分隔与输出分隔的设置相关。如果输出分隔器为低噪声分隔器，那么运行高频VCO并分隔输出频率将改进相位噪声性能。

 

 

 

表2. 可编程PLL的优化参数
参数	关键回路参数	优化
功耗	VCO频率（fvco） 充电泵电流（Ichp） 分隔值（P, Q, N）	最小化fvco 最小化Ichp 最小化P, Q, N
启动时间 / 稳定时间	PFD频率（fpfd） 充电泵电流（Ichp） 回路滤波器电容（C） VCO增益（Kvco）	最大化fpfd 最大化Ichp 最小化C 最大化Kvco
抖动 （循环间）	PFD频率（fpfd） 回路滤波器电容（C） VCO增益（Kvco）	最大化fpfd 最大化C 最小化Kvco
相位噪声	闭环带宽 PLL组件相位噪声 输出分隔器（N）	最大化fvco 最大化N 用闭环带宽抑制参考噪声和VCO噪声。

优化示例 

最后，我们将上述通用性优化措施应用于上例中找出的一系列PLL配置。

功耗

如果设计的主要目的是确保低功耗，那么我们应最小化VCO频率和分隔值，因此选择N=3、Q=21、P=220将是最佳选择。这时，VCO频率较低，P和Q的值较低，而且PFD频率也比较合理。

启动 / 稳定时间

如果我们主要关切启动/稳定时间，那么从表1中我们可以明显看出，N=7、Q=9、P=220是最佳选择。这时，f_PFD超过其他配置的两倍以上，从而提升回路滤波器电压的刷新率。

抖动

如果我们主要关切低抖动，那么N=7、Q=9、P=220仍是最佳选择。这时，f_PFD比其他配置高出两倍多，从而让回路滤波器电压的刷新率得以提升，并实现所有可能配置中的最低抖动。差别在于我们应当为低抖动选择较大的回路滤波器电容和较低的K_vco。

相位噪声

优化相位噪声在很大程度上取决于不同的应用以及具体的参考振荡器和VCO噪声性能。我们根据配置列表可做的一个设计选择就是选用经过分隔的较高VCO频率。N=7、Q=9、P=220可能是最佳选择，因为其PFD频率大大高于N=8、Q=63、P=1760时的PFD频率。如果回路的抖动较高，将大幅提高相位噪声水平，进而会抵消输出分隔器所带来的任何收益。