函数 - Python机器学习回归部分的应用与教程

现在我们要开始填充函数了。
def create_dataset(hm,variance,step=2,correlation=False):
val = 1
ys = []
for i in range(hm):
y = val + random.randrange(-variance,variance)
ys.append(y)

非常简单，我们仅仅使用hm变量，迭代我们所选的范围，将当前值加上一个负差值到证差值的随机范围。这会产生数据，但是如果我们想要的话，它没有相关性。让我们这样：
def create_dataset(hm,variance,step=2,correlation=False):
val = 1
ys = []
for i in range(hm):
y = val + random.randrange(-variance,variance)
ys.append(y)
if correlation and correlation == 'pos':
val+=step
elif correlation and correlation == 'neg':
val-=step

非常棒了，现在我们定义好了 y 值。下面，让我们创建 x，它更简单，只是返回所有东西。
def create_dataset(hm,variance,step=2,correlation=False):
val = 1
ys = []
for i in range(hm):
y = val + random.randrange(-variance,variance)
ys.append(y)
if correlation and correlation == 'pos':
val+=step
elif correlation and correlation == 'neg':
val-=step

xs = [i for i in range(len(ys))]

return np.array(xs, dtype=np.float64),np.array(ys,dtype=np.float64)

我们准备好了。为了创建样例数据集，我们所需的就是：
xs, ys = create_dataset(40,40,2,correlation='pos')

让我们将之前线性回归教程的代码放到一起：
from statistics import mean
import numpy as np
import random
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')

def create_dataset(hm,variance,step=2,correlation=False):
val = 1
ys = []
for i in range(hm):
y = val + random.randrange(-variance,variance)
ys.append(y)
if correlation and correlation == 'pos':
val+=step
elif correlation and correlation == 'neg':
val-=step

xs = [i for i in range(len(ys))]

return np.array(xs, dtype=np.float64),np.array(ys,dtype=np.float64)

def best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))

b = mean(ys) - m*mean(xs)

return m, b

def coefficient_of_determination(ys_orig,ys_line):
y_mean_line = [mean(ys_orig) for y in ys_orig]

squared_error_regr = sum((ys_line - ys_orig) * (ys_line - ys_orig))
squared_error_y_mean = sum((y_mean_line - ys_orig) * (y_mean_line - ys_orig))

print(squared_error_regr)
print(squared_error_y_mean)

r_squared = 1 - (squared_error_regr/squared_error_y_mean)

return r_squared

xs, ys = create_dataset(40,40,2,correlation='pos')
m, b = best_fit_slope_and_intercept(xs,ys)
regression_line = [(m*x)+b for x in xs]
r_squared = coefficient_of_determination(ys,regression_line)
print(r_squared)

plt.scatter(xs,ys,color='#003F72', label = 'data')
plt.plot(xs, regression_line, label = 'regression line')
plt.legend(loc=4)
plt.show()

执行代码，你会看到：

 

判定系数是 0.516508576011（要注意你的结果不会相同，因为我们使用了随机数范围）。

不错，所以我们的假设是，如果我们生成一个更加紧密相关的数据集，我们的 R 平方或判定系数应该更好。如何实现它呢？很简单，把范围调低。
xs, ys = create_dataset(40,10,2,correlation='pos')

 

 

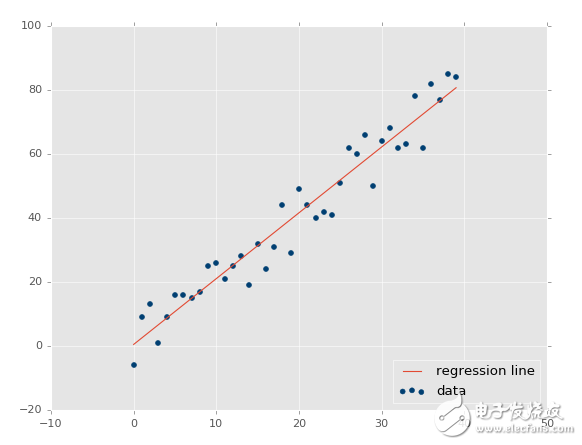
现在我们的 R 平方值为 0.939865240568，非常不错，就像预期一样。让我们测试负相关：

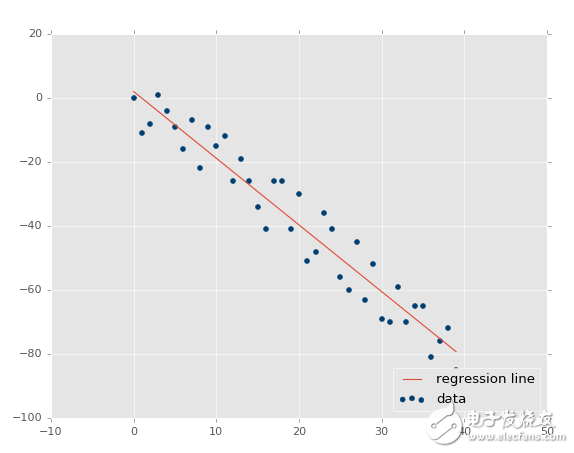
xs, ys = create_dataset(40,10,2,correlation='neg')

 

R 平方值是 0.930242442156，跟之前一样好，由于它们参数相同，只是方向不同。

这里，我们的假设证实了：变化越小 R 值和判定系数越高，变化越大 R 值越低。如果是不相关呢？应该很低，接近于 0，除非我们的随机数排列实际上有相关性。让我们测试：
xs, ys = create_dataset(40,10,2,correlation=False)

 

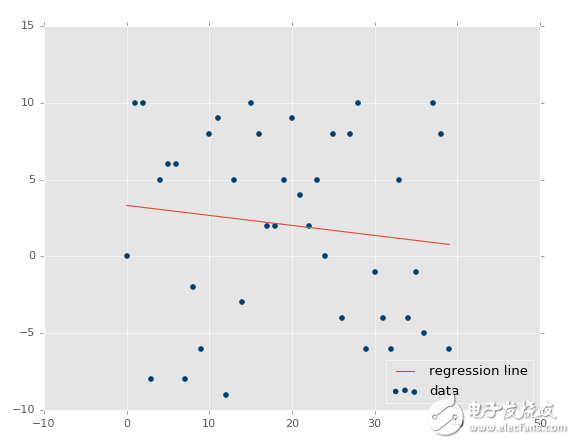
判定系数为 0.0152650900427。

现在为止，我觉得我们应该感到自信，因为事情都符合我们的预期。

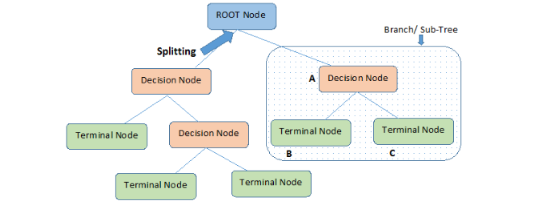
既然我们已经对简单的线性回归很熟悉了，下个教程中我们开始讲解分类。