计算纵截距 - Python机器学习回归部分的应用与教程

下面干什么？我们需要计算纵截距b。我们会在下一个教程中处理它，并完成完整的最佳拟合直线计算。它比斜率更佳易于计算，尝试编写你自己的函数来计算它。如果你做到了，也不要跳过下一个教程，我们会做一些别的事情。

计算纵截距

欢迎阅读第九篇教程。我们当前正在为给定的数据集，使用 Python 计算回归或者最佳拟合直线。之前，我们编写了一个函数来计算斜率，现在我们需要计算纵截距。我们目前的代码是：
from statistics import mean
import numpy as np

xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)

def best_fit_slope(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))
return m

m = best_fit_slope(xs,ys)
print(m)

请回忆，最佳拟合直线的纵截距是：

这个比斜率简单多了。我们可以将其写到同一个函数来节省几行代码。我们将函数重命名为best_fit_slope_and_intercept。

下面，我们可以填充b = mean(ys) - (m*mean(xs))，并返回m, b：
def best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))

b = mean(ys) - m*mean(xs)

return m, b

现在我们可以调用它：
best_fit_slope_and_intercept(xs,ys)

我们目前为止的代码：
from statistics import mean
import numpy as np

xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)

def best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))

b = mean(ys) - m*mean(xs)

return m, b

m, b = best_fit_slope_and_intercept(xs,ys)

print(m,b)
# 0.3, 4.3

现在我们仅仅需要为数据创建一条直线：

 

要记住y=mx+b，我们能够为此编写一个函数，或者仅仅使用一行的for循环。
regression_line = [(m*x)+b for x in xs]

上面的一行for循环和这个相同：
regression_line = []
for x in xs:
regression_line.append((m*x)+b)

好的，让我们收取我们的劳动果实吧。添加下面的导入：
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')

我们可以绘制图像，并且不会特备难看。现在：
plt.scatter(xs,ys,color='#003F72')
plt.plot(xs, regression_line)
plt.show()

首先我们绘制了现有数据的散点图，之后我们绘制了我们的回归直线，之后展示它。如果你不熟悉，可以查看 Matplotlib 教程集。

输出：

 

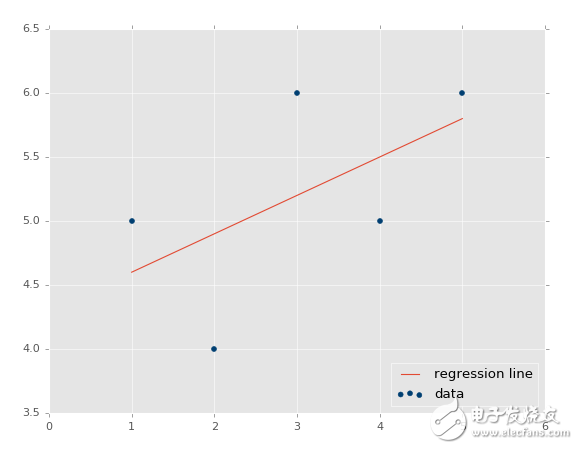
所以，如何基础这个模型来做一些实际的预测呢？很简单，你拥有了模型，只要填充x就行了。例如，让我们预测一些点：
predict_x = 7

我们输入了数据，也就是我们的特征。那么标签呢？
predict_y = (m*predict_x)+b
print(predict_y)
# 6.4

我们也可以绘制它：
predict_x = 7
predict_y = (m*predict_x)+b

plt.scatter(xs,ys,color='#003F72',label='data')
plt.plot(xs, regression_line, label='regression line')
plt.legend(loc=4)
plt.show()

输出：

 

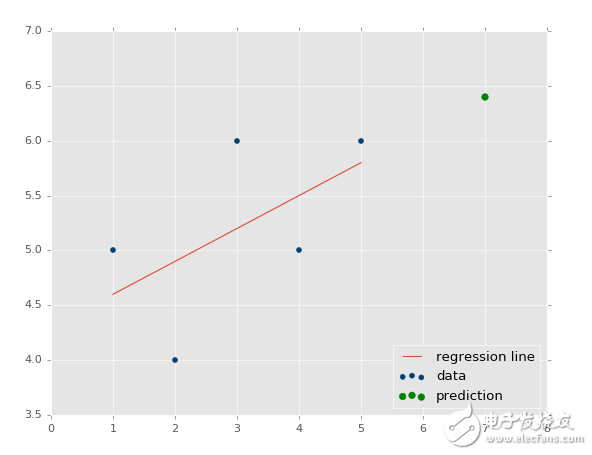
我们现在知道了如何创建自己的模型，这很好，但是我们仍旧缺少了一些东西，我们的模型有多精确？这就是下一个教程的话题了。

R 平方和判定系数原理

欢迎阅读第十篇教程。我们刚刚完成了线性模型的创建和处理，现在我们好奇接下来要干什么。现在，我们可以轻易观察数，并决定线性回归模型有多么准确。但是，如果你的线性回归模型是拿神经网络的 20 个层级做出来的呢？不仅仅是这样，你的模型以步骤或者窗口工作，也就是一共 5 百万个数据点，一次只显示 100 个，会怎么样？你需要一些自动化的方式来判断你的最佳拟合直线有多好。

回忆之前，我们展示几个绘图的时候，你已经看到，最佳拟合直线好还是不好。像这样：

 

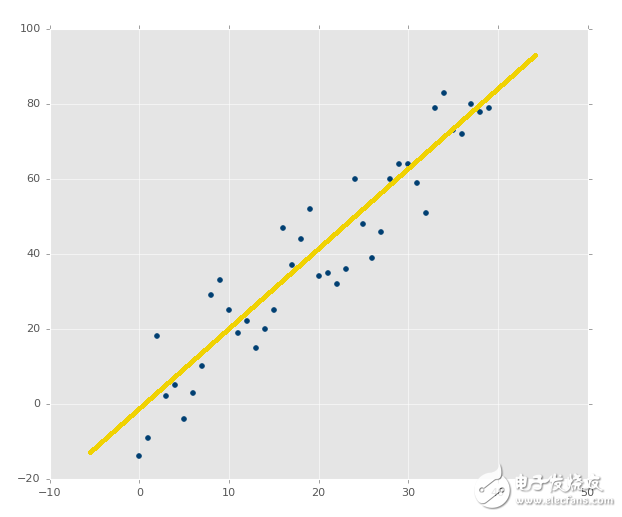
与这个相比：

 

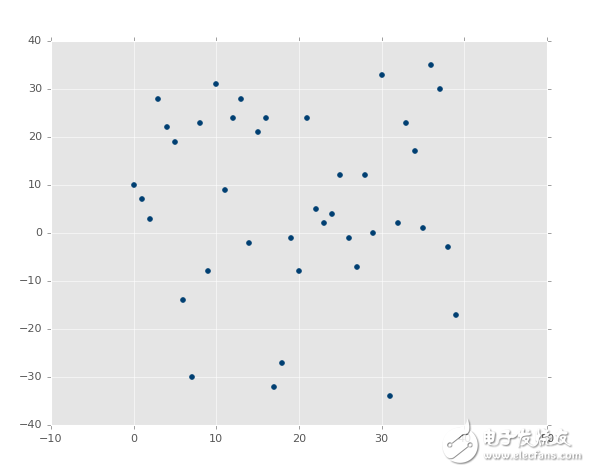
第二张图片中，的确有最佳拟合直线，但是没有人在意。即使是最佳拟合直线也是没有用的。并且，我们想在花费大量计算能力之前就知道它。