回到正题:图灵机。图灵机能够识别语言,而图灵机本身当然也可以由语言描述。什么是语言?给定一个字母表∑,一个{[由∑中的字母组成的序列]的集合}就是∑上的一个语言(为了消除歧义,算式可以加括号,语言当然也可以)。必须清楚这些概念中哪些是有限的,哪些是无限的:一个语言包含的字符串数可以是有限的也可以是无限的,但一个字母表上的所有语言的数目是无限的,而语言中任意一个字符串的长度是有限的。
首先要证明的是:一个字母表上所有语言构成的集合不仅是无限的,而且是不可数的。 这里需要借助无限二进制序列的集合来帮助证明。一个无限二进制序列(即{0,1}组成的无限序列)是一阶无限,那么这些序列组成的集合就是“无限×无限”,可以通过对角线方法证明无限二进制序列是不可数的,也可以将实数集的元素唯一地映射到无限二进制序列集合。
用后者的方法,可以这样建立二者之间的映射:二进制序列每4个为一组,用8421BCD码编码,4位对应实数中的一位,再用1111表示小数点,这样每个实数总能映射到一个唯一的二进制序列,既然实数集不可数,那么无限二进制序列也不可数。 接下来证明,{无限二进制序列的集合B}与(任意字母表){∑上的所有语言组成的集合L}是同样规模的,仍然通过建立映射的方法。设∑上所有字符串的集合按字典序排序成∑*={s1, s2, s3, 。..},L中的每个语言A都对应一个二进制序列b:如果si∈A,bi=1;否则bi=0,这样的序列称作A的特征序列。举个例子,如果∑={a,b},A是所有包含b的串构成的语言,则A的特征序列b如下:
∑*={a, b, aa, ab, ba, bb, aaa, aab,。..} A ={ b, ab, ba, bb, aab,。..} b = 0 1 0 1 1 1 0 1 ,。..
反之,每个二进制序列b也能对应一个唯一的语言,所以L与B等势,又因为B是不可数集,所以{∑上的所有语言组成的集合L}也是不可数的。
好,明确了所有语言构成的集合是不可数的之后,我要回答下面这个问题:为什么图灵机集合是可数的?(reserve:哥德尔配数法)
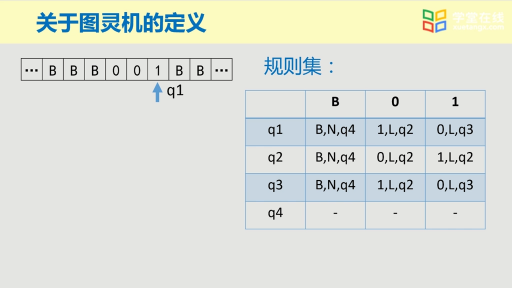
从图灵机的定义入手,图灵机是1个7元组(Q,∑,Γ,δ,q0,qaccept,qreject)。每一台图灵机总是由有限个字符编码而成: 1) 有限的状态集Q。 2) 有限的输入字母表∑。 3) 有限的带字母表Γ。 4) 有限的转换函数δ。 5) 1个起始状态q0。 6) 有限个接受状态qaccept。 7) 有限个拒绝状态qreject。 若上述每个元素都用二进制编码表示,任意一台图灵机都只需要有限个二进制位。再将这些二进制串按照字典序排列,就可以得到一个{图灵机集合}-》自然数集的一一对应。
好,给定一个字母表∑: [∑上的所有语言]的集合《=》[二进制无限序列]的集合《=》实数集《=》不可数集 [所有图灵机]的集合《=》自然数集《=》可数集
有不可数个语言,却只有可数个图灵机,语言的集合“大于”图灵机的集合,所以从本质上证明了必然存在图灵机不能识别的语言。 推论:必然存在图灵机不能判定的语言。理由是图灵可判定语言的集合不会大于图灵可识别语言。 图灵可判定语言要求更严格,所以应该存在这样的语言:它是图灵可识别的,但同时不是图灵可判定的。事实确实如此,图灵自己就给出了一个: A={《M, ω》 | M描述一台图灵机,且M描述的机器接受ω} 首先证明A是图灵可识别的(形式化证明太过繁琐,这里只给出很高层次的证明)。设通用图灵机U这样运行:U接受参数《M, ω》,它可根据图灵机M的描述模拟M的行为,并在虚拟的M上计算ω。如果M接受ω,那么U进入接受状态;否则拒绝。
依据定义以及通用图灵机的存在性,U能识别A,所以A是图灵可识别的,证毕。
顺着这个证明走下去,如果M本身遇到输入ω时会陷入循环,那么模拟M的U也会陷入循环,所以U不是判定器。如果U知道M在ω上不停机,那么它可以进入拒绝状态,问题是它不知道。那么能判定A的图灵机存在吗?我们就假设存在H,使得: 1)若M接受ω,则H(《M,ω》) =接受 2)若M不接受ω,则H(《M,ω》) =拒绝 根据H的定义,无论M接不接受ω,H总能停机。进一步再假设有图灵机D,以H为子程序,接受一个描述图灵机的串《M》,在H上运行H(《M,《M》》),并返回相反的结果: 1)若H(《M,《M》》)=接受,则D(《M》)=拒绝 2)若H(《M,《M》》) =拒绝,则D(《M》)=接受 也就是说,如果一台图灵机M接受描述它自身的串《M》,那么D(《M》)进入拒绝状态。构造这样一台奇怪的D是为了让它做下面这件事情,现在对D输入描述它自己的串《D》,看看会发生什么: 1)若D接受《D》,即H(《D,《D》》)=接受,则D(《D》)=拒绝 2)若D拒绝《D》,即H(《D,《D》》) =拒绝,则D(《D》)=接受 到底是接受还是拒绝呢?兜了一个圈子,D绕回原地,产生了矛盾。所以D是不存在的,所以H也是不存在的,语言A不可判定,证毕。
上述证明比较绕,我用一阶逻辑再改写一遍
命题: 1)P:存在语言A的判定器H 2)Q:存在以H为子程序的图灵机D(描述见上) 已知条件: 1)P→Q:如果有H,总能设计出D 2)┐Q:D是不存在的(证明见上) 证明: 1 P 假设 2 P→Q 已知条件 3 Q 1,2 4 ┐Q 已知条件 5 ┴ 推出矛盾 6 ┐P 假设不成立 上面的证明中,图灵机D的构造简直是神来之笔,图灵怎么想到的?虽然之前的证明没有直接给出不可判定的语言,但已经从数量上证明有图灵机不能判定的语言,由于判定器的要求更严格,所以可以推断所有判定器构成的集合小于所有语言构成的集合。这是个与“实数集的势大于自然数集”类似的命题,所以应该能用类似的方法——对角线方法证明。好,尝试一下。 康托构造映射表格时,表格的每一行由一个自然数表示这是第几行,每一列也由一个自然数标识列数,对角线法构造出来的实数实际上是一行,然而这一行却和每一行都不一样。刚才的证明我们看到,图灵机集合是可数集,可将其对应自然数,标识表格的每一行,那么每一列用什么标识呢?怎样让列数与行数相等呢?行和列的交叉处是什么呢?自然数/实数的例子中,每一行由一个自然数对应一个实数,在这个问题中,行由图灵机标识了,那么不难想到,每一行应该是一个语言。语言又该如何表示?下面依次回答这些问题。 列应该用什么来标识?在对角线方法中,表格的行列数一致,行和列都用自然数集标识。那么首先可以想到既然行用图灵机标识,那么列也可以用图灵机标识。但是这样的话行列交汇处就没什么意义了,试问随意挑选的两台图灵机之间能擦出什么火花? 脑子再转一下,图灵机与图灵机之间没有什么一般化的关系,图灵机识别的是语言,是字符串,那么将标识列的图灵机换成描述图灵机的串,既保持了行列数一致性,又让行列交汇处有了非平凡的意义!即,用M1, M2, M3.。.标识第1行、第2行、第3行„„再用描述图灵机的字符串《M1》, 《M2》, 《M3》。..标识第1列、第2列、第3列„„行列交汇处就填入accept或reject,表示一台图灵机是否接受描述某一台图灵机的串!这样,每一行刚好也就是一个语言,每一个部分的意义都正好是我们想要的。
《M1》
《M2》
《M3》
《M4》
„„
M1
accept
reject
reject
reject
M2
reject
reject
accept
M3
accept
accept
reject
accept
M4
reject
Accept
reject
accept
„„
为构造对角线准备的表格 走到这一步,离结果就很近了。 若将所有图灵机和描述它们的串排成表,行列交叉处就是H(Mi,《Mj》)的运行结果。构造图灵机D,实际上就是用对角线方法选出一行,这一行的第1列与M1相反,第2列与M2相反,第3列与M3相反„„所以构造出来的这一行肯定不在这个表中。如果在,这么D所在的行与对角线相交处会出现矛盾!
《M1》
《M2》
《M3》
《M4》
„„
D
„„
M1
accept
reject
reject
reject
accept
M2
reject
Reject
accept
reject
reject
M3
accept
Accept
Reject
accept
accept
M4
reject
accept
reject
accept
reject
„„
D
reject
accept
accept
reject
„„
D的每一列都与对角线相反,到它自己与对角线的交汇处产生矛盾 想必图灵深知语言集比图灵机集要“大”,一台图灵机只能对应一个语言,所以用对角线方法必定能构造出一个所有图灵机都不能识别的语言。这个语言就是D“识别”的语言,则D的语言肯定不会出现在那个图灵机和对应语言的表格中。如果强行将这台“不存在的图灵机”安插进表格中,必然产生矛盾,矛盾就发生在D所在行与对角线的相交处。就像康托用对角线方法构造出来的那个实数无法插入到[自然数-》实数]的映射表格中,否则构造出来的那个实数就与它自己矛盾了,神奇的“图灵机D”就是这么来的。 图灵是用图灵机的术语改写了对角线方法,在图灵机上重现康托的思想。
至此,回答了第一个问题:为什么图灵机也有不可判定的语言,并且还构造了一个这样的语言,即A={《M, ω》 | M描述一台图灵机,且M描述的机器接受ω},A又被称为接受问题。
语言A是超越图灵机极限的必然产物,因为图灵机和语言的内在关系决定了A这样不能被任何图灵机判定的语言是存在的。这是本质上的原因,但关于A本身还有一个表象上的原因(之前提到过):之所以不能用图灵机断定其它图灵机是否接受一个串,是因为图灵机不能断定其它图灵机在某个输入串上计算时是否会停机,这个问题同样是不可判定的,这就是著名的停机问题(Halting problem)。庄子曰,“吾生也有涯,而知也无涯,以有涯随无涯,殆已”。以有限的步骤去判定可能无限的计算,殆已。 但由此我产生了一个很大的疑问:为什么图灵机会不停机?这也是我试图回答的第二个问题。
 电子发烧友App
电子发烧友App































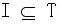













评论