- 无线传感器网络的低噪声放大器设计

为了得到最小的噪声系数, 源阻抗最佳值(最佳噪声源阻抗) Zop t应满足：

其中,α为共源管跨导与其源漏电导的比值。δ为一常数,γ为一系数, 在长沟道器件中,δ的值约为1. 33,γ的值约为0. 67, 在短沟道器件中, 这两个值都会因为短沟道效应而变大。定义c为栅噪声与漏噪声相关系数, 其值一般为0. 395 j, 为一纯虚数,反映了栅和沟道间噪声引起的的容性耦合程度。

源级电感Ls 和栅极电感Lg 不会导致最佳噪声源阻抗的实部发生变化,而仅对电抗部分产生影响。

要实现功率和噪声同时匹配,必须使输入阻抗Zin和最佳噪声源阻抗Zop t共轭匹配, 令Zin = 50 Ω,则有：

即：

式(6)中有4个方程, 4个未知数,只有一组解,即功率匹配和噪声匹配同时满足时, 功耗( Id )是确定的,不可以优化。而在限定功耗的情况下,功率匹配和噪声匹配则不可能同时满足。

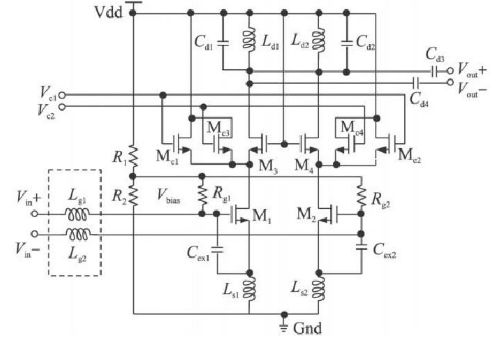
于是在电路设计中就需要在噪声匹配和功率匹配中进行折中。下面引入M1 管栅源间附加电容Cex ,这样,输入阻抗变为：

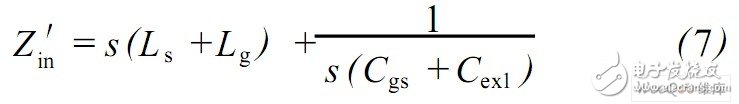
最佳噪声阻抗Z ′ op t表示为：

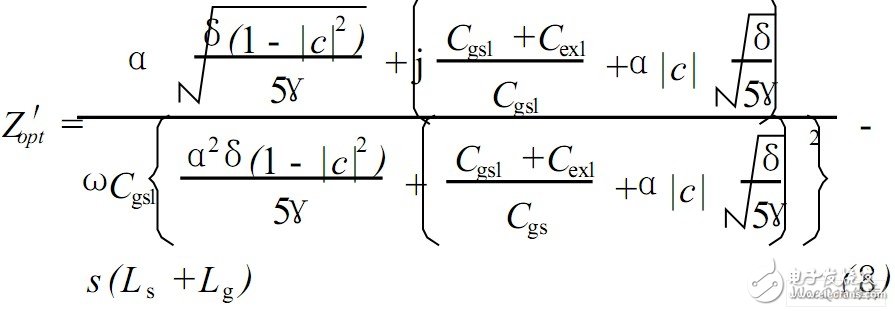
这样, 为了使功率和噪声同时匹配, 令Zin =Z ′ op t*= 50Ω,得到：

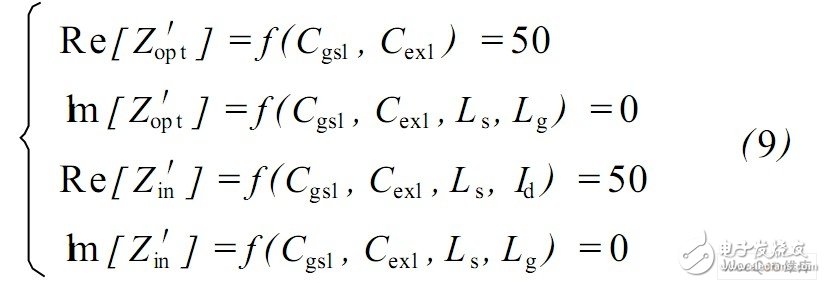
式( 9)中有4个方程, 5个未知数,则可以限定任何一个参数,再优化其它参数。所以,在功耗( Id )限定的情况下, 仍然可以进行功率噪声匹配。引入Cex后,通过调整Cex ,首先可以使最佳噪声源阻抗Z ′op t实部为50Ω。

再选择Ls ,使电路满足Re [ Z′in ] = Re [ Z ′op t ] =50Ω。根据式(8) 、式(9)可以推出：

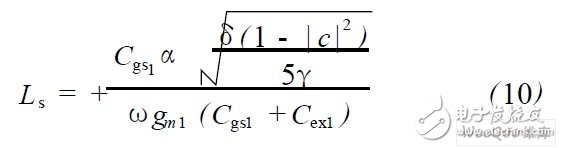
式(10)指出,选取的Ls 的电感值在引入Cex后亦可以比没有连接Cex时有所降低。Ls 为源极负反馈电感,由于电感中的寄生电阻影响以及该电感本身的负反馈性质,低感值的电感可以做到更好的噪声系数。

最后,调整片外电感Lg ,使谐振频率为ω0 (设计要求ω0 为2. 43 GHz) ,ω0 表示为：

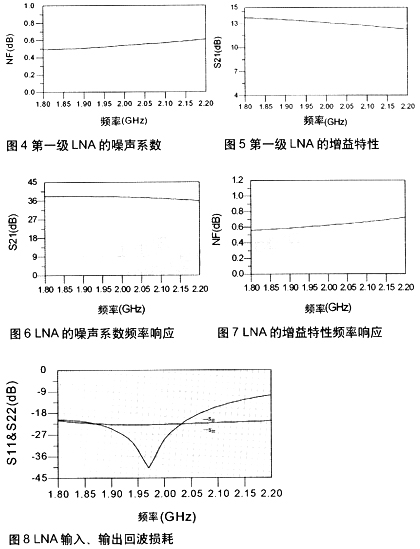
由于Cadence工具的局限性,仿真S参数时无法显示Sop t曲线,噪声匹配很难做到最优。在实际设计过程中,当共源管M1、M2 宽长比以及其偏置电路都已经确定时,可以通过扫描Cex参数,比较最小噪声系数NFmin ,选取其最佳值。当最小噪声系数NFmin确定后,再通过进一步调整Cex ,尽量满足功率匹配。在此过程中,必须同时关注噪声系数NF和最小噪声系数NFmin的变化,最后通过比较,选择折中的优化结果,确定恰当的Cex和Ls、Lg 值。

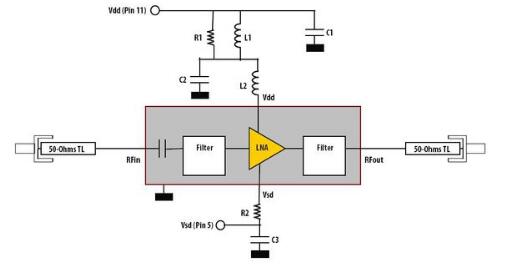
1. 3　输出匹配

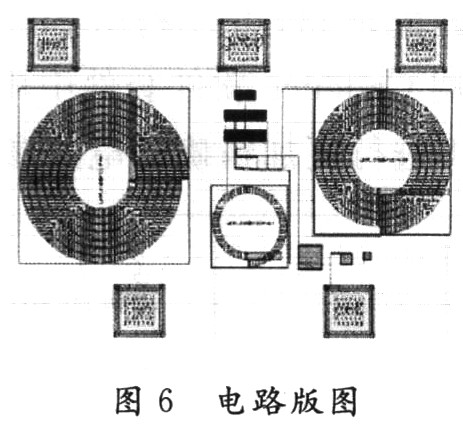
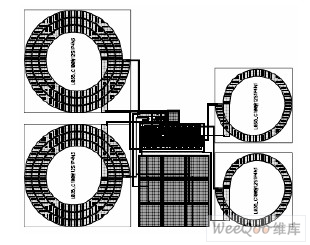
电路输出端通过漏极电感并联、串联电容的结构实现阻抗匹配。漏极电感的选取对低噪声放大器的性能有较大影响。电感值的大小直接影响放大器的增益。较大感值的电感可以增加LC并联谐振电路的等效阻抗,从而带来更高的电压增益。但是大电感的自谐振频率较低,而射频电路要求的工作频率却很高。同时,大电感也会占用更大的芯片面积,引入较大的噪声。而且,当电感值过大使放大器输出阻抗实部超过50Ω时,必需通过在输出端并联电感或增加源极跟随器等缓冲电路的方法才能将输出阻抗匹配到50Ω。如果直接并联电感,则会使输出端直流短路,要解决这个问题,则必须串联一个大电容后再将此电感并入电路,对于整体设计来说,引入了更多的无源元件,一方面大大影响了电路性能,另一方面也占用了更多面积。而增加一级缓冲电路,则会增加放大器的额外功耗。对于无线传感器网络节点中的模块,这两种方法都不可行。因此,具体设计时,需选取恰当的电感,既能保证应有的增益,又可以使输出阻抗实部在50Ω附近。