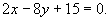2.1.1 导数的定义:设函数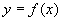 在点
在点 的某个邻域内有定义,当自变量
的某个邻域内有定义,当自变量 在
在 处取得增量
处取得增量
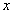 (点
(点 仍在该领域内)时,相应地函数
仍在该领域内)时,相应地函数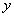 取得增量
取得增量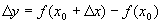 ;如果
;如果 与
与 之比当
之比当 时的极限存在,则称函数
时的极限存在,则称函数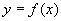 在
在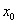 处可导,并称这个极限为函数
处可导,并称这个极限为函数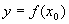 在点
在点 处的导数,记为
处的导数,记为 ,即
,即
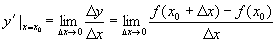 ,
,
也可记作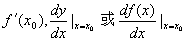 。
。
导数的定义式也可取不同的形式,常见的有
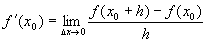 和
和
导数的概念就是函数变化率这一概念的精确描述。
2.1.2 求导举例
例 求函数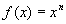 (n为正整数)在
(n为正整数)在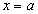 处的导数
处的导数
解 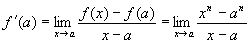
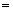
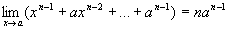
把以上结果中的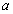 换成
换成 得
得 ,即
,即
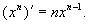
更一般地,对于幂函数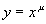 (
( 为常数),有
为常数),有
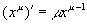
这就是幂函数的导数公式.
例 求函数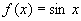 的导数
的导数
解 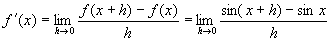
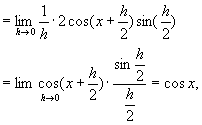
即 
这就是说,正弦函数的导数是余弦函数.
用类似的方法,可求得

就是说,余弦函数的导数是负的正弦函数。
例 求函数 的导数.
的导数.
解 
=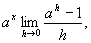
即
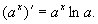
这就是指数函数的导数公式,特殊地,当 时,因
时,因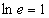 ,
,
故有 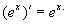
例 求函数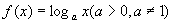 的导数.
的导数.
解 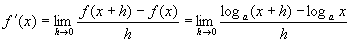

=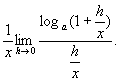
作代换
即得 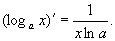
这就是对数函数的导数公式,特殊地,当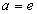 时,由上式得自然对数函数的导数公式:
时,由上式得自然对数函数的导数公式:
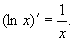
2.1.3 导数的几何意义
由导数的定义可知:函数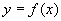 在点
在点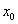 处的导数
处的导数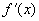 在几何上表示曲线
在几何上表示曲线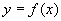 在点
在点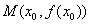 处的切线斜率,即
处的切线斜率,即
 ,
,
其中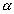 是切线的倾角.如下图:
是切线的倾角.如下图:

例 求等边双曲线 在点
在点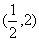 处的切线的斜率,并写出在该点处的切线方程和法线方程。
处的切线的斜率,并写出在该点处的切线方程和法线方程。
解 根据导数的几何意义知道,所求切线的斜率为
由于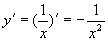 ,于是
,于是
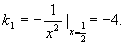
从而所求切线方程为
 即
即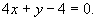
所求法线的斜率为
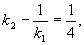
于是所求法线方程为