1.3.1 定义：若函数f(x)在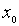
点的附近包括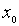点本身有定义，并且
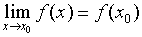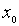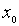，则称f(x)在点连续，为f(x)的连续点。
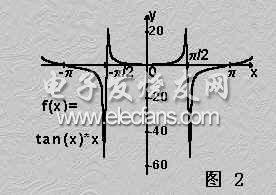
1.3.2 充要条件：f(x)在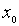点既是左连续又是右连续。
初等函数如三角、反三角函数，指数、对数函数等都是在自定义区间内的连续函数。
1.3.3 三类不连续点：
(1)第一类不连续点：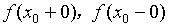
存在但不相等。
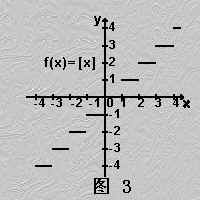
(2)第二类不连续点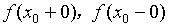：中至少有一个不存在。
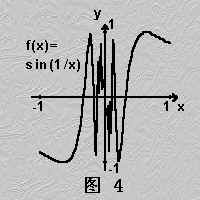
(3)第三类不连续点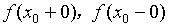：存在且相等，但它不等于
或f(x)在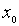点无定义。
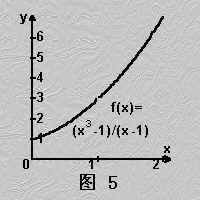
1.3.4 一致连续性的概念及它与连续的不同
1.7.1 定义：对
，可找到只与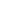
有关而与x无关的
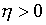，使得对区间内任意两点
，
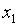，当
时总有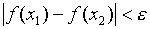
，就称f(x)在区间内一致连续。
1.7.2 与连续的比较：
(1)连续可对一点来讲，而一致连续必须以区间为对象。
(2)连续函数对于某一点
，
取决于和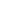，而一致连续函数的只取决于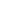，与x值无关。
(3)一致连续的函数必定连续。
[例：函数y = 1/x，当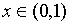
时非一致连续
当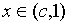
时一致连续]
(4)康托定理：
闭区间[a , b]上的连续函数f(x)一定在[a , b]上一致连续。