3.1.1 罗尔定理
罗尔定理 如果函数f(x)在闭区间[a , b]上连续,在开区间(a,b)内可导,且在区间端点的函数值相等,即f(a) = f(b),那么在(a,b)内至少有一点 ,使得函数f(x)在该点的导数等于零:
,使得函数f(x)在该点的导数等于零: 。
。
3.1.2 拉格朗日中值定理
拉格朗日中值定理 如果函数f(x)在区间[a,b]上连续,在开区间(a,b)内可导,那么在(a,b)内至少有一点 ,使等式
,使等式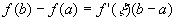 (1)
(1)
成立。
3.1.3 柯西中值定理
柯西中值定理 如果函数f(x)及F(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且F’(x)在(a,b)内的每一点处均不为零,那么在(a,b)内至少有一点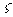 ,使等式
,使等式
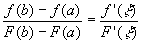 (2)
(2)
成立。
3.1.4.洛必达法则的概念.
定义:求待定型的方法(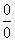 与此同时
与此同时 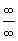 );
);
定理:若f(x)与g(x)在(a,a+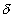 )上有定义,且
)上有定义,且 f(x)=
f(x)=  g(x)=0;
g(x)=0;
并且  与
与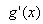 在(a,a+
在(a,a+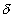 )上存在.
)上存在. 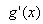
 0 且
0 且 
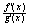 =A
=A
则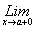
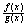 =
= 
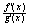 =A,(A可以是
=A,(A可以是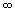 ).
).
证明思路: 补充定义x=a处f(x)=g(x)=0
则[a,a+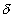 ) 上
) 上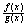 =
= =
=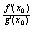
即 x 时,x
时,x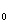
 ,于是
,于是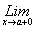
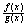 =
= 
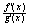
3.1.5 定理推广:由证明过程显然定理条件x 可推广到x
可推广到x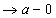 , x
, x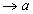 ,x
,x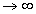 。所以对于
。所以对于 待定型,可利用定理将分子、分母同时求导后再求极限。
待定型,可利用定理将分子、分母同时求导后再求极限。
注意事项:
1.对于同一算式的计算中,定理可以重复多次使用。
2.当算式中出现Sin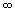 或Cos
或Cos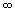 形式时,应慎重考虑是否符合洛必达法则条件中
形式时,应慎重考虑是否符合洛必达法则条件中 与
与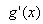 的存在性。
的存在性。
向其他待定型的推广。
1. 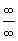 可化为
可化为 =
=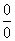 ,事实上可直接套用定理。
,事实上可直接套用定理。
2. 0
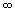 =0
=0
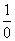
3. 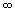 -
-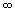 =
=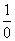 -
-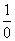 ,通分以后
,通分以后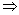
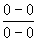 =
=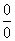 。
。
4. 、
、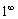 、
、 取对数
取对数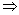 0
0 Ln0、
Ln0、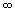
 Ln1、0
Ln1、0 Ln
Ln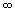
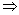 0
0
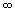 、
、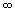
 0、0
0、0
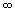 。
。
(注意:上述转化过程中描述引用的仅为记号.)
