3.2.1 泰勒公式及其误差图示
来源:实践,常用导数进行近似运算.
由于 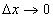 时
时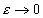 所以
所以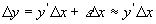
因此 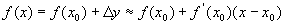
应用范围:常用以在直接求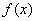 困难,而在
困难,而在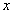 附近
附近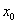 处
处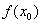 与
与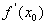 较易求得时应用.条件是
较易求得时应用.条件是 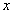 与
与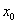 充分接近,即可达到一定的精度.
充分接近,即可达到一定的精度.
利用 当
当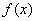 为不同函数时.
为不同函数时.
有常用近似公式如下:(|x|很小时)
3..2.2 函数图形描绘示例
定理:若f(x)在[a,b]上连续,(a,b)可导.则f(x)在[a,b]单调上升(或单调下降)的充分必要条件为(a,b)内![]() (或
(或![]() )
)
推论:若f(x)在[a,b]连续,(a,b)可导,且![]() 不变号
不变号
则![]() (或<0) 严格单调上升(下降).
(或<0) 严格单调上升(下降).
定理(极值的必要条件):若![]() 为f(x)的极值点,那么
为f(x)的极值点,那么![]() 只可能是
只可能是![]() 的零点或f(x)的不可导点.
的零点或f(x)的不可导点.
定理(极值判别法):![]() 则
则![]() f(
f(![]() )为极大值
)为极大值
![]() f(
f(![]() )为极小值
)为极小值
若![]() 不存在,但f(x) 在
不存在,但f(x) 在![]() 与
与![]() 上可导
上可导
则若![]() 内
内![]() ,
,![]() 内
内![]() 则 为极小点,反之为极大点
则 为极小点,反之为极大点
定义:若曲线在一点的一边为上凸,另一边为下凸,则称此点为拐点,显然拐点处![]()
定义:若![]() 则称ax+b为f(x)的一条渐进线.
则称ax+b为f(x)的一条渐进线.
定义:若![]() 则称x=c为f(x)的一条垂直渐进线.
则称x=c为f(x)的一条垂直渐进线.
定理:若f(x)的一条渐进线为ax+b 则![]() ,
,![]()
证明:由定义知![]() 即
即![]()
所以![]() 即
即![]() 带回定义得
带回定义得![]()
函数图象描述的基本步骤:
1.确定y=f(x)的定义域并讨论函数的基本性质,如奇偶性,对称性\周期性等.
2.求出![]() 与
与![]() 及
及![]() 与
与![]() 不存在的各点.
不存在的各点.
3.由2的结果函数的上升,下降区间,及图形的上凸,下凸区间以及各极值点.
4.定出函数的渐近线.
5.描点作用.
Sinx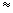 x,tgx
x,tgx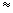 x,
x,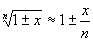 ,
,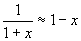 ,
,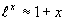 ,Ln(1+x)
,Ln(1+x)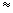 x.
x.
泰勒公式来源:上述公式在|x|很小时,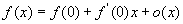 于是
于是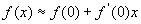 即,
即,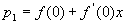 与
与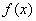 在x=0处函数值相等且,一阶导数相等.为进一步提高精度欲使
在x=0处函数值相等且,一阶导数相等.为进一步提高精度欲使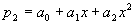 与
与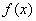 在二阶导数处也相等.于是
在二阶导数处也相等.于是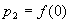 ,
,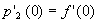 ,
,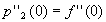 .
.
得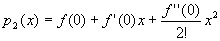
依此类推: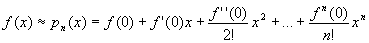
对于误差,有定理: 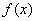 在x=0处有n+1阶连续导数,则上式误差
在x=0处有n+1阶连续导数,则上式误差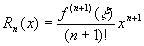 (
(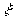 在x 与0 之间)
在x 与0 之间)
由定理: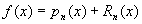 此式为
此式为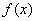 在x=0 处的关于x 的泰勒展开公式.即:
在x=0 处的关于x 的泰勒展开公式.即:
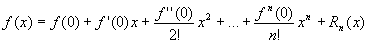
公式推广:一般地在x=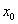 附近关于
附近关于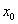 点的泰勒公式
点的泰勒公式

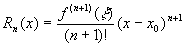
注意:虽然泰勒公式是在x=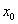 "附近"展开,但是事实上x可以取f(x)定义域内任意值,只不过若|x-
"附近"展开,但是事实上x可以取f(x)定义域内任意值,只不过若|x-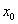 |过大(即x离
|过大(即x离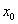 过远)时,
过远)时,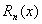 相应变大.即使用
相应变大.即使用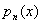 代替f(x)的误差变大.可是,无论如何泰勒公式总是成立的,当
代替f(x)的误差变大.可是,无论如何泰勒公式总是成立的,当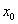 固定后,不同的x将使
固定后,不同的x将使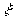 发生变化,并使
发生变化,并使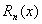 变化,从而影响
变化,从而影响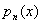 对f(x)的近似精度.
对f(x)的近似精度.
