5.1.1 定积分概念
定义 设函数f(x)在[a,b]上有界，在[a,b]中任意插入若干个分点
，
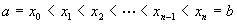把区间[a,b]分成n个小区间
，
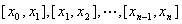设有常数I，如果对于任意给定的正数e ，总存在一个正数d ，使得对于区间[a,b]的任何分法，不论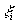
在
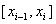中怎样取法，只要
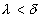，总有
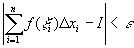
成立，则称I是f(x)在区间[a,b]上的定积分，记作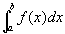 
。
接下来的问题是：函数f(x)在[a,b]上满足怎样的条件，f(x)在[a,b]上一定可积？以下给出两个充分条件。
定理1 设f(x)在区间[a,b]上连续，则f(x)在[a,b]上可积。
定理2 设f(x)在区间[a,b]上有界，且只有有限个间断点，则f(x)在[a,b]上可积。
如果我们对面积赋以正负号，在x轴上方的图形面积赋以正号，在x轴下方的图形面积赋以负号，则在一般情形下，定积分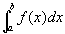的几何意义为：它是介于x轴、函数f(x)的图形及两条直线x = a、x = b之间的各部分面积的代数和。
5.1.2 牛顿－莱步尼兹公式及实例
定理 如果函数F(x)是连续函数f(x)在区间[a,b]上的一个原函数，则
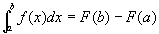。 (1)
证 已知函数F(x)是连续函数f(x)的一个原函数，又根据前面的定理知道，积分上限的函数
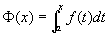
也是f(x)的一个原函数。于是这两个原函数之差为某个常数（第四章第一节），即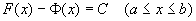 
。 (2)
在上式中令x = a，得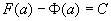
。又由F (x)的定义式及上节定积分的补充规定知F (a) = 0，因此，C = F(a)。以F(a)代入(2)式中的C，以
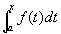代入(2)式中的F (x)，可得
，
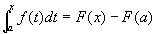在上式中令x = b，就得到所要证明的公式(1) 。n
由积分性质知，(1)式对a>b的情形同样成立。
为方便起见，以后把F(b) – F(a)记成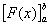
。
公式(1)叫做牛顿(Newton)-莱步尼兹(Leibniz)公式，它给定积分提供了一种有效而简便的计算方法，也称为微积分基本公式。
例1 计算定积分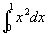
。
解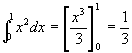 
。
例2 计算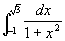
。
解 
。
例3 计算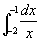
。
解 
。
例4 计算正弦曲线y = sinx在[0,p ]上与x轴所围成的平面图形的面积。
解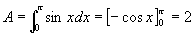 
。
例5 求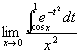
解 易知这是一个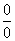
型的未定式，我们利用洛必达法则来计算。
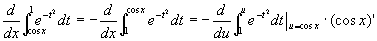
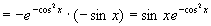
因此
。
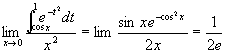