4.1.1 原函数与不定积分的概念
定义1 如果在区间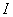 上,可导函数
上,可导函数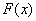 的导函数为
的导函数为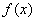 ,即对任一
,即对任一 ,都有
,都有
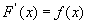 或
或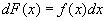 ,
,
那末函数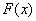 就称为
就称为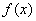 (或
(或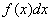 )在区间
)在区间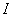 上的原函数。
上的原函数。
例如,因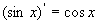 ,故
,故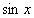 是
是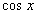 的原函数。
的原函数。
那一个函数具备何种条件,才能保证它的原函数一定存在呢?简单的说就是,连续的函数一定有原函数。
下面还要说明两点。
第一,如果有 ,那么,对任意常数C,显然也有
,那么,对任意常数C,显然也有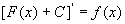 ,即如果
,即如果 是
是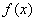 的原函数,那
的原函数,那
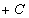 也是
也是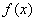 的原函数。
的原函数。
第二,当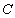 为任意常数时,表达式
为任意常数时,表达式
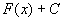
就可以表示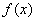 的任意一个原函数。也就是说,
的任意一个原函数。也就是说,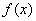 的全体原函数所组成的集合,就是函数族
的全体原函数所组成的集合,就是函数族
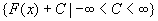 。
。
由以上两点说明,我们引入如下定义。
定义2 在区间 上,函数
上,函数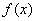 的带有任意常数项的原函数称为
的带有任意常数项的原函数称为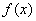 (或
(或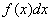 )在区间
)在区间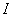 上的不定积分,记作
上的不定积分,记作
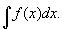 。
。
其中记号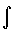 称为积分号,
称为积分号,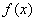 称为被积函数,
称为被积函数, 称为被积表达式,
称为被积表达式,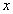 称为积分变量。
称为积分变量。
由此定义及前面的说明可知,如果 是
是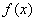 在区间
在区间 上的一个原函数,那么
上的一个原函数,那么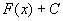 就是
就是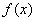 的不定积分,即
的不定积分,即
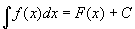 。
。
因而不定积分 可以表示
可以表示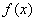 的任意一个原函数。
的任意一个原函数。
例 1 求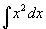 .
.
解 由于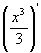 =
=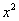 ,所以
,所以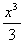 是
是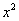 的一个原函数。因此
的一个原函数。因此
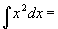
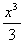
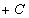 .
.
例 2 求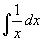 .
.
解 当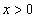 时,由于
时,由于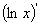 =
=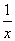 ,所以
,所以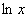 是
是 在
在 内的一个原函数。因此,在
内的一个原函数。因此,在 内,
内,
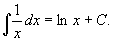
当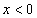 时,由于
时,由于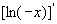 =
=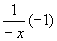 =
=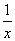 ,由上同理,在
,由上同理,在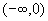 内,
内,
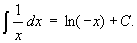
将结果合并起来,可写作

4.1.2 不定积分的性质
根据不定积分的定义,可以推得它的如下两个性质:
性质1 函数的和的不定积分等于各个函数的不定积分的和,即
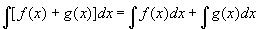 .
.
性质2 求不定积分时,被积函数中不为零的常数因子可以提到积分号外面来,即
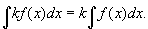 (
(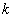 是常数,
是常数,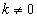 ).
).
例 3 求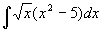 .
.
解 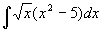 =
=
=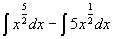
=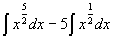
=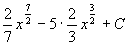
=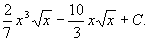
注意 检验积分结果是否正确,只要对结果求导,看它的导数是否等于被积函数,相等时结果是正确的,否则结果是错误的。
4.1.3 两类换元法及举例
利用基本积分表与积分的性质,所能计算的不定积分是非常有限的.因此,有必要进一步来研究不定积分的求法.
把复合函数的微分法反过来求不定积分,利用中间变量的代换,得到复合函数的积分法,称为换元积分法,简称换元法.
换元法通常分成两类.
第一类换元法
定理1 设f(u)具有原函数, u =φ(x)可导, 则有换元公式
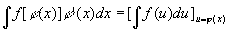
例1 求∫2cos2xdx.
解 作变换u=2x,便有
∫2cos2xdx =∫cos2x·2dx =∫cos2x·(2x)' dx =∫cos u du = sin u+C,
再以u=2x代入,即得
∫2cos2xdx =sin 2x+C.
例2 求∫tan x dx.
解 ∫tan x dx =∫sin x /cos x dx.
因为 -sin x dx = d cos x,所以如果设u=cos x,那么du=-sin xdx,即 -du=sin xdx,因此
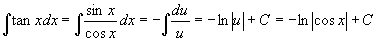 .
.
类似地可得∫cot x dx =ln|sin x|+C.
在对变量代换比较熟练以后,就不一定写出中间变量u.
例3 求∫ch(x/a) dx.
解 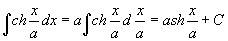 .
.
例4 求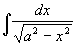 (a>0).
(a>0).
解 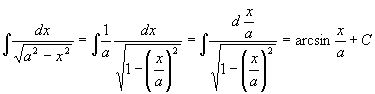 .
.
下面的一些求积分的例子,它们的被积函数中含有三角函数,在计算这种积分的过程中,往往要用到一些三角恒等式.
例5 求∫sin3 x dx.
解 ∫sin3x dx =∫sin2x sinx dx=-∫(1-cos2x)d(cosx)
=-∫d(cosx)+∫cos2xd(cosx)
=-cosx+(1/3)cos3x+C.
例6 求∫cos2 x dx.
解 
 .
.
类似地可得∫sin2 x dx=x/2-(sin2x)/4+C.
利用定理1来求不定积分,一般却比利用复合函数的求导法则求函数的导数要来的困难,因为其中需要一定的技巧,而且如何适当的选择变量代换u=φ(x)没有一般途径可循,因此要掌握换元法,除了熟悉一些典型的例子外,还要做较多的练习才行.
第二类换元法
定理2 设x=ψ(x)是单调的、可导的函数, 并且ψ'(x)≠0. 又设f[ψ(t)]ψ'(t)具有原函数,则有换元公式
 ,
,
其中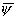 (x)是x=ψ(t)的反函数.
(x)是x=ψ(t)的反函数.
例7 求 (a>0)
(a>0)
解 求这个积分的困难在于有根式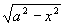 ,但我们可以利用三角公式sin2t+cos2t=1来化去根式.
,但我们可以利用三角公式sin2t+cos2t=1来化去根式.
设x=asint,-π/2<t<π/2,那么 ,于是根式化为了三角式,所求积分化为
,于是根式化为了三角式,所求积分化为
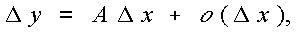 .
.
利用例6的结果得
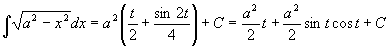 .
.
由于x=asint,-π/2<t<π/2,所以
 ,
,
于是所求积分为
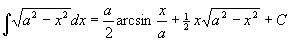 .
.
具体解题时要分析被积函数的具体情况,选取尽可能简捷的代换.
