6.2.1 曲面方程的概念及一般方程
如果曲面S与三元方程
F(x, y, z)=0 (1)
有下述关系：
-
曲面S上任一点的坐标都满足方程(1)；
-
不在曲面S上的点的坐标都不满足方程(1)，
那末，方程(1)就叫做曲面S的方程，而曲面S就叫做方程(1)的图形。
6.2.2 平面方程的几种形式
一般形式：
Ax+By+Cy+D=0，其中{A，B，C}是平面法向，
。
点法式方程：
。
截距式方程：
。
三点式方程：
已知平面过空间三点
，
，
，则平面方程为
-
几种特殊的曲面方程
-
旋转曲面方程
设平面曲线 l :
绕z轴旋转,则旋转曲线方程为 
-
柱面方程
母线平行与坐标轴的柱面方程为不完全的三元方程,如F(y, z)=0就表示母线平行与x轴,准线为
的柱面. -
二次曲面方程（见第七章知识点3）
6.2.3 空间曲线一般方程
空间曲线可以看作两个曲面的交线。设
F(x, y, z)=0 和 G(x, y, z)=0
是两个曲面的方程，它们的交线为C。
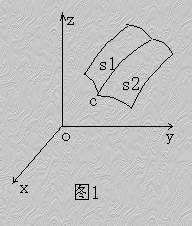
因为曲线C上的任何点的坐标应同时满足这两个曲面的方程，所以应满足方程组
（1）
反过来，如果点M不在曲线C上，那末它不可能同时在两个曲面上，所以它的坐标不满足方程组（1）。因此，曲线C可以用方程组（1）来表示。方程组（1）叫做空间曲线C的一般方程。
-
为空间曲线的一般方程，空间曲线的参数方程为
t为参数.
-
方程组
表示怎样的曲线?方程组中第一个方程表示母线平行于z轴的圆柱面,其准线是xOy面上的圆，圆心在原点O，半径为1。方程组中第二个方程表示一个母线平行于y轴的柱面，由于它的准线是zOx面上的直线，因此它是一个平面。方程组就表示上述平面与圆柱面的交线。
-
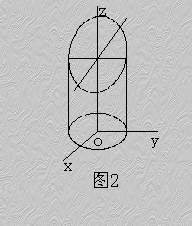
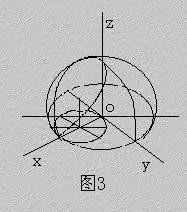
方程组
表示怎样的曲线？
方程组中第一个方程表示球心在坐标原点O ，半径为a的上半球面。第二个方程表示母线平行于z 轴的圆柱面，它的准线是xOy面上的圆，这圆的圆心在点（a/2，0），半径为a/2。方程组就表示上述半球面与圆柱面的交线。
6.2.4 空间曲线在坐标上的投影
设空间曲线C的一般方程为
由上述方程组消去变量z，x，y后所得的方程分别为：
H( x , y )=0 R( y , z )=0 T( x , z )=0
表示曲线C在xOy面上的投影,
表示曲线C在yOz面上的投影,
表示曲线C在xOz面上的投影。
例 已知两球面的方程为
（a） 和 
(b)
求它们的交线C在xOy面上的投影方程。
解 先求包含交线C而母线平行于z轴的柱面方程。因此要由方程(a) , (b)消去z，为此可先从（a）式减去(b) 式并化简，得到
y + z = 1
再以z = 1 –y 代入方程（a）或（b）即得所求的柱面方程为
容易看出，这就是交线C关于xOy面的投影柱面方程，于是两球面的交线在xOy面上的投影方程是
注：在重积分和曲线积分的计算中，往往需要确定一个立体或曲面在坐标面上的投影，这时要利用投影柱面和投影曲线。