7.1.1 多元函数的极限与连续性
设函数f(x,y)在开区域（或闭区域）D内有定义，P0(x0,y0)是D的内点或边界点。如果对于任意给定的正数ε，总存在正数δ，使得对于适合不等式
的一切点P(x,y)∈D,都有|f(x,y)-A|<ε成立，则称常数A为函数f(x,y)当 x→x0,y→y0时的极限，记作
或f(x,y) →A (ρ→0),这里ρ=|PP0|。
例 设
（x2+y2≠0），
求证
。
因为
，
可见，对任何ε>0，取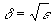
，则当
时，总有
成立，所以
。
我们必须注意，所谓二重极限存在，是指P（x,y）以任何方式趋于P0（x0,y0）时，函数都无限接近于A。
定义 设函数f(x,y)在开区域（或闭区域）D内有定义，P0(x0,y0)是D的内点或边界点且P0∈D。 如果
则称函数f(x,y)在点P0(x0,y0)连续。
7.1.2 性质
性质1（最大值和最小值定理） 在有界闭区域D上的多元连续函数，在D上一定有最小值和最大值。
性质2（介值定理） 在有界闭区域D上的多元连续函数，如果在D上取得两个不同的函数值，则它在D上取得介于这两个值之间的任何值至少一次。
一切多元初等函数在其定义区域内是连续的。所谓定义区域，是指包含在定义域内的区域或闭区域。
由多元初等函数的连续性，如果要求它在点P0处的极限，而该点又在此函数的定义区域内，则极限值就是函数在该点的函数值，即
。
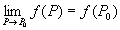7.1.3 偏导数的定义及计算法
设函数z=f(x,y)在点(x0,y0)的某一邻域内有定义，当y固定在y0而x在x0处有增量Δx时，相应的函数有增量f(x0+Δx,y0)-f(x0,y0),
如果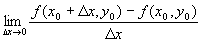
存在，则称此极限为函数z=f(x,y) 在点(x0,y0)处对x的偏导数，记作
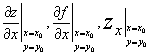或 fx（x0，y0）。
对于函数z=f(x,y)，求
时，只要把y暂时看作常量而对y求导。
例 求z=x2sin2y的偏导数。
解
。
7.1.4 高阶偏导数
定理 如果函数z=f（x,y）的两个二阶混合偏导数
在区域D内连续，那末在该区域内这两个二阶混合偏导数必相等。