7.3.1 空间曲线的切线与法平面
设空间曲线Г的参数方称为
x=φ(t),y=ψ(t),z=ω(t),
这里假定上式的三个函数都可导。[插图1]
插图1

插图2
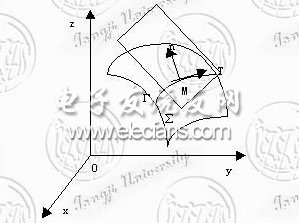
在曲线Г上取对应于t=t0的一点M(x0,y0,z0)。根据解析几何,可得曲线在点M处的切线方程为
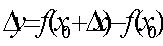 。
。
切线的方向向量称为曲线的切向量。向量
T={φ'(t0),ψ'(t0),ω'(t0)}
就是曲线Г在点M处的一个切向量。
通过点而与切线垂直的平面称为曲线Г在点M处的法平面,它是通过点M(x0,y0,z0)而以T为法向量的平面,因此这法平面的方程为
φ'(t0)(x-x0)+ψ'(t0)(y-y0)+ω'(t0)(z-z0)= 0。
7.3.2 曲面的切平面与法线(插图2)
设曲面Σ由方程F(x,y,z)= 0给出,M(x0,y0,z0)是曲面Σ上的一点,并设函数F(x,y,z)的偏导数在该点连续且不同时为零。则根据解析几何,可得曲面上通过点M的一切曲线在点M的切线都在同一个平面上。这个平面称为曲面Σ在点M的切平面。这切平面的方程是
Fx(x0,y0,z0)(x-x0)+Fy(x0,y0,z0)(y-y0)+Fz(x0,y0,z0)(z-z0)= 0
通过点M(x0,y0,z0)而垂直于切平面的直线称为曲面在该点的法线。法线方程是x=3
垂直于曲面上切平面的向量称为曲面的法向量。向量
n = {Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0)}
就是曲面Σ在点M处的一个法向量。
7.3.3 多元函数的极值
二元函数的极值问题,一般可以利用偏导数来解决。
定理1(必要条件) 设函数z = f(x,y)在点(x0,y0)具有偏导数,且在点(x0,y0)处有极值,则它在该点的偏导数必然为零:
fx(x0,y0) = 0,fy(x0,y0) = 0。
定理2(充分条件) 设函数z = f(x,y)在点(x0,y0)的某领域内连续且有一阶及二阶连续偏导数,又fx(x0,y0) = 0,fy(x0,y0) = 0,令
fxx(x0,y0) = A,fxy(x0,y0) = B,fyy(x0,y0) = C,
则f(x,y)在(x0,y0)处是否取得极值的条件如下:
(1)AC-B2>0时具有极值,且当A<0时有极大值,当A>0时有极小值;
(2)AC-B2<0时没有极值;
(2)AC-B2=0时可能有极值,也可能没有极值,还需另作讨论。
利用定理1、2,我们把具有二阶连续偏导数的函数z = f(x,y)的极值的求法叙述如下:
第一步 解方程组
fx(x,y) = 0,fy(x,y) = 0,
求得一切实数解,即可求得一切驻点。
第二步 对于每一个驻点(x0,y0),求出二阶偏导数的值A、B和C。
第三步 定出AC-B2的符号,按定理2的结论判定f(x0,y0)是否是极值、是极大值还是极小值。
7.3.4 条件极值 拉格朗日乘数法
拉格朗日乘数法 要找函数z = f(x,y)在附加条件φ(x,y) = 0下的可能极值点,可以先构成辅助函数
F(x,y)= f(x,y)+λφ(x,y) ,
其中λ为某一常数。求其对x与y的一阶偏导数,并使之为零,然后与方程φ(x,y) = 0联立起来:
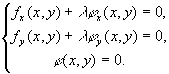
有这方程组解出x,y及λ,则其中x,y就是函数f(x,y)在附加条件φ(x,y) = 0下的可能极值点的坐标。
这方法还可以推广到自变量多于两个而条件多于一个的情形。
至于如何确定所求得的点是否极值点,在实际问题中往往可根据问题本身的性质来判定。
