8.1.1 二重积分的概念
为引出二重积分的概念，我们先来讨论两个实际问题。
设有一平面薄片占有xOy面上的闭区域D，它在点（x，y）处的面密度为ρ（x，y），这里ρ（x，y）> 0且在D上连续。现在要计算该薄片的质量M。
由于面密度ρ（x，y）是变量，薄片的质量不能直接用密度公式（M =ρS）来计算。但ρ（x，y）是连续的，利用积分的思想，把薄片分成许多小块后，只要小块所占的小闭区域D s i的直径很小，这些小块就可以近似地看作均匀薄片。在D s i（这小闭区域的面积也记作D s i
）上任取一点（x i，h i），则ρ（x i，h i）D s i（i = 1，2，…，n）可看作第i个小块的质量的近似值。（插图1）
插图1
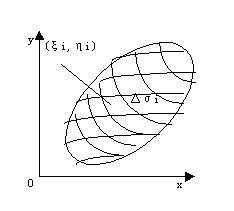
插图2
通过求和，再令n个小区域的直径中的最大值（记作λ）趋于零，取和的极限，便自然地得出薄片的质量M，即
。
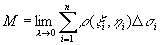再设有一立体，它的底是xOy面上的闭区域D，它的侧面是以D的边界曲线为准线而母线平行于z轴的柱面，它的顶是曲面z = f（x，y），这里f（x，y）≥ 0且在D上连续。这种立体叫做曲顶柱体。现在要计算上述曲顶柱体的体积V。
由于曲顶柱体的高f（x，y）是变量，它的体积不能直接用体积公式来计算。但仍可采用上面的思想方法，用一组曲线网把D分成n个小闭区域D s 1 ，D s 2，…，D s n，在每个D s i上任取一点（x i，h i），则f（x i，h i）D s i（i = 1，2，…，n）可看作以f（x i，h i）为高而底为D s i的平顶柱体的体积。（插图2）通过求和，取极限，便得出
。
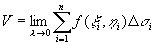上面两个问题所要求的，都归结为同一形式的和的极限。在其他学科中，由许多物理量和几何量也可归结为这一形式的和的极限。因此我们要一般地研究这种和的极限，并抽象出下述二重积分的定义。
定义 设f（x，y）是有界闭区域D上的有界函数。将闭区域D任意分成n个小闭区域
D s 1 ，D s 2，…，D s n，
其中D s i表示第i个小闭区域，也表示它的面积。在每个D s i上任取一点（x i，h i），作乘积 f（x i，h i）D s i（i = 1, 2, …, n,），并作和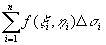
。如果当各小闭区域的直径中的最大值l 趋于零时，这和的极限总存在，则称此极限为函数f（x，y）在闭区域D上的二重积分，记作
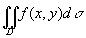，即
。（*）
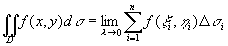其中f（x，y）叫做被积函数，f（x，y）ds 叫做被积表达式，ds 叫做面积元素，x与y叫做积分变量，D叫做积分区域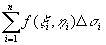，叫做积分和。
在二重积分的定义中对闭区域D的划分是任意的，如果在直角坐标系中用平行于坐标轴的直线网来划分D，那末除了包含边界点的一些小闭区域外，其余的小闭区域都是矩形闭区域。设矩形闭区域D s i的边长为D xj和D yk，则D s = D xj·D yk。因此在直角坐标系中，有时也把面积元素ds 记作dxdy，而把二重积分记作
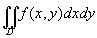
其中dxdy叫做直角坐标系中的面积元素。
这里我们要指出，当f（x，y）在闭区域D上连续时，（*）式右端的和的极限必定存在，也就是说，函数f（x，y）在D上的二重积分必定存在。
8.1.2 二重积分的性质
二重积分与定积分有类似的性质：
性质1 被积函数的常数因子可以提到二重积分号的外面，即
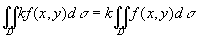（k为常数）。
性质2 函数的和（或差）的二重积分等于各个函数的二重积分的和（或差）。例如
。
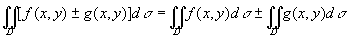性质3 如果闭区域D被有限条曲线分为有限个部分闭区域，则在D上的二重积分等于在各部分闭区域上的二重积分的和。例如D分为两个闭区域D1与 D2，则
。
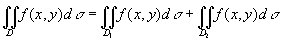此性质表示二重积分对于积分区域具有可加性。
性质4 如果在D上，f（x，y）= 1，s 为D的面积，则
。
此性质的几何意义很明显，因为高为1的平顶柱体的体积在数值上就等于柱体的底面积。
性质5 如果在D上，f（x，y）≤ j （x，y），则有不等式
。
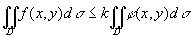特殊地，由于
- | f（x，y）| ≤ f（x，y）≤ | f（x，y）|，
又有不等式
。
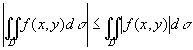性质6 设M，m分别是f（x，y）在闭区域D上的最大值和最小值，s 是D的面积，则有
。
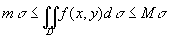上述不等式是对二重积分估值的不等式。
性质7（二重积分的中值定理） 设函数f（x，y）在闭区域D上连续，s 是D的面积，则在D上至少存在一点（x ，h ）使得下式成立：
。
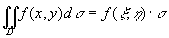