11.3 一阶线性微分方程
11.3.1 定义：
方程
（1）
叫做一阶线性微分方程，因为它对于未知函数y及其导数是一次方程。如果Q(x)＝0 则方程（1）称为齐次的；如果Q(x)不恒等于零，则方程（1）称为非齐次的。
11.3.2 非齐次线性方程的解法
在（1）中，如Q(x)≠0，我们先把Q(x)换成零而写出
（2）
方程（2）叫做对应于非齐次线性方程（1）的齐次线性方程。方程（2）是可分离变量的，分离变量后得
，
两端积分，得
，
或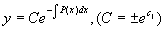 
，
这是对应的齐次线性方程（2）的通解。
现在我们用所谓常数变易法来求非齐次线性方程（1）的通解。把（2）的通解中的C换成x的未知函数u(x),即作变换
， （3）
于是 
.（4）
将（3）和（4）代入方程（1）得
即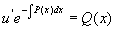
, 
两端积分，得 
把上式代入（3），便得非齐次线性方程（1）的通解
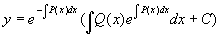. （5）
将（5）式改写成两项之和
第一项是对应的齐次线性方程（2）的通解，第二项是非齐次线性方程（1）的一个特解，由此可知，一阶非齐次线性方程的通解等于对应的齐次方程的通解与非齐次线性方程的一个特解之和。
例：求微分方程 
满足条件y(1)＝1 的特解。
解 先将方程化为线性方程标准形，再求解。
将原方程变形为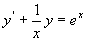
利用公式，
， 
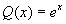
y
现由y(1)=1,得 C＝1，故方程的特解为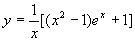
二．伯努利方程
方程
(10)
叫做伯努利（Bernoulli）方程.
当n=0或n=1时，这是线性微分方程。当n≠0或n≠1时，可把它化为线性的。只要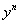
以除方程（10）的两端,得
。
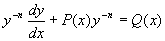容易看出，上式左端第一项与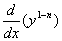
只差一个常数因1-n，因此我们引入新的未知函数
，那末
。
用(1-n)乘方程（11）的两端，再通过上述代换得线性方程
。
求出这方程的通解后，以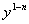 
代z，便得到伯努利方程的通解。